Title I-II OMB Part B 1-30-14
Title I-II OMB Part B 1-30-14.docx
Implementation of Title I/II Program Initiatives
OMB: 1850-0902
-
Implementation of Title I/II Program Initiatives
Supporting Statement for Paperwork Reduction Act Submission
PART B: Collection of Information Employing Statistical Methods
Contract ED-IES-11-C-0063
September 2013
(Updated January 2014)
Prepared for:
Institute of Education Sciences
U.S. Department of Education
Prepared by:
Westat
Mathematica Policy Research
.
Table of Contents
B.1. Respondent Universe and Sampling Methods 2
B.1.2. School District Sample 2
B.2. Information Collection Procedures 5
B.2.1. Notification of the sample, recruitment and data collection 5
B.2.2. Statistical Methodology for Stratification and Sample Selection 7
B.2.2.1. Nationally representative sample of school districts 7
B.2.2.2. Nationally representative sample of schools 11
B.2.2.3. Nationally representative sample of teachers 16
B.2.3. Estimation Procedures 21
B.2.4. Degree of Accuracy Needed 22
B.2.5. Unusual Problems Requiring Specialized Sampling Procedures 22
B.2.6. Use of Periodic (less than annual) Data Collection to Reduce Burden 23
B.3. Methods to Maximize Response Rates 23
B.3.1. Weighting the district, school, and teacher samples 23
B.5. Individuals Consulted on Statistical Aspects of Design 25
Appendix A State Survey and Extant Data Form A-1
Appendix B District Survey B-1
Appendix C Principal Survey C-1
Appendix D Teacher Survey D-1
Appendix E Teacher Roster E-1
Appendix F Notification Letters F-1
Appendix G Study Brochure G-1
Tables
B-1. Definitions of district size strata 8
B-2. Proposed stratification design for district sampling 9
B-3. Properties of proposed stratification design for district sampling 10
B-4. Proposed schools span-size subgroups for differential sampling rates 12
B-5. Subgroups for the school sample design 13
B-6. Expected school sample sizes for the subgroups in the school sample design 14
B-7. Power properties of school design 15
B-9. Expected teacher sample sizes 17
B-10. Effective sample sizes for national teacher estimates 18
B-13. Selected MDES for teachers by elementary, middle, and high school grade spans 21
Part B. Collection of Information Employing Statistical Methods
This package is the first of two for the Implementation of Title I/II Program Initiatives study. This package requests approval for an initial round of recruitment and data collection that will include surveys of all states, nationally representative samples of school districts and schools, and a nationally representative sample of Kindergarten through 12th grade teachers who teach core academic subjects and special education.1 We anticipate that the state education agency (SEA), school district principal, and teacher surveys will begin in February 2014. The second package will request approval for the follow-up survey, which will survey the same states, districts, and schools as well as a new nationally representative sample of teachers within the sampled schools.
Introduction
Title
I is one of the U.S. Department of Education’s (ED) largest
elementary and secondary education programs. Historically, Title I
provides financial assistance to schools and districts with a high
percentage of students from low-income families to help these
students increase achievement. Title I also includes requirements
that states hold schools and districts accountable for improvements
in student achievement. During the 2009-2010 school year, more than
56,000 public schools used Title I funds, and the program served 21
million children (U.S. Department of Education, 2012a). Title II
provides funds to increase academic achievement by improving teacher
and principal quality including educator preparation and professional
development, as well as providing funds for class size reduction. An
estimated 95 percent of districts nationally received Title II, Part
A funding for the 2011-12 school year (U.S. Department of Education,
2012b).
The last National Assessment of the Title I program concluded in 2006. Since that time, there have been changes in Title I provisions, such as allowing states to incorporate proficiency improvement (alongside proficiency levels) into school accountability measures and providing more resources to the lowest performing schools through the expansion of eligibility and funding for School Improvement Grants (SIG). Title II guidance allows more flexibility for certain teachers (e.g., special education teachers) to meet the standards to become highly qualified teachers (HQT).
The most recent change related to Title I and Title II was the introduction of the Elementary and Secondary Education Act (ESEA) Flexibility requests in 2011, allowing states to waive a number of provisions in exchange for a commitment to key reform principles. The Title I/II study will provide policy makers with detailed information on how these initiatives are playing out in states, districts, schools, and classrooms.
Overview of the Study
The
Implementation of Title I/II Program Initiatives study is
commissioned by the Institute of Education Sciences (IES), ED’s
independent research and evaluation arm. The Title I/II study will
examine the implementation of policies promoted through ESEA at the
state, district, school, and classroom levels. Through surveys at
each level and selected extant data and documents, the study will
provide information on activities in four core areas: state content
standards, assessments, school accountability, and teacher and
principal evaluation.
The study will reflect changes in Title I and Title II provisions since the last National Assessment of the Title I program concluded in 2006 (including ESEA Flexibility provided to states with approved requests). In addition, this study will supplement findings from ED’s annual survey of a nationally representative sample of districts on their uses of Title II, Part A funds. This study will provide more detail on district-implemented workforce development policies and practices for educators as well as teachers’ and principals’ access to and receipt of professional development.
B.1. Respondent Universe and Sampling Methods
The
study sample will include the universe of states and the District of
Columbia, and nationally representative samples of districts and
schools. The study also includes a nationally representative sample
of Kindergarten through 12th
grade teachers who teach core academic subjects and special
education. These are teachers whose
subject most often taught
is reading/English/language arts, mathematics, science, social
studies, general elementary, or special education. The
school sample will be nested in the district sample, and the teacher
sample will be nested in the school sample.
B.1.1. State Sample
We will survey all 50 states and the District of Columbia.
B.1.2. School District Sample
A nationally representative sample of districts will be selected. This will provide unbiased estimators of district characteristics, and will provide the first stage of selection for samples of schools and teachers. A nationally representative sample is necessary as Title I/II covers most of the U.S. public school educational system.
We also are interested in statistically comparing the implementation of initiatives promoted by Title I and Title II by district level of poverty and size of districts based on student enrollment. Poverty is included because Title I is specifically intended to ameliorate the effects of poverty on local funding constraints and education opportunity. District capacity to implement initiatives also will be of interest for this study. Success in implementation of initiatives, particularly those that build upon each other such as having longitudinal data systems and identifying effective teachers, might be tied to district organizational capacity. Therefore, we also will examine implementation by district size.
For the district sample, we will implement a “minimax” sample design that strikes a balance between producing efficient student-weighted estimates and efficient district-weighted estimates. This seems appropriate because the policy levers of Title I and Title II are directed at districts (and schools and states). For some purposes, it will be useful to understand the average experience of students across the country, but for other purposes, we will want to understand the experience and behavior of the average districts (and schools)—the units that the U.S. Department of Education (ED) expects its policies to immediately influence. The minimax design is a compromise between a design that is relatively efficient (i.e., allows estimates with narrow confidence intervals) for answering questions about the number or proportion of U.S. public school students in districts implementing initiatives of interest, and one that is relatively efficient for answering questions about the number or proportion of U.S. school districts implementing such initiatives.2
To construct the sampling frame, we will use data primarily from the National Center for Education Statistics’ (NCES) Common Core of Data (CCD), with supplementary data from sources such as the U.S. Bureau of the Census’s district-level SAIPE (Small Area Income and Poverty Estimates) program for school-district percentages of families with children in poverty.
We will draw a district sample of 570 districts out of 15,762 school districts. See Table B-2 in Section B.2 for the universe counts by stratification classifications.
B.1.3. School Sample
A nationally representative sample of schools will be selected. The school sample will be a two-stage sample, nested within the sampled districts. This will provide unbiased estimators of school characteristics, and will provide the second stage of selection for a sample of teachers who teach core academic subjects and special education.
In addition to examining initiatives in schools nationwide, we also will statistically compare policy implementation by school Title I status, school poverty level, and the cross-classification of Title I and poverty status (high-poverty Title I schools, low-/medium-poverty Title I schools, and non-Title I schools).3 The school sample is not limited to Title I schools. While a key part of the study focuses on initiatives promoted by Title I, the study is not looking exclusively at initiatives funded by Title I. Furthermore, non-Title I schools may benefit from professional development funded by district Title II funds. In addition, we anticipate that implementation status and types of initiatives may vary by school grade span (elementary, middle, and high schools). For example, implementation of state content standards and aligned assessments, as well as responses to accountability systems, likely differs by grade level. As a result, we will look for differences between Title I and non-Title I schools within grade span. There is variation in the poverty levels of Title I schools, with 33.3% percent of Title I schools considered high-poverty schools.4 Our analysis will examine whether implementation of initiatives is different in the neediest Title I schools
We will also implement a “minimax” sample design for the school sample. This will balance between the needs to produce efficient student-weighted estimates and efficient school-weighted estimates. To construct the sampling frame, we will use data from the CCD.
We will draw a sample of 1,300 schools nested within the nationally representative sample of 570 school districts. (The universe of schools is 92,149 schools.) See Table B-5 in section B.2.2.3 for the universe counts by stratification classification.
B.1.4. Teacher Sample
A nationally representative sample of teachers who teach core academic subjects and special education will be selected. In limiting the sample to these types of teachers, the sample will include teachers most likely to be affected by the various initiatives and programs promoted by Title I and the ESEA Flexibility waivers. In addition, we believe there will be considerable interest in the responses of teachers who teach any classes in which students are tested for accountability requirements for ESEA 5 as they have been the focus of the federal accountability system. These teachers also are most likely to be affected by improved measures of educator effectiveness based on student growth. Teachers in these subjects and grades are also the most likely to be affected by state-set achievable annual measurable objectives (AMOs) promoted by the ESEA Flexibility requests, and will most likely receive student growth data for use in improving practice and differentiating instruction (U.S. Department of Education, 2011). By including all teachers of core academic subjects, the study can compare the experiences of teachers whose students are tested for ESEA accountability with experiences from teachers of other comparable core subjects who are not as likely to be directly affected by these policies.
The sample will thus allow statistical comparisons of ESEA-tested and non-ESEA-tested teachers by school grade span on such topics as teachers’ use of student achievement, and especially growth in achievement, for evaluation, accountability, and practice improvement.6 Special education teachers are included in the sample because they are also expected to teach core subjects to students who are an important subgroup in both ESEA accountability measures and the states AMOs under ESEA Flexibility waivers.
The teacher sample will be a three-stage sample, nested within sampled districts and schools. This will provide unbiased estimators of teacher characteristics. The sample will be drawn from a comprehensive list of teachers who teach core academic subjects and special education provided to us from each sampled school. 7
Our sample will include sufficient numbers of teachers per district and school to allow examination of the relationship between implementation of various initiatives promoted by Title I and Title II as described by principals and district officials and teachers’ reports of their experiences and responses. For example, we may examine whether teachers in states that provide more extensive support for state content standards are more likely to report using the state content standards in their classrooms than teachers in other states.
The study will use an approach similar to the teacher sampling in the NCES Schools and Staffing Survey (SASS) to determine the overall number of teachers to select from each sampled school. In general, the SASS approach sets a teacher sample size for each sampled school using the teacher roster count from the school and the school’s probability of selection, in such a way that yields a “self-weighting” sample (each teacher of core academic subjects or special education in each school has an equal probability of selection within the three major school subgroups (non-Title I, Title I high poverty, Title I low poverty)). Effectively, the teacher sample size is selected in a way that cancels out any oversampling or undersampling of the school given its teacher count, bringing the teacher probabilities back to equality across schools within each major school subgroup, to the extent possible. This avoids large differences in the weight given to individual teachers, differences which complicate estimating standard errors and can reduce stability of estimates.
We will draw a sample of 9,100 teachers of core academic subjects and special education from the 1,300 sampled schools—an average of seven teachers per sampled school. See Table B-9 in Section B.2 for the expected teacher sample sizes by school classification.
We expect all states and the District of Columbia to participate in the study. We expect to obtain at least an 85 percent response rate from districts, schools, and teachers.
B.2. Information Collection Procedures
B.2.1. Notification
of the sample, recruitment and data collection
Introduce the Study to State Education Agencies. We will begin by sending the chief state school officer and the state Title I administrator a notification letter (see Appendix F) and study brochure (see Appendix G) explaining the study, the importance of the state’s involvement, and the mandatory nature of the state’s response. We will then follow up with a phone call to the state Title I administrator to answer questions about the study and identify additional state-level respondents based on areas of expertise. Once we have secured the correct contacts, we will mail the Title I administrator a hard copy instrument with instructions to have other staff complete relevant sections.8
The mailing will include a version of the extant data form that will be pre-filled with the data that we have collected from publicly available sources. We will ask the respondents to review the form to confirm the accuracy of the data, correct any data that were not correct on the public website, and provide any data that were not available publicly.
The mailing will include a password and secure web address to access an electronic version of the questionnaire and instructions on how to submit the questionnaire via a secure SharePoint site. After the initial mailing, we will also send a follow-up email that also includes the web address and password. Project staff will monitor completion rates, review the instruments for completeness throughout the field period, and follow up by email and telephone as needed to answer questions and encourage completion. During these calls, state representatives will be given the option of completing the module by telephone with the researcher. Each of the four topic areas (state content standards, assessments, accountability and low-performing schools, and teacher and principal evaluation) will on average require between 30 and 45 minutes to complete.
Researchers knowledgeable about the four content areas will review the completed questionnaire and documentation downloaded from state and other publicly available web sites for completeness. We will then conduct follow up calls with states to clarify any ambiguous answers in the survey.
Introduce the Study to District and School Leaders. We will send notification letters (see Appendix F) and the study brochure (see Appendix G) by email and mail to sampled districts and schools. Notification letters will be customized for each type of respondent, informing them of the study’s importance and benefits. Sending both email and mail will increase the likelihood that addressees will receive our communications in a timely manner. States and districts receiving Title I and Title II funds have an obligation to participate in Department evaluations (Education Department General Administrative Regulations (EDGAR) (34 C.F.R. § 76.591)), and virtually all states and districts receive Title I and/or Title II funds. Since we are not able to discern which schools receive Title I and/or Title II funds, survey participation is not mandatory for school principals.
Mailings to district superintendents will include the names of the sampled schools. Because we anticipate that district surveys will require input from several key individuals, we will ask the district superintendent to provide contact information (including email) for a person designated by the superintendent as the study liaison, who will coordinate the completion of the survey by the appropriate staff. Once the district liaison is identified, we will conduct all follow-up directly with the district liaison.
For those districts that do not respond and identify a study liaison online within five days, we will make follow-up telephone calls to district superintendents to confirm receipt of the letter, answer any questions, confirm the identity of the study liaison, and obtain the designated liaison’s contact information. We will follow all required procedures, and as necessary, we will obtain the approval of the district for principal and teacher participation through submission of the required research application. Notification letters will not be sent to principals or teachers prior to district approval.
Principal mailings will begin once we have received any required district approval. The principal mailings will inform principals of their schools’ selection and also will include directions for completing the teacher roster via the web from which we will draw the teacher sample. Principals will be asked to verify their schools’ current grade spans and list all current teachers whose subject most often taught is reading/English/language arts, mathematics, science, social studies, general elementary, or special education. For each of these teachers, the school will identify the subject most often taught, the main grade for the subject most often taught, and whether the teacher teaches any class whose students are tested for accountability requirements under ESEA. Mockups of web pages that could be used to collect this information are shown in Appendix E.
Online edits in the web roster will ensure that all data items required for teacher sampling are entered. The principal mailing will include a hardcopy roster listing all of these items and a fax number and business reply envelope, should school staff prefer to submit hardcopy. We will also make available at the school’s request an Excel template should the school staff prefer to enter teacher information in Excel. We will also accept roster output from the school’s database, either electronically or on hardcopy. We will work with the principal or his/her designee to be sure all fields required for teacher sampling are captured. As teachers are selected from a school, we will identify their email addresses from the school’s web site, and email their notification letters.
Administer Surveys. By email and mail, we will send a notification letter to all respondents (i.e., school principals, and teachers). The letters and emails will underscore the purpose of the study and the importance of participation. Letters and emails will be tailored to the respondents with the district communication informing district-level respondents that completing the web-based survey is mandatory and required by law. Principals will be informed that their participation is voluntary and they will receive $25 as a thank you for their participation. We will emphasize that the survey is an opportunity for principals and teachers to provide valuable information about how the policies of ESEA influence teaching and learning. Teachers also will be informed that their participation is voluntary and that they will receive $20 as a thank-you for their participation. In districts that require research applications for principal and teacher participation, we will send the principal and teacher emails once we obtain district approval to begin data collection. Mailed letters will include the survey URL and login information for responding to the survey as a web-based instrument. For security purposes, the first email will provide the URL and the User ID with the respondent’s password provided in a second email.
All communications will include a toll-free study number and a study email address for respondents’ questions and technical support. Based on Westat’s experience on large-scale data collections, we will assign several trained research staff to answer the study hotline and reply to emails in the study mailbox. We will train them on the purpose of the study, the obligations of district respondents to participate in the evaluation, and the details for completing the web-based survey. Content questions will be referred to the study leadership. An internal FAQ document will be developed and updated as needed throughout the course of data collection to ensure that the research staff has the most current information on the study.
The web will be our primary method of data collection for the district, school and teacher surveys. We will offer respondents the option of emailing them an electronic version of the survey (e.g., PDF or Word document) to complete and return by email or completing a paper-and-pencil instrument. However, we have found that the vast majority of respondents in districts and schools prefer the web-based approach. A phone survey option will be offered to respondents as part of the nonresponse follow-up effort. Since the web-based surveys will include data checks, we will use the web-based surveys to enter any surveys received on hard copy or by phone.
Westat will develop a web-based data monitoring system (DMS) to track the sample for each instrument, record the status of district approvals, generate materials for mailings, and monitor survey response rates.
B.2.2. Statistical Methodology for Stratification and Sample Selection
B.2.2.1. Nationally representative sample of school districts
The district sample will be stratified by poverty status and district size. The poverty strata are defined based on the percent of families with children in poverty. The high-poverty stratum consists of the roughly 25 percent of districts with percentages greater than the national 75th percentile.9 The low/medium-poverty stratum consists of the complement set (roughly 75 percent of the districts). The district size strata are given in Table B-1. It should be noted that for comparing adjacent classes, each class has an enrollment range roughly three times greater than the preceding class (in terms of minimums, mean value, or maximums).
Table B-1. Definitions of district size strata
District oversampling class |
Lower bound district enrollment |
Upper bound district enrollment |
G |
1 |
500 |
F |
501 |
1,500 |
E |
1,501 |
5,000 |
D |
5,001 |
15,000 |
C |
15,001 |
50,000 |
B |
50,001 |
150,000 |
A |
150,001 |
no limit |
A total of 570 districts will be sampled, with oversampling of high-poverty districts by a factor of 3. This oversampling will bring the expected sample size for high-poverty districts in line with the expected sample size for low/medium-poverty districts.
Table B-2 presents the proposed strata for sampling districts, with relative sampling rates (as compared to the stratum with the lowest sampling rate). The counts are based on the 2011-12 school-year CCD frame. Note that under a probability proportionate to size by enrollment design, the relative sampling rates between neighboring district size classes would be 3, as that is roughly the enrollment ratio. By using powers of 1.80 rather than powers of 3 as relative sampling factors, we are oversampling the strata with the higher enrollments, but not to the full extent justified by the ratios of enrollment means. The largest eight low/medium-poverty stratum and the largest 6 high-poverty stratum districts are sampled with certainty (indicated with a relative sampling rate of infinity). The exceptionally large size of these districts will make them larger than the sampling interval under the minimax design (described below), and they will be taken as certainties to maintain efficiency.
Table B-2. Proposed stratification design for district sampling
Poverty stratum |
District size class |
District count |
Percent of districts |
Relative sampling rate |
Expected district sample size |
Percent of district sample |
Low/med |
G |
3,955 |
25.1% |
1.00 |
36.2 |
6.4% |
Low/med |
F |
3,431 |
21.8% |
1.80 |
56.6 |
9.9% |
Low/med |
E |
3,062 |
19.4% |
3.24 |
90.9 |
16.0% |
Low/med |
D |
1,115 |
7.1% |
5.83 |
59.6 |
10.5% |
Low/med |
C |
346 |
2.2% |
10.50 |
33.3 |
5.8% |
Low/med |
B |
59 |
0.4% |
18.90 |
10.2 |
1.8% |
Low/med |
A |
8 |
0.1% |
Inf |
8.0 |
1.4% |
Low/med |
Total |
11,976 |
76.0% |
|
295 |
51.8% |
High |
G |
1,686 |
10.7% |
3.00 |
51.5 |
9.0% |
High |
F |
948 |
6.0% |
5.40 |
52.1 |
9.1% |
High |
E |
764 |
4.8% |
9.72 |
75.6 |
13.3% |
High |
D |
265 |
1.7% |
17.50 |
47.2 |
8.3% |
High |
C |
98 |
0.6% |
31.49 |
31.4 |
5.5% |
High |
B |
19 |
0.1% |
56.69 |
11.0 |
1.9% |
High |
A |
6 |
0.0% |
Inf |
6.0 |
1.1% |
High |
Total |
3,786 |
24.0% |
|
275 |
48.2% |
Total |
Total |
15,762 |
100.0% |
|
570 |
100.0% |
This sample design we call a ‘minimax’ design, as it is designed to equalize the efficiency for two types of estimates. The first type of estimate counts each district as one in the population, so that the base weight is the inverse of the district probability of selection. This type of ‘count-based’ estimate answers questions such as “What percentage of districts have characteristic X?” The second type of estimates includes enrollment of the district, so that the sampling base weight is the enrollment divided by the probability of selection. This type of ‘enrollment-based’ estimate answers questions such as “What percentage of students are enrolled in districts which have characteristic X?” A probability proportionate to enrollment design will lead to optimal efficiency for the second type of estimate, but will have poor efficiency for the first type of estimate (as the district weights will be close to equality for the enrollment-based estimate, but will vary considerably for the count-based estimate). On the other hand, a simple stratified design with no oversampling of larger district-size strata will have high efficiency for count-based estimates, but poor efficiency for enrollment-based estimates. This ‘middle-ground’ design oversamples the higher enrollment district-size strata, but proportional to the 0.535 root10 of the enrollment mean in the stratum, rather than to enrollment directly,11 and will have reasonable efficiency for both count-based estimates and enrollment-based estimates (the design is set up to equalize the efficiency for both types of estimates, at the cost of not being as good for each type of estimate as the optimal design for that type of estimate). Table B-3 summarizes the properties of this design.12
Table B-3. Properties of proposed stratification design for district sampling
Power Property |
Enrollment-based weight estimates |
Count-based weight estimates |
|
|
|
Effective sample size: All districts |
294.6 |
292.4 |
Effective sample size: High-poverty districts |
237.7 |
174.8 |
Effective sample size: Low/medium-poverty districts |
179.6 |
186.9 |
Minimum detectable effect size (MDES) comparing Poverty District Strata |
27.7% |
29.5% |
The effective sample sizes are the sample sizes for a simple random sample which would provide the same precision as the design.13 Note that the effective sample size for all-district estimates is about half of the district sample size of 570. This large ratio is caused partially by the oversampling of high-poverty districts. Note also an equalization of effective sample sizes for the two types of estimates. This is the ‘minimax’ aspect. The MDES (minimum detectable effect size) is computed for evaluating the null hypothesis of no difference between the high-poverty and the low/medium-poverty districts for a range of district-level characteristics.14 This is a very important comparison at the district level for this study, and the sample design is carefully tailored with this comparison in mind (we effectively equate the sample designs for the two strata, though the high-poverty districts are only one quarter of enrollment). The sample design does achieve an MDES lower than 30 percent for both types of estimates.15
The district frame is based on the 2011-12 CCD frame, as processed through National Assessment of Educational Progress (NAEP) macros to purge entities that are not in scope (e.g., administrative districts, district consortiums, entities devoted to auxiliary educational services, etc.), as well as a canvassing of new districts from the preliminary CCD frame from the following year (only districts with positive enrollments on the CCD frame, with other out-of-scope entities purged out). All school districts and independent charter districts with at least one eligible school and at least one enrolled student will be included in the frame.16
Further Details of District Sampling. The primary strata are by district-size class and poverty status as described in the previous section. We also plan to define a stratum for small states (states with an expected district sample size less than 1), and carry out a systematic sample within this stratum by state in order to guarantee that every state has at least one selected district. The remaining complement stratum will be stratified by poverty status (high and medium/low) and district-size class as described above. Within these primary strata, there will be further implicit stratification by ordering the sample. This ordering will be defined by urbanicity, Census region, and finally district enrollment.
The high-poverty stratum will be formally defined by SAIPE estimates of percentages of 5 to 17 year old children in poverty for the school district. We will compute the weighted 75th percentile percentage over all districts in the U.S., and the mean value will become the cutoff. Districts with percentages lower than the cutoff will be designated ‘low/medium-poverty’ and districts with percentages higher than the cutoff will be designated ‘high poverty.’ Independent districts such as charter school districts will be associated with the public school district that they are associated with geographically, as only the primary geographically-based public school districts have poverty estimates from SAIPE.
Any districts with only one school will have a sampling rate set to be 1/4 of the sampling rate they would otherwise receive. Even with this undersampling, they will still be represented correctly in the population, as their weights will reflect their reduced probabilities of selection (the weights will be four times larger than they would otherwise be), but we will have fewer of these districts. This method of undersampling is similar to that done in the NAEP for schools with very small numbers of students.
B.2.2.2. Nationally representative sample of schools
The school sample is a two-stage sample of 1,300 schools, nesting within the sampled districts. There will be sampling rates assigned for sampling groups defined by school Title I status,17 school poverty status, and by school span and school size. Table B-4 presents the proposed 10 span-size subgroups with differential sampling rates.
School grade span is defined as follows, following the CCD definition:
elementary is defined to have a low grade of Pre-K through 3rd grade, and a high grade of Pre-K through 8th grade;
middle is defined to have a low grade of 4th through 7th grade, and a high grade of 4th through 9th grade;
high school is defined to have a low grade of 7th through 12th, and a high grade of 12th only; and
other schools is defined to include all other schools.
Table B-4. Proposed school span-size subgroups for differential sampling rates
School span |
School size class |
School count |
Percent of schools |
Enrollment |
Percent of enroll-ment |
Minimum enroll-ment |
Maximum enroll-ment |
Mean enroll-ment |
Elementary |
C-Small |
20,407 |
22.1% |
5,181,836 |
10.6% |
1 |
400 |
254 |
Elementary |
B-Medium |
17,054 |
18.5% |
8,427,056 |
17.3% |
401 |
600 |
494 |
Elementary |
A-Large |
12,148 |
13.2% |
9,307,740 |
19.1% |
601 |
3,017 |
766 |
Middle |
C-Small |
7,653 |
8.3% |
2,213,443 |
4.5% |
1 |
525 |
289 |
Middle |
B-Medium |
4,461 |
4.8% |
2,933,164 |
6.0% |
526 |
800 |
658 |
Middle |
A-Large |
3,891 |
4.2% |
4,056,410 |
8.3% |
801 |
2,719 |
1,043 |
High |
C-Small |
11,519 |
12.5% |
2,964,138 |
6.1% |
1 |
700 |
257 |
High |
B-Medium |
3,819 |
4.1% |
4,000,893 |
8.2% |
701 |
1,450 |
1,048 |
High |
A-Large |
3,176 |
3.4% |
6,582,044 |
13.5% |
1,451 |
5,323 |
2,072 |
Other |
|
8,021 |
8.7% |
3,048,441 |
6.3% |
1 |
10,840 |
380 |
Total |
|
92,149 |
100.0% |
48,715,165 |
100.0% |
|
|
|
The school design will define three major subgroups: non-Title I schools, Title I high-poverty schools, and Title I low/medium-poverty schools. Given the importance of Title I schools and the need to compare non-Title I schools to Title I schools, these subgroups are very important. Poverty status is defined for schools in terms of percentage of students eligible for free or reduced price lunch. The cutoff for high-poverty schools is the enrollment-weighted 75th percentile: 71.3 percent of students eligible for free or reduced lunch. Table B-5 presents the breakdown of school counts and enrollment according to the 2011-12 CCD frame.
Table B-5. Subgroups for the school sample design
Major school group |
Span |
School size group |
Frame count |
Percent of frame |
Total enrollment |
Percent of enroll-ment |
Mean enroll-ment |
Enroll-ment ratio |
3/4 root enroll-ment ratio |
Non-Title I |
Elem |
C-Small |
3,403 |
3.69% |
821,404 |
1.69% |
241 |
0.96 |
0.972 |
Non-Title I |
Elem |
B-Medium |
3,728 |
4.05% |
1,857,433 |
3.81% |
498 |
1.99 |
1.674 |
Non-Title I |
Elem |
A-Large |
3,093 |
3.36% |
2,383,100 |
4.89% |
770 |
3.07 |
2.321 |
Non-Title I |
Middle |
C-Small |
1,601 |
1.74% |
463,477 |
0.95% |
289 |
1.15 |
1.114 |
Non-Title I |
Middle |
B-Medium |
1,397 |
1.52% |
923,425 |
1.90% |
661 |
2.64 |
2.069 |
Non-Title I |
Middle |
A-Large |
1,410 |
1.53% |
1,483,074 |
3.04% |
1,052 |
4.20 |
2.931 |
Non-Title I |
High |
C-Small |
4,519 |
4.90% |
1,053,762 |
2.16% |
233 |
0.93 |
0.947 |
Non-Title I |
High |
B-Medium |
1,687 |
1.83% |
1,785,002 |
3.66% |
1,058 |
4.22 |
2.944 |
Non-Title I |
High |
A-Large |
1,366 |
1.48% |
2,735,095 |
5.61% |
2,002 |
7.99 |
4.751 |
Non-Title I |
Comb |
|
2,534 |
2.75% |
763,858 |
1.57% |
301 |
1.20 |
1.148 |
Non-Title I |
Total |
Total |
24,738 |
26.85% |
14,269,630 |
29.29% |
|
|
|
Title I high pov |
Elem |
C-Small |
5,765 |
6.26% |
1,542,521 |
3.17% |
268 |
1.07 |
1.050 |
Title I high pov |
Elem |
B-Medium |
5,019 |
5.45% |
2,480,152 |
5.09% |
494 |
1.97 |
1.663 |
Title I high pov |
Elem |
A-Large |
3,965 |
4.30% |
3,071,367 |
6.30% |
775 |
3.09 |
2.330 |
Title I high pov |
Middle |
C-Small |
1,776 |
1.93% |
528,941 |
1.09% |
298 |
1.19 |
1.138 |
Title I high pov |
Middle |
B-Medium |
862 |
0.94% |
563,944 |
1.16% |
654 |
2.61 |
2.053 |
Title I high pov |
Middle |
A-Large |
723 |
0.78% |
762,118 |
1.56% |
1,054 |
4.20 |
2.936 |
Title I high pov |
High |
C-Small |
1,778 |
1.93% |
482,116 |
0.99% |
271 |
1.08 |
1.061 |
Title I high pov |
High |
B-Medium |
432 |
0.47% |
429,155 |
0.88% |
993 |
3.96 |
2.808 |
Title I high pov |
High |
A-Large |
304 |
0.33% |
664,839 |
1.36% |
2,187 |
8.72 |
5.076 |
Title I high pov |
Comb |
|
1,845 |
2.00% |
642,171 |
1.32% |
348 |
1.39 |
1.279 |
Title I high pov |
Total |
Total |
22,469 |
24.38% |
11,167,324 |
22.92% |
|
|
|
Title I low pov |
Elem |
C-Small |
11,239 |
12.20% |
2,817,911 |
5.78% |
251 |
1.00 |
1.000 |
Title I low pov |
Elem |
B-Medium |
8,307 |
9.01% |
4,089,471 |
8.39% |
492 |
1.96 |
1.659 |
Title I low pov |
Elem |
A-Large |
5,090 |
5.52% |
3,853,273 |
7.91% |
757 |
3.02 |
2.291 |
Title I low pov |
Middle |
C-Small |
4,276 |
4.64% |
1,221,025 |
2.51% |
286 |
1.14 |
1.102 |
Title I low pov |
Middle |
B-Medium |
2,202 |
2.39% |
1,445,795 |
2.97% |
657 |
2.62 |
2.059 |
Title I low pov |
Middle |
A-Large |
1,758 |
1.91% |
1,811,218 |
3.72% |
1,030 |
4.11 |
2.886 |
Title I low pov |
High |
C-Small |
5,222 |
5.67% |
1,428,260 |
2.93% |
274 |
1.09 |
1.067 |
Title I low pov |
High |
B-Medium |
1,700 |
1.84% |
1,786,736 |
3.67% |
1,051 |
4.19 |
2.930 |
Title I low pov |
High |
A-Large |
1,506 |
1.63% |
3,182,110 |
6.53% |
2,113 |
8.43 |
4.946 |
Title I low pov |
Comb |
|
3,642 |
3.95% |
1,642,412 |
3.37% |
451 |
1.80 |
1.553 |
Title I low pov |
Total |
Total |
44,942 |
48.77% |
23,278,211 |
47.78% |
|
|
|
Total |
Total |
Total |
92,149 |
100.00% |
48,715,165 |
100.00% |
|
|
|
The enrollment ratio is the ratio of the mean enrollment for the subgroup as compared to the subgroup Title I low-poverty, small elementary schools. The ¾ root of this ratio is the basis for the sampling rate for the subgroups. This power is selected as it equalizes the precision for enrollment-based and count-based estimates (see the discussion below). The second part of this sampling rate is a multiplier for the three major subgroups. This multiplier is given in Table B-6 below.
Table B-6. Expected school sample sizes for the subgroups in the school sample design
Major school group |
Span |
School size group |
Percent of enroll-ment |
Percent of frame |
Relative sample rate |
Major school group multi- plier |
Final relative sample rate |
Expected sample size |
Percent of sample |
Non-Title I |
Elem |
C |
1.69% |
3.69% |
0.972 |
1.69 |
1.64 |
29.2 |
2.24% |
Non-Title I |
Elem |
B |
3.81% |
4.05% |
1.674 |
1.69 |
2.83 |
55.0 |
4.23% |
Non-Title I |
Elem |
A |
4.89% |
3.36% |
2.321 |
1.69 |
3.92 |
63.3 |
4.87% |
Non-Title I |
Middle |
C |
0.95% |
1.74% |
1.114 |
1.69 |
1.88 |
15.7 |
1.21% |
Non-Title I |
Middle |
B |
1.90% |
1.52% |
2.069 |
1.69 |
3.50 |
25.5 |
1.96% |
Non-Title I |
Middle |
A |
3.04% |
1.53% |
2.931 |
1.69 |
4.95 |
36.5 |
2.80% |
Non-Title I |
High |
C |
2.16% |
4.90% |
0.947 |
1.69 |
1.60 |
37.7 |
2.90% |
Non-Title I |
High |
B |
3.66% |
1.83% |
2.944 |
1.69 |
4.98 |
43.8 |
3.37% |
Non-Title I |
High |
A |
5.61% |
1.48% |
4.751 |
1.69 |
8.03 |
57.2 |
4.40% |
Non-Title I |
Comb |
|
1.57% |
2.75% |
1.148 |
1.69 |
1.94 |
25.7 |
1.97% |
Non-Title I |
|
|
29.29% |
26.85% |
0.000 |
|
|
389.6 |
29.97% |
Title I high pov |
Elem |
C |
3.17% |
6.26% |
1.050 |
2.73 |
2.87 |
86.2 |
6.63% |
Title I high pov |
Elem |
B |
5.09% |
5.45% |
1.663 |
2.73 |
4.54 |
118.9 |
9.15% |
Title I high pov |
Elem |
A |
6.30% |
4.30% |
2.330 |
2.73 |
6.36 |
131.6 |
10.13% |
Title I high pov |
Middle |
C |
1.09% |
1.93% |
1.138 |
2.73 |
3.11 |
28.8 |
2.21% |
Title I high pov |
Middle |
B |
1.16% |
0.94% |
2.053 |
2.73 |
5.60 |
25.2 |
1.94% |
Title I high pov |
Middle |
A |
1.56% |
0.78% |
2.936 |
2.73 |
8.02 |
30.2 |
2.33% |
Title I high pov |
High |
C |
0.99% |
1.93% |
1.061 |
2.73 |
2.90 |
26.9 |
2.07% |
Title I high pov |
High |
B |
0.88% |
0.47% |
2.808 |
2.73 |
7.67 |
17.3 |
1.33% |
Title I high pov |
High |
A |
1.36% |
0.33% |
5.076 |
2.73 |
13.86 |
22.0 |
1.69% |
Title I high pov |
Comb |
|
1.32% |
2.00% |
1.279 |
2.73 |
3.49 |
33.6 |
2.59% |
Title I high pov |
|
|
22.92% |
24.38% |
0.000 |
|
|
520.8 |
40.06% |
Title I low pov |
Elem |
C |
5.78% |
12.20% |
1.000 |
1.00 |
1.00 |
58.7 |
4.51% |
Title I low pov |
Elem |
B |
8.39% |
9.01% |
1.659 |
1.00 |
1.66 |
71.9 |
5.53% |
Title I low pov |
Elem |
A |
7.91% |
5.52% |
2.291 |
1.00 |
2.29 |
60.8 |
4.68% |
Title I low pov |
Middle |
C |
2.51% |
4.64% |
1.102 |
1.00 |
1.10 |
24.6 |
1.89% |
Title I low pov |
Middle |
B |
2.97% |
2.39% |
2.059 |
1.00 |
2.06 |
23.7 |
1.82% |
Title I low pov |
Middle |
A |
3.72% |
1.91% |
2.886 |
1.00 |
2.89 |
26.5 |
2.04% |
Title I low pov |
High |
C |
2.93% |
5.67% |
1.067 |
1.00 |
1.07 |
29.1 |
2.24% |
Title I low pov |
High |
B |
3.67% |
1.84% |
2.930 |
1.00 |
2.93 |
26.0 |
2.00% |
Title I low pov |
High |
A |
6.53% |
1.63% |
4.946 |
1.00 |
4.95 |
38.9 |
2.99% |
Title I low pov |
Comb |
|
3.37% |
3.95% |
1.553 |
1.00 |
1.55 |
29.5 |
2.27% |
Title I low pov |
|
|
47.78% |
48.77% |
|
|
|
389.6 |
29.97% |
Total |
|
|
100.00% |
100.00% |
|
|
|
1300.0 |
100.00% |
The major subgroup multipliers were generated with the goal of making the non-Title I, Title I low/medium -poverty, and Title I high-poverty schools 30 percent, 30 percent, and 40 percent of the overall school sample respectively and thus, close to equal in size. To do this, the Title I high-poverty schools need to be sampled at a 2.73 higher rate than the Title I low-poverty schools, and the non-Title I schools at a 1.69 times higher rate than the Title I low-poverty schools. Table B-7 presents the effective sample sizes for all schools and for the three major subgroups, and for enrollment-based and count-based school estimates. As can be seen the precision for the two types of estimates is close: that is the ‘minimax’ property. The effective sample sizes across the three subgroups are roughly the 30-30-40 breakdown which was desired.
Table B-7. Power properties of school design
Power Property |
Sample size |
Enrollment-based weight estimates |
Count-based weight estimates |
Effective sample size: All schools |
1,300 |
937 |
918 |
Effective sample size: Non-Title I schools |
389 |
319 |
309 |
Effective sample size: Title I low/medium-poverty schools |
390 |
334 |
328 |
Effective sample size: Title I high-poverty schools |
521 |
460 |
456 |
The
school sample is nested within the district sample, so this
constitutes a clustered design. This will facilitate school
recruiting and will allow for a comparison of school and district
responses within the sampled districts. The final school
probabilities are equal to the unconditional probabilities developed
based on the school design described in Table B-6, divided by the
district probabilities of selection. This clustered design means that
intra-district correlation among the schools in each district will
affect the precision of the estimates. Table B-8 presents the
effective sample sizes under a variety of different intra-district
correlation coefficients. The mean number of sampled schools per
sampled district is 2.28 (1,300 schools divided by 570 districts). We
will approximate the design effect due to district clustering as
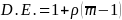 ,
with
,
with
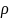 the intra-district correlation coefficient, and
the intra-district correlation coefficient, and
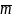 the mean cluster size 2.28.
the mean cluster size 2.28.
Table B-8. Effective sample sizes for national school-level estimates under the 3/4th root school design
Intra-district correlation coefficient |
Within-district mean school sample size |
Design effect |
Effective enrollment-based weight school sample size |
Effective count-based weight school sample size |
CV of enrollment-based weight estimate |
CV of count-based weight estimate |
|
|
|
|
|
|
|
0% |
2.28 |
1.000 |
936.9 |
917.9 |
3.27% |
3.30% |
5% |
2.28 |
1.064 |
880.5 |
862.7 |
3.37% |
3.40% |
10% |
2.28 |
1.128 |
830.6 |
813.7 |
3.47% |
3.51% |
15% |
2.28 |
1.192 |
786.0 |
770.0 |
3.57% |
3.60% |
20% |
2.28 |
1.256 |
745.9 |
730.8 |
3.66% |
3.70% |
25% |
2.28 |
1.320 |
709.8 |
695.4 |
3.75% |
3.79% |
30% |
2.28 |
1.384 |
676.9 |
663.2 |
3.84% |
3.88% |
35% |
2.28 |
1.448 |
647.0 |
633.9 |
3.93% |
3.97% |
40% |
2.28 |
1.512 |
619.6 |
607.1 |
4.02% |
4.06% |
45% |
2.28 |
1.576 |
594.5 |
582.4 |
4.10% |
4.14% |
50% |
2.28 |
1.640 |
571.3 |
559.7 |
4.18% |
4.23% |
The effective sample sizes comparing non-Title I, Title I high-poverty, and Title I low-poverty schools are given in Table B-7, depending on the type of estimate (enrollment-based or count-based). The lowest precision is for the pair non-Title I schools vs. Title I low/medium-poverty schools with count-based estimates, where the effective sample sizes are 309 and 328 respectively. Assuming no effect from intra-district correlation, this translates to an MDES of 22.2 percent for comparing non-Title I and Title I high- poverty schools, and slightly lower MDES for the other possible pairs.18
Further Details of School Sampling. The school sample is nested within the district sample, and districts will then be the major stratum for school sampling. The mean school sample size per district is very small (2.28), so there is not much room for stratification at the school level beyond districts, but we will implicitly stratify by Title I status (i.e., within districts, systematically sample the schools sorted by Title I status), and if there is sufficient sample size, by school span (elementary, middle/combined, high).19
B.2.2.3. Nationally representative sample of teachers of core academic subjects and special education
The teacher sample will be 9,100 teachers of core academic subjects and special education, sampled in 1,300 sampled schools: a mean of 7.0 teachers per sampled school. Expecting at least 85 percent teacher response, this will result in 7,735 expected completed surveys, a mean value of 5.95 teachers per sampled school.
The teacher sample sizes per school will vary across schools. The plan is to set the teacher sample size in a way to equalize the final teacher weights within the four basic school-span strata (elementary, middle, high, and combined schools), to the extent possible, given the need to have integer teacher sample sizes. Our plan will be similar to that used for teacher sampling in SASS (Schools and Staffing Survey), carried out by the NCES. Documentation regarding SASS teacher sampling can be found in http://www.nces.ed.gov/surveys/sass. SASS is done once every four years (2003/2004, 2007/2008, 2011/2012).
We
define a school weight
 for stratum
for stratum
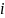 (
(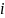 =1,…,
=1,…,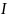 )
and school
)
and school
 (
( =1,…,
=1,…, ).
This is the inverse of the school probability of selection,
disregarding oversampling for the three major school subgroups (we
adjust for differential probabilities due to enrollment, but not due
to school Title I status and school poverty status).20
Define
).
This is the inverse of the school probability of selection,
disregarding oversampling for the three major school subgroups (we
adjust for differential probabilities due to enrollment, but not due
to school Title I status and school poverty status).20
Define
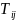 as the teacher count for school
as the teacher count for school
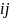 .
Define
.
Define
 as
the mean per-school eligible teacher sample size for stratum
as
the mean per-school eligible teacher sample size for stratum
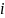 ,
and
,
and
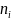 as the school sample size in stratum
as the school sample size in stratum
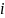 .
The teacher sample size for school
.
The teacher sample size for school
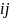 will be
will be

where
INT is the function that rounds to the nearest positive integer. Note
that if the school probability of selection was directly proportional
to eligible teacher count, then
 and
and
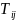 would be equal to a constant within each stratum
would be equal to a constant within each stratum
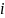 and
the teacher sample size would be simply
and
the teacher sample size would be simply
 for each schoolin stratum
for each schoolin stratum
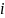 .
The schools are sampled very roughly proportionally to the ¾-root
of enrollment within the two major strata (high-poverty districts and
low/medium-poverty districts), so assuming that teacher count is
proportional to enrollment (roughly) in the school strata,
.
The schools are sampled very roughly proportionally to the ¾-root
of enrollment within the two major strata (high-poverty districts and
low/medium-poverty districts), so assuming that teacher count is
proportional to enrollment (roughly) in the school strata,
 will tend to be inversely proportional to the ¾-root of
will tend to be inversely proportional to the ¾-root of
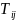 ,
making teacher sample size roughly proportional to the ¼ root
of teacher count. Thus, the teacher count will be slightly larger for
larger schools, and slightly smaller for smaller schools, but not far
from
,
making teacher sample size roughly proportional to the ¼ root
of teacher count. Thus, the teacher count will be slightly larger for
larger schools, and slightly smaller for smaller schools, but not far
from
 unless the teacher-student ratio is unusual for the school, or the
school’s enrollment is on the extreme end of the distribution
for the school stratum. An upper bound of 10 is placed on the teacher
sample size per school to minimize burden.
unless the teacher-student ratio is unusual for the school, or the
school’s enrollment is on the extreme end of the distribution
for the school stratum. An upper bound of 10 is placed on the teacher
sample size per school to minimize burden.
Within the three major school subgroups, the design for teachers should be close to self-weighting. We will assume design effects of 1.15 to allow for distortions from rounding to integers, respecting the maximum burden of 10, and to also allow for the effect of necessary teacher nonresponse adjustments. Table B-9 below summarizes the design and calculates effective teacher sample sizes assuming the design effect of 1.15 within the three major school subgroups, and the design effect from oversampling the high-poverty Title I and non-Title I schools by factors of 2.73 and 1.69 respectively (relative to low-poverty Title I schools). The calculations of effective sample sizes in Table B-9 do not yet include any design effects from intra-school correlation between teachers. The effects of this in reducing effective teacher sample sizes from the numbers given in the rightmost column in Table B-9 are provided in Table B-10.
Table B-9. Expected teacher sample sizes
School subgroup |
Expected school sample size |
Mean sampled teachers per school |
Total sampled teachers |
Percent of sample teachers |
Percent of pop'n teachers |
Expected teacher response rate |
Expected final teachers per school |
Total final teacher count |
Effective teacher sample size |
Non-Title I |
389 |
7 |
2,723 |
29.90% |
29.29% |
85% |
5.95 |
2,315 |
2,013 |
Title I low pov |
390 |
7 |
2,730 |
30.00% |
47.78% |
85% |
5.95 |
2,321 |
2,018 |
Title I high pov |
521 |
7 |
3,647 |
40.10% |
22.92% |
85% |
5.95 |
3,100 |
2,696 |
Total |
1,300 |
7 |
9,100 |
100.00% |
100.00% |
85% |
5.95 |
7,735 |
5,706
|
Table
B-10 presents the final effective sample sizes for national teacher
estimates under a variety of different intra-school correlation
coefficients. The mean number of final teachers per sampled school is
5.95. We will approximate the design effect due to school clustering
as
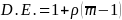 ,
with
,
with
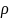 the intra-school correlation coefficient, and
the intra-school correlation coefficient, and
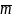 the mean cluster size 5.95.
the mean cluster size 5.95.
Table B-10. Effective sample sizes for national teacher estimates
Intra-school correlation coefficient |
Within-school mean teacher sample size |
Design effect |
Final effective teacher sample size |
0% |
5.95 |
1.000 |
5,706 |
5% |
5.95 |
1.248 |
4,574 |
10% |
5.95 |
1.495 |
3,816 |
15% |
5.95 |
1.743 |
3,274 |
20% |
5.95 |
1.990 |
2,867 |
25% |
5.95 |
2.238 |
2,550 |
30% |
5.95 |
2.485 |
2,296 |
35% |
5.95 |
2.733 |
2,088 |
40% |
5.95 |
2.980 |
1,915 |
45% |
5.95 |
3.228 |
1,768 |
50% |
5.95 |
3.475 |
1,642 |
We are also interested in generating estimates for teachers of core academic subjects and special education separately for elementary, middle, and high schools. Table B-11 provides expected sample sizes for each of these three span subgroups. The expected final eligible teachers per school are our expectations for the average number of teacher surveys given the expected school sample sizes and an assumed allocation of teachers by school span based on enrollment percentages21 (6.2, 7.3, and 8.8 sampled teachers for elementary, middle, and high schools respectively, with an 85 percent response rate to obtain the expected surveyed teacher means of 5.27, 6.21, and 7.48 respectively). The effective sample size for the major subgroups assumes a design effect of 1.15 (accounting for teacher nonresponse adjustments and varying teacher sample sizes). The effective sample size for the three subgroups combined within grade span also includes the design effect induced from oversampling non-Title I schools and high-poverty Title I schools, by benchmarking by subgroup enrollment figures (assuming that student enrollment is exactly proportional to teacher counts). Note that these are not ‘final’ effective sample sizes that also include a design effect from intra-school correlations.
Table B-11. Sample sizes and effective sample sizes for teachers of core academic subjects and special education for elementary, middle, and high schools
Span |
Major school group |
Expected school sample size |
Expected final teachers per school |
Total final teachers |
Effective sample size |
Enrollment |
Elementary |
Non-Title I |
148 |
5.27 |
777 |
676 |
5,061,937 |
Elementary |
Title I low pov |
191 |
5.27 |
1,009 |
877 |
10,760,655 |
Elementary |
Title I high pov |
337 |
5.27 |
1,775 |
1,543 |
7,094,040 |
Elementary |
Total |
676 |
|
3,561 |
2,593 |
22,916,632 |
Middle |
Non-Title I |
78 |
6.205 |
482 |
419 |
2,869,976 |
Middle |
Title I low pov |
75 |
6.205 |
464 |
403 |
4,478,038 |
Middle |
Title I high pov |
84 |
6.205 |
523 |
455 |
1,855,003 |
Middle |
Total |
237 |
|
1,468 |
1,101 |
9,203,017 |
High |
Non-Title I |
139 |
7.48 |
1,038 |
903 |
5,573,859 |
High |
Title I low pov |
94 |
7.48 |
703 |
611 |
6,397,106 |
High |
Title I high pov |
66 |
7.48 |
495 |
430 |
1,576,110 |
High |
Total |
299 |
|
2,235 |
1,713 |
13,547,075 |
Total |
Total |
1,211 |
5.99 |
7,265 |
5,406 |
45,666,724 |
Note: combined schools are not included in this table.
Table
B-12 presents power calculations for each grade span grouping, with
the effective teacher sample sizes as given in Table B-11. The first
effective sample size accounts for school sampling and teacher
weighting effects. The ‘final effective sample size’ also
accounts for intra-school correlation, using the design effect
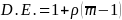 with
with
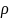 equal to the intra-school correlation and
equal to the intra-school correlation and
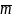 equal to the cluster size (the average number of surveyed teachers
per school). The assumed intra-school correlations for this table are
40 percent for elementary schools, 30 percent for middle schools, and
20 percent for high schools (we assume higher clustering due to the
small size and assumed ‘homogeneity’ within elementary
schools).
equal to the cluster size (the average number of surveyed teachers
per school). The assumed intra-school correlations for this table are
40 percent for elementary schools, 30 percent for middle schools, and
20 percent for high schools (we assume higher clustering due to the
small size and assumed ‘homogeneity’ within elementary
schools).
Table B-12. Sample sizes and effective sample sizes for teachers of core academic subjects and special education for elementary, middle, and high school grade spans
Span |
Expected final teachers |
Effective sample size (0% ICC) |
Assumed intra-school correlation |
Cluster size |
Design effect |
Final effective sample size |
Elementary |
3,561 |
2,593 |
40% |
5.27 |
2.708 |
958 |
Middle |
1,468 |
1,101 |
30% |
6.205 |
2.5615 |
430 |
High |
2,235 |
1,713 |
20% |
7.48 |
2.296 |
746 |
Note: combined schools are not included in this table.
Within each school, eligible teachers will be selected in an equal probability sample. Eligible teachers are those whose subject most often taught is reading/English/language arts, mathematics, science, social studies, general elementary, or special education. The overall teacher sample size will be determined by the SASS-type algorithm given above. There will be an expected value of seven sampled teachers per school, with a maximum of 10 sampled teachers in any one school.
The sample will be implicitly stratified. A sort order will be defined, and a systematic sample taken. This controls to a certain extent the sample sizes across the subgroups, especially for the first sort variable. The first sort variable in this case is whether the teacher is an ESEA-tested teacher. That is, a teacher who teaches any class whose students are tested for ESEA accountability requirements. Thus, the sample breakdown for ESEA/non-ESEA tested teachers will be close to the sampled school’s percentages among eligible teachers within the school. Doing this consistently over all the sampled schools should bring the sample percentages for ESEA/non-ESEA teachers close to national percentages.
Within the ESEA/non-ESEA status, the sort order will be by grade level, and then by subject and/or special education status, in a ‘serpentine’ manner22. This will provide some very limited balance across grade levels, subject, and special education status within ESEA/non-ESEA status.
In
general, intra-school correlation between teachers reduces the
efficiency of teacher estimates, as can be seen in Table B-12. But
comparing subgroups which are both present in every school (or in
most schools, at least) will benefit
from the presence of positive intra-school correlation. The estimate
in this case is in effect a comparison of the two subgroups within
each school, aggregated over all schools. The variance in this case
will be proportional to
 ,
where
,
where
 is the effective school sample size (accounting for design effects
from oversampling of the three major school subgroups, but not
accounting for design effects from enrollment-based oversampling, as
the latter is removed in the setting of teacher sample sizes),
is the effective school sample size (accounting for design effects
from oversampling of the three major school subgroups, but not
accounting for design effects from enrollment-based oversampling, as
the latter is removed in the setting of teacher sample sizes),
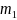 and
and
 are the sample sizes for the subgroups, and
are the sample sizes for the subgroups, and
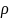 is the intra-school correlation for the characteristic. Note that the
variance decreases linearly with
is the intra-school correlation for the characteristic. Note that the
variance decreases linearly with
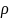 .
.
Table B-13 provides MDES calculations for a comparison of ESEA and non-ESEA teachers within elementary schools, middle schools, and high schools, assuming intra-school correlations of 40%, 30%, and 20% respectively.23 The proportion of ESEA teachers will vary across schools, depending on the grade structure. The calculations below are for an expected responding teacher sample size divided into two subgroups of size 75% and 25%.24 This calculation will be conservative (an upper bound on the variance) for any ESEA percentages between 25% and 75%. In all cases, the null hypothesis is no difference, with a two-sided test with alpha-level 5 percent, and 80 percent power for the alternative. The MDES are very good in all cases.
Table B-13. Selected MDES for teachers by elementary, middle, and high school grade spans
Span |
Effective school sample size |
Assumed intra-school correlation |
Final expected survey sample size |
Final survey sample size subgroup 1 |
Final survey sample size subgroup 2 |
MDES |
Elementary |
566 |
40% |
5.27 |
3.95 |
1.32 |
9.17% |
Middle |
204 |
30% |
6.20 |
4.65 |
1.55 |
15.21% |
High |
263 |
20% |
7.48 |
5.61 |
1.87 |
13.03% |
B.2.3. Estimation Procedures
The focus of the report will be on the progress being made on the core policies promoted by Titles I and II. While simple descriptive statistics such as means and percentages will provide answers to many of our questions, cross-tabulations will be important to answering questions about variation across state, district, schools, and teacher characteristics.
Whether a state received an approved ESEA Flexibility request from the U.S. Department of Education. This is of interest because ESEA Flexibility is expected to influence the design of state accountability systems and approaches to educator quality measurement and policy makers will be interested in what states do with the ESEA Flexibility.
District poverty level, size, urbanicity, and concentration of English learners. Poverty is included because Title I is specifically intended to ameliorate the effects of poverty on local funding constraints and educational opportunity. Urbanicity is included because of the relationships between educational opportunity and rural isolation and the concentration of poverty in urban schools. Size is included because it may be related to district capacity to develop and implement programs. Concentration of English learners is included because of the increased emphasis on ensuring that this group of students also meets state content standards and recognition that modifications in testing as well as instruction will be needed to facilitate progress of these students.
School Title I status, grade span (high school, middle, and elementary grades), poverty level, and cross classifications of Title I status and poverty level. Grade span is included because the implementation of state content standards and aligned assessments as well as responses to accountability systems likely differs by grade level. Title I status is included because the focus of Title I funds and requirements is to influence state and district policy and school effectiveness. We plan to cross-classify Title I status with school poverty because there may be substantial differences between what happens in high-poverty Title I schools in comparison with Title I schools with low/medium-poverty levels, which may be more similar to schools which do not receive Title I funding.
Teacher grade span taught and whether the teacher teaches a grade or subject in which state testing is required by ESEA. These characteristics are included because teachers’ responses to state content standards, assessments, accountability systems, and teacher evaluations based on student growth may vary by grade span, and by whether they teach tested subjects or grades.
The use of stratification (and oversampling when necessary) in our sample design was introduced to ensure reasonable power for specific subgroup comparisons, and our samples are expected to include units that vary on other characteristics (e.g., urbanicity) to allow the comparisons described above.
Because of the use of a statistical sample, survey data presented for districts, schools, and teachers will be weighted to national totals (tabulations will, provide standard errors for the reported estimated statistics). In addition, the descriptive tables will indicate where differences between subgroups are statistically significant. We will use Chi-Square tests to test for significant differences among distributions and t-tests for differences in means. Tabulations will be included in the reports where appropriate.
Please see Section B.3.1 for a discussion of our weighting procedures.
B.2.4. Degree of Accuracy Needed
We require statistical precision at all three levels in this study: the district level, the school level, and the teacher level. This makes this study different from a study which is focused for example on teachers alone. The hardest level to achieve precision for will be the district level, as the sample sizes in the three-stage sample design have to be smallest at this level (being the first stage of selection). The sample size of 570 districts roughly evenly split between high-poverty districts and the complement stratum will provide an MDES of 30% for comparing these two important district subgroups.
At the school level, we are sampling 1,300 schools. An important analysis at the school level compares Title I high-poverty schools (roughly 25% of the population), Title I low/medium-poverty schools (roughly 45% of the population), and non-Title I schools (roughly 30% of the population). We oversample Title I high-poverty schools considerably (a factor of 2.73), and non-Title I schools slightly (a factor of 1.69), to achieve a 30%-40%-30% split respectively in the sample sizes. The MDES for the three possible pair-wise comparisons ranges between 22% and 25%, depending on the degree of intra-school correlation.
At the teacher level, we are sampling 9,100 teachers of core academic subjects and special education, and expecting 7,735 respondents. This sample size will be sufficient to provide MDESs below 20% for comparisons between ESEA and non-ESEA teachers among elementary schools, middle schools, and high schools separately. The MDESs depend on the intra-school correlation and how the ESEA percentages break across the schools (each subgroup represented in each school, or each subgroup is more concentrated in particular schools). The highest precision is achieved when the ESEA percentage is close to 50%, and is lower when the ESEA percentage is significantly smaller or larger than 50%.
B.2.5. Unusual Problems Requiring Specialized Sampling Procedures
There are no unusual problems requiring specialized sampling procedures.
B.2.6. Use of Periodic (less than annual) Data Collection to Reduce Burden
This data will be collected during the 2013-14 school year with a follow up survey and a possible optional year. This OMB package addresses only the 2013-14 school year data collection.
B.3. Methods to Maximize Response Rates
We plan to work
with states, school districts, schools, and teachers to explain the
importance of this data collection effort and to make it as easy as
possible to comply. For all respondents, a clear description of the
study design, the nature and importance of the study, and the OMB
clearance information will be provided.
For the states, the data collection’s reliance whenever possible on administrative and extant data, thereby limiting the data collection from state representatives, will encourage cooperation with evaluation efforts. We will be courteous but persistent in follow-up with participants who do not respond in a timely manner to our attempts. As noted earlier, we will also be very flexible gathering our data, allowing different people to respond to the different content areas and in whichever mode is easiest -- electronic, hard copy or telephone format.
For the school districts, schools, and teachers, we will initiate several forms of follow-up contacts with respondents who have not responded to our communication. We will use a combination of reminder postcards, emails and follow-up letters to encourage respondents to complete the surveys. The project management system developed for this study will be the primary tool for monitoring whether surveys have been initiated. After 10 days, we will send an email message (or postcard for those without email) to all non-respondents indicating that we have not received a completed survey and encouraging them to submit one soon. Within seven business days of this first follow-up, we will mail non-respondents a hard copy package including all materials in the initial mailing. Ten days after the second follow-up, we will telephone the remaining non-respondents to ask that they complete the survey and offer them the option to answer the survey by phone, either at that time or at a time to be scheduled during the call.
To maximize response rates, we also will (1) provide clear instructions and user-friendly materials, (2) offer technical assistance for survey respondents using a toll-free telephone number or email, (3) monitor progress regularly, and (4) provide incentives for principals ($25) and teachers ($20). In recognition of the fact that district and school administrators have many demands on their time, and typically, these administrators receive numerous requests to participate in studies and complete surveys for federal and state governments, district offices, and independent researchers, we plan to identify a district liaison. For most districts, completion of the district survey will require input from multiple respondents, and the district liaison’s role will be pivotal in positively impacting participation, collecting high quality data, and achieving an 85 percent response rate.
B.3.1. Weighting the district, school, and teacher samples
After completion of the field data collection in each year, we plan to weight the data to provide a nationally representative estimator at the district, school, and teacher level. Replicate weights will be generated to provide consistent jackknife replicate variance estimators (statistical packages such as STATA and SAS Version 9.2 allow for easy computation of replicate variance estimates). The development of replicate weights will facilitate the computation of standard errors for the complex analyses necessary for this survey. The replicates will be based fundamentally on the district sample (the first stage of selection), with an exception for certainty districts, for which the first stage of selection is at the school level. We anticipate limited nonresponse at the district and school level, which we will adjust for by utilizing information about the non-responding districts and schools from the frame. This information will be used to generate nonresponse cells with differential response propensities. The nonresponse adjustments will be equal to the ratio of the frame weighted count to the sum of weights for respondents. This will adjust for bias from nonresponse, and also adjust for differences from the frame (accomplishing poststratification). If the cell structure is too rich, we may utilize raking (multi-dimensional adjustment). The cell structure for districts will include district poverty status, Census region, urbanicity, and district size. The cell structure for schools will include district poverty status, school poverty status, Title I status, Census region, urbanicity, and school size.
There are two types of district and school weights that will be generated: enrollment-based weights and count-based weights. The first set of weights will add to total enrollment and the second to the simple count of districts and schools on the frame. A separate set of nonresponse adjustments will be calculated for each set of weights. Trimming may be utilized if necessary to scale back extreme weights.
We expect a larger degree of teacher nonresponse (though we plan to provide an incentive). Teacher nonresponse adjustments will be computed based on an analysis of district and school characteristics, and teacher characteristics known from the teacher rosters, which correlate to teacher propensity to respond. A ‘frame of teachers of core academic subjects and special education’ will be created by weighting the teacher rosters from the sampled schools using the final teacher weights. The starting point for teacher weights will be the enrollment-based final school weights. Teacher adjustments will then be made equaling the teacher roster totals divided by the weighted totals over teacher respondents. Raking may be utilized if the cell structure is too rich. The cell structure will include district poverty status, school poverty status, Title I status, Census region, and school size. Trimming may be utilized if necessary to scale back extreme weights, if this occurs.
B.4. Test of Procedures
The state survey
will be pretested with up to three states, and prior to the pretest,
we will gather documentation and extant data from their state
websites to better understand how current is the information obtained
from secondary sources. The school district, school, and teacher
surveys will be pretested with nine or fewer respondents. We will
also pretest the teacher roster with principals to determine that the
requested data is sufficient for selecting the teachers.
B.5. Individuals Consulted on Statistical Aspects of Design
The
individuals consulted on the statistical aspects of the design
include:
Camilla Heid, Westat, Project Director, 301-294-4413
Patty Troppe, Westat, Deputy Project Director, 301-294-3924
Anthony Milanowski, Westat, Co-Principal Investigator, 240-453-2718
Brian Gill, Mathematica, Co-Principal Investigator, 617-301-8962
Lou Rizzo, Westat, Senior Statistician, 301-294-4486
David Morganstein, Westat, Vice-President Statistical Group, 301-251-8215
Tom Cook, Northwestern University, 847-491-3776
Sean Reardon, Stanford University, Member of Technical Working Group, 650-736-8517
Gottfredson, G. D., Gottfredson, D. C., Payne, A., & Gottfredson, N. C. (2005). School climate predictors of school disorder: Results from a National Study of Delinquency Prevention in Schools. Journal of Research In Crime And Delinquency, 42(4), 412-444.
Ingersoll, R. M., & May, H. (2012). The magnitude, destinations, and determinants of mathematics and science teacher turnover. Educational Evaluation and Policy Analysis, 34(4), 435-464.
Kelley, C., Heneman, H. & Milanowski, A., (1999). School-Based Performance Awards: Research Findings and Future Directions. Madison, WI: Consortium for Policy Research in Education & Wisconsin Center for Education Research.
Nelsestuen, K., Scott, C., Hanita, M., Robinson, L., & Coskie, T. (2009). New and experienced teachers in a school reform initiative: The example of reading first. Issues & answers. REL 2009-082. Portland, OR: Regional Educational Laboratory at Education Northwest.
U.S. Department of Education. (2011, September 23). ESEA Flexibility. Retrieved from: http://www.ed.gov/esea/flexibility.
U.S. Department of Education. (2012a). Improving Basic Programs Operated by Local Educational Agencies (Title I, Part A). Retrieved from: http://www2.ed.gov/programs/titleiparta/index.html
U.S. Department of Education. (2012b). Findings from the 2011-2012 Survey on the Use of Funds Under Title II, Part A. Retrieved from: http://www2.ed.gov/programs/teacherqual/resources.html
1 Teachers who teach core academic subjects and special education are K through 12th grade teachers whose subject most often taught is reading/English/language arts, mathematics, science, social studies, general elementary, or special education.
2 The minimax design differs from the one used for the last Title I study. The previous study selected districts probability proportional to size (PPS), with size measured by student enrollment. The PPS design is quite efficient for estimating the proportion of students enrolled in districts implementing policies of interest. However, when estimating the percent of districts implementing a policy, the PPS design is relatively inefficient, compared to a simple random sample. This is because relatively few small and medium-sized districts are included in a PPS design. This, in turn, requires the small and medium-sized districts in the sample to be given greater weight to better represent the population of districts nationwide and can lead to relatively wide confidence intervals around estimates of proportions of districts.
3 Since the majority of non-Title I schools are low/medium-poverty schools, these schools will not be broken out by poverty status.
4 The cutoff for high-poverty schools is the enrollment-weighted 75th percentile: this is 71.3 percent of students eligible for free or reduced lunch on an earlier frame.
5 Under ESEA, as reauthorized by the No Child Left behind Act (NCLB) of 2001, public school students are tested annually in reading/English language arts and mathematics in grades 3 through 8, and once in high school. Students are tested in science once in each of the following grade groupings: grades 3-5, grades 6-9, and grades 10-12.
6 For this study we consider ESEA tested teachers as those core academic and special education teachers who teach any class whose students are tested for ESEA accountability requirements.
7 Schools will be asked to identify Kindergarten through 12th grade teachers in the school whose subject most often taught is reading/English/language arts, mathematics, science, social studies, general elementary, or special education.
8 If requested, the study team will contact each relevant state-level staff member directly to complete the survey.
9 This percentile is weighted by enrollment, and is found using the U.S. Bureau of the Census school district SAIPE (Small Area Income and Poverty Estimates). Linking the most recent SAIPE District data file to the 2011-12 Common Core of Data District Universe Frame, we found that this 75th percentile is 27.7% percent of families in poverty.
10 1.8 is the 0.535 root of 3.
11 This design is close to a ‘square root’ design, except that it is stratified design rather than a fully PPS design (sampling rates are equal within strata), and the root used is slightly larger than ½.
12 As processed to drop ineligible schools and entities, schools with no enrollment, etc.
13 The effective sample size is equal to the population variance divided by the sampling variance under the design.
14 We assume a null hypothesis of no difference with a two-sided critical region with a 5 percent alpha level. We find the smallest population difference that would be detectable with this test with 80 percent power. The MDES is this population difference divided by the (assumed) common population standard deviation for each subgroup.
15 This assumes 100 percent district response. District nonresponse will degrade these power results, but we expect minimal district nonresponse as this study is by law mandatory for the districts.
16 In defining district eligibility, we follow the criteria from the NAEP. The NAEP macros for excluding districts are applied also in the generation of the district frame here.
17 For sampling purposes, we will use the Title I status variable that is on the CCD that indicates whether the school is a Title I eligible school. We will confirm whether a sampled school received Title I for the 2013-2014 school year or remained Title I eligible.
18 Note that the effect of a positive intra-district correlation could be to either increase or decrease the precision, as we expect many low/medium-poverty districts to have at least one non-Title I school and one Title I school. For these districts, the presence of intra-district correlation actually increases the precision of the difference between the two subgroups. For other districts which have more than one of one subgroup, but none of the other, positive intra-district correlation will reduce the precision of the difference. Thus the overall effect will be ambiguous (depends on the exact distribution of the sampled schools across the sampled districts).
19 We would implicitly stratify by school span for example if all schools in a district were Title I, or non-Title I, or if the district sample size happened to be larger.
20 This means that teacher sample sizes will be larger for schools which were undersampled due to enrollment, and smaller for schools which were oversampled due to enrollment, bringing teacher sample sizes back to population percentages. However, for the three major subgroups, this reversion to population percentages will not take place. All other things being equal, teacher sample sizes within each school across the three major subgroups will not be different, resulting in an oversample of teachers in high-poverty Title I schools, roughly proportional to the 2.73 oversampling rate for these schools, and a slight oversample in non-Title I schools (a 1.69 oversampling rate), as compared to low/medium-poverty Title I schools.
21 Teacher allocations by grade span based on enrollment percentages are only provisional (it cannot be expected that eligible teacher/student ratios are exactly equal across grade spans). Final allocations of teacher sample sizes by grade span will only be produced after the school sample is fielded and teacher listings collected.
22 i.e., within the two primary subgroups ESEA/non-ESEA status, the sort order for grade level will be lowest grade to highest grade for ESEA teachers, and highest grade to lowest grade for non-ESEA teachers . With the systematic sampling procedure (every kth teacher), this will minimize the instances of 2 two teachers at the same grade being selected across neighboring cells. The sort order for subjects will be for example special ed to social science with ESEA-grade m, social science to special ed within ESEA-grade m+1, etc.
23 See Nelsestuen, K., Scott, C., Hanita, M., Robinson, L., & Coskie, T. (2009); Ingersoll, R. M., & May, H. (2012); Kelley, C., Heneman, H .& Milanowski, A., (1999); and Gottfredson, G. D., Gottfredson, D. C., Payne, A., & Gottfredson, N. C. (2005).
24 The effective school sample sizes are for enrollment-based estimates accounting for design effects from the minimax design (see Table B-11). Expected final teachers come from Table B-11. An added design effect of 1.15 is added for differential teacher weights.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Modified | 0000-00-00 |
| File Created | 2021-01-28 |
© 2026 OMB.report | Privacy Policy