SE Appendix L - B2 Details
SE 4 1 34 OMB Clearance Appendix L_ 4 18 14.docx
The Impact of Professional Development in Fractions for Fourth Grade
SE Appendix L - B2 Details
OMB: 1850-0909
Appendix L - Details for Question B2
Power estimates
To control for costs, the study team powered the study to detect student outcomes only. The student outcome for confirmatory analysis in this study is fractions achievement measured by the Test of Understanding of Fractions (TUF). Teacher-level outcomes such as impacts on teacher knowledge are considered to be useful as exploratory analyses. Our preliminary power estimates1 for the student outcomes indicate that approximately 80 schools would be needed to achieve adequate power for detecting a true effect with an effect size of g = .12 for student outcomes. However, 84 schools will be recruited in the two states of Georgia and South Carolina for adequate statistical power in testing the effects of the math professional development intervention on student outcomes to handle anticipated attrition at the school level.2 An even number of schools will be selected within each district to ensure operation of the matching strategy described below.
Power estimates for analyses of confirmatory student outcome (RQ1).
This study is conceived as comprising three levels, with students (Level-1) nested within classrooms (Level-2), within schools (Level-3). School-pairs will be treated as fixed effects in the model. The study team will create school-pairs within each district using an optimal bipartite propensity score model, constructed from a vector of school-level variables including prior year third grade achievement on the state math assessment, % students eligible for free-reduced lunch, % of African American students, % of English language learners, and total school enrollment. One member of each pair will be randomly assigned to the treatment condition.
Below is a list of assumptions and values used in conducting power analysis for the student outcome:
= .05 with a two-tailed test
Power = .80
2 = .05 (an estimate of teacher/classroom-level intra-class correlation)3
3 = .10 (an estimate of school-level intra-class correlation)4
R12 =.65 (proportion of variance at the student-level explained by student-level covariate)5
R22 =.70 (proportion of variance at the classroom-level explained by both school-level and student-level covariates)6
R32 =.75 (proportion of variance at the school-level explained by both school-level and student-level covariates)7
J = 3 fourth grade teachers per school8
n = 57 students per school on average (assuming 3 teachers/classrooms * 19 students per class after approximately 90% student participation rate [assuming 10% parent opt out] and subsequent 15% student attrition)9
Table G.1a below demonstrates the possible number of schools needed based on alternate assumptions about minimum detectable effect size (MDES).
Table G.1a – Power analysis for RQ1: Student impact analysis
Student Math Achievement |
MDES |
||
.11 |
.12 |
.14 |
|
Estimated Number of Schools
|
100 |
80 |
60 |
In the prior literature review, in the studies that had at least substantively important findings and met WWC criteria, the smallest effect size observed was g =.20 on student outcomes on the state assessment for grades 5-8 (Sample McMeeking et al., 2012). This study will be powered to detect effect sizes at least as small as the lowest observed effect size from those previous studies. To be conservative, the study will include a minimum of 80 schools10 (combined treatment and control) to detect an effect size as small as g = 0.12. While small, an MDES of g = 0.12 represents approximately one-third of the average annual growth from third to fourth grade (Bloom, Hill, Black, & Lipsey, 2008).
Given the limited research base on which to estimate both the ICCs and the R2 values, there is some risk that these values will vary in practice from our estimates. Table G.1b examines a range of values for both of these parameters. For these estimates it is assumed that we will recruit 84 schools blocked into pairs within district, to handle possible attrition. It is assumed that on average 3 teachers will participate, and that on average 19 students (of 25) will participate from each classroom.
Table G.1b - MDES with a range of R2 and ICC assumptions |
|||
|
ICC (2 ,3)* |
||
R2
(R12, R22, R32)* |
(.05, .10) |
(.10, .15) |
(.15, .20) |
(.65, .70, .75) |
.12 |
.15 |
.17 |
(.60, .65, .70) |
.13 |
.16 |
.18 |
(.55, .60, .65) |
.14 |
.17 |
.20 |
(.50, .55, .60) |
.15 |
.18 |
.21 |
*Note: Values in the tables represent MDES given a sample of N=80 schools with a 50%/50% allocation. R12 = proportion of variance at the student-level explained by student-level covariate R22 = proportion of variance at the classroom-level explained by both school-level and student-level covariates R32 = proportion of variance at the school-level explained by both school-level and student-level covariates 2 = estimate of teacher/classroom-level intra-class correlation 3 = estimate of school-level intra-class correlation
|
|||
This exercise reveals that even under very conservative estimates of both the ICCs and R2 parameters the maximum MDES is .21. This effect size is still within the range of possible impacts from a professional development intervention.
Power estimates for analyses of exploratory teacher outcomes (RQ2)
A power analysis was conducted to determine what MDES would be achieved at the teacher level, if the study were powered for student outcomes. See Table G.2 below. With a minimum sample of 80 schools11 (approximately 240 teachers), the MDES is estimated to be .33. Recent large-scale studies of math professional development at the seventh grade by Garet et al. (2010, 2011) did not result in any significant impacts on total teacher knowledge scores for the primary analytic sample. However in subsequent exploratory analyses using a pooled sample of teachers12, they found significant impacts on the specialized knowledge of mathematics (Hill, Rowan, & Ball, 2005) needed for teaching (effect size 0.28; p<0.02). If the proposed study were to be powered based on these exploratory impacts from the Garet et al. (2011) study, to attain an MDES of .28, 110 schools would need to be recruited with 330 teachers, 30 schools more than the minimum sample of schools required for student outcomes. Therefore, no attempt was made to power this study for teacher outcomes, as these are not of primary interest to Alliance stakeholders and too expensive to target in the context of this RCT.
Table G.2 – Power analysis for RQ2: Teacher outcomes
Teacher Outcomes |
MDES |
|
.28a |
.33 |
|
Estimated Number of Teachers |
330 |
240 |
Estimated Number of Schools (based on an assumption of 3 teachers per school) |
110 |
80 |
a Size of significant impact reported in Garet et al. (2010, 2011) for a measure of teacher knowledge.
The assumptions that were used to estimate the above MDES for teacher outcomes (RQ2) are listed below:
=.05
Power = .80
= .10 (an estimate of school-level intra-class correlation obtained from our earlier study of a professional development program)
R2 = .35 (based on an estimate pre-/post-test correlations of the Math Knowledge Test at both the teacher and school levels)
n = 3 teachers per school
Thus to recap, the study is being powered only to detect impacts at the student level. To detect a true effect with an effect size of .12 for student outcomes, a minimum of 80 schools will be needed. However, 84 schools will be recruited for adequate statistical power to handle possible attrition at the school level.13
Analytic Methods
Blocking and Random Assignment
After MOUs have been signed by district and school leaders and consent forms have been signed by participating teachers, schools will be randomly assigned to treatment and control conditions.
An even number of schools will be selected within each district to ensure 1:1 matching. The study team will create school pairs within each district based on an optimal bipartite propensity score model, constructed from a vector of school-level variables including prior year third grade achievement on the state math assessment, % students eligible for free-reduced lunch, % of African American students, % of English-language learners, and total school enrollment. The optmatch package (Hansen et. al., 2013) available for R will be used to conduct optimal 1:1 matching within each district using the method pairmatch. One school from each pair will be randomly assigned to the DMI condition. To ensure the objectivity of the study, research staff not otherwise engaged with the study will perform the randomization.
Specifications of the primary confirmatory impact analysis (RQ1)
Given that the data that will be used to address the research questions proposed for this study are of a nested nature (i.e., students nested within teachers and teachers nested within schools), hierarchical linear modeling (HLM) will be used to perform the main impact analyses. The HLM approach explicitly takes into account the nested data structure, and thus produces properly-computed standard errors for the impact estimates (Raudenbush & Bryk, 2002).
For the confirmatory analysis (RQ1), a three-level model will be used to assess the impact of teacher professional development on student outcomes, with students at level 1, schools at level 2, school-pairs at level 3. Given that no attempt is being made to generalize beyond the limited number of districts included in this multi-site (i.e., school) randomized trial, the blocking variable (school-pairs) will be treated as fixed effects rather than random effects in the impact analyses. The intercept of the teacher-level model, which represents the average teacher outcome for a given school, is modeled as a random effect at the school level and as a function of school pair-specific intervention effects (captured by a set of professional development-by-pair interactions) and pair fixed effects (captured by a set of school-pair dummy indicators).
A measure of fourth grade student achievement in fractions (TUF), under development for this study by the Center for Improving Learning of Fractions (2014), will serve as the outcome for the confirmatory analysis. Prior-year state assessment scores and demographics will be included at the student level and a vector of teacher background characteristics as covariates at the teacher level, respectively, to improve the statistical precision of the impact estimates.
Missing data
Following the most recent guidance from the WWC Procedures and Standards Handbook, v. 3.0 (2013), which states that “the WWC prefers analyses conducted on actual, observed data” (p. 16), only those students with a post-test score will be included in the analytic sample. However multiple imputation will be used to estimate missing pretest scores or values, so that the models may be estimated with a complete non-missing data matrix.
Multiple stochastic regression imputation will be used for missing pretest or covariate data to ensure that data is available for Intent-to-Treat analyses.14 Imputations of missing pretest or covariates will be conducted separately for both treatment and control units (i.e. students and teachers). No non-response weighting of individual cases will be done.
The RQ1 model will be specified as follows:
Level 1 – Student level.
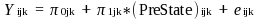
Where:
Yijk is the outcome for student i for teacher j in school k
(PreState)ijk is the prior year 3rd grade state assessment scores in mathematics for each student
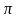 0jk
is
the average outcome of students with teacher j
in
school k
0jk
is
the average outcome of students with teacher j
in
school k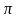 1jk
is
the association between pretest state
assessment
scores and student outcomes on the TUF
1jk
is
the association between pretest state
assessment
scores and student outcomes on the TUF
eijk is a random error associated with student i with teacher j in school k; eijk ~ N (0, σ2).
Level 2 - Teacher level.
 =
β00k
+ β01k*(X)jk
+ r0jk
=
β00k
+ β01k*(X)jk
+ r0jk
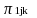 =
β10k
=
β10k
Where:
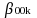 is
the average outcome of teachers in school j;
is
the average outcome of teachers in school j;
X is a vector of teacher background characteristics, including teaching experience, and credentials, grand-mean centered;
 is
the relationship between a vector of teacher background
characteristics and the outcome in school k; and
is
the relationship between a vector of teacher background
characteristics and the outcome in school k; andr0jk is a random error associated with teacher i in school j, rijk ~ N (0, σ2).
At Level 3 - School level.
β00k
=
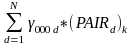 +
+
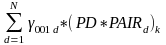 +
u00k
+
u00k
β01k = 010
β10k = 100
Where:
PD is the indicator variable for the intervention condition (1 = PD school, 0= control school)
PAIRk, k=1, 2, …, N, are dummy indicator variables representing the N schools in the sample
PD * PAIRd are N intervention-by-pair interaction terms
δk, k = 1, 2, …, N, represents the N pair intercepts
λk, k = 1, 2, …, N, represents the effect of PD for each of the N pairs
100 is the fixed effect representing the average student pretest across all schools
u0j is a random error associated with teacher j on teacher average outcome; u0j ~ N (0, τ00).
The three-level model for estimating student impacts will generate a pair-specific intervention impact (001d) for each of the N pairs. The overall treatment effect will be computed as the weighted average of pair-specific treatment effects, weighting each pair by the N of the treatment school.
In addition to the statistical significance of the intervention’s effects, the magnitude of the effects will also be gauged by computing the effect sizes (standardized mean difference, or Hedges’ g) associated with the impact estimates. Effects will be interpreted with an effect size equal to or greater than 0.25 as a “substantively important” effect (WWC Procedures and Standards Handbook, v. 3.0, 2013).
Specifications of the exploratory impact analyses (RQ2)
For exploratory analyses of DMI’s impact on teacher outcomes, a two-level HLM model will be used with teachers at level 1 and schools at level 2. Given that the school pairs do not represent a larger population of schools, school-pairs will be treated as fixed effects rather than random effects in the impact analyses. The intercept of the teacher-level model, which represents the average teacher outcome for a given school, is modeled as a random effect at the school level and as a function of pair-specific intervention effects (captured by a set of professional development-by-pair interactions) and pair fixed effects (captured by a set of pair dummy indicators). The specification of the model is as follows:
Level 1 - Teacher level.
Yij= β0j + β1j*(X)ij + rij
Where:
Yij is the outcome measure of teacher knowledge for teacher i in school j;
β0j is the average outcome of teachers in school j;
X is a vector of teacher background characteristics, including teaching experience, and credentials, grand-mean centered;
Β1j is the relationship between a vector of teacher background characteristics and teacher knowledge [MKT] and the outcome in school j; and
rij is a random error associated with teacher i in school j, rij ~ N (0, σ2).
Level 2 - School level.
β0j
=
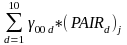 +
+
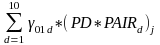 + u0j
+ u0j
β1j = 10
Where:
PAIRd , d = 1, 2, …, Nd, are dummy indicators representing the N pairs;
00d, d = 1, 2, …, Nd, represents the average teacher outcome in comparison schools in pair d;
PD* PAIRd,, d = 1, 2, … Nd, are a set of PD-by-pair interaction terms (PD = 1 for intervention schools, and 0 for comparison schools);
01d, d = 1, 2, … Nd, represents the difference in average teacher outcomes between intervention school and comparison school (i.e., intervention effect) in pair d;
10 is the average relationship between teacher background characteristics and the outcome across all schools; and
u0j is a random error associated with school j on school average teacher outcome; u0j ~ N (0, τ00).
The above model estimates a set of pair-specific intervention effect (01d). The overall intervention effect will be computed as the weighted average of pair-specific treatment effects, weighting each pair by the N of the treatment school.15 Again impact results will also be reported as a Hedges’ g and discussed in terms of statistical significance and discussed relative to the WWC’s benchmark for substantive importance (g ≥ 0.25).
Attrition, non-response, cross-overs, and participation
An intent-to-treat approach will be used for data collection, which means outcome data from all teachers and students in the original randomized study sample will be collected to the fullest extent possible.
Following the most recent guidance from the WWC Procedures and Standards Handbook, v. 3.0 (2013), which states that “the WWC prefers analyses conducted on actual, observed data” (p. 16), non-responders at post-test will be treated as attrition cases and not included in the analytic sample.
Included in the analytic sample (for RQ1) will be only those students with a complete and valid post-test. For the teacher knowledge outcome (RQ2) only teachers with knowledge test scores would be considered in the analytic sample (though students of teachers missing knowledge scores would be included in the analytic sample for RQ1 if the students have non-missing scores).
For missing pretest scores and covariate values, however, multiple imputation will be used so that a complete data matrix is available for analysis. Multiple imputation will be conducted separately for both treatment and control groups.16
Attrition rates will be calculated by overall sample and by treatment group. These findings will be compared to the WWC Standards for attrition that are current at the time of the final impact analysis. To examine differences in pretest scores and demographic characteristics, t-tests and chi-square tests will be used, comparing the sample of teachers and students at the time of randomization and the final analytic sample. These comparisons will be conducted by treatment group.
Crossovers
As a general rule, once students have been assigned to a condition (as a function of being initially enrolled in a school randomly assigned to that condition) they will remain in that condition for analytic purposes. Specifically, students who move during the study from a treatment classroom to a control classroom (in another school) will still be treated as if they were in the treatment condition for analytic purposes. Students who move during the study from a control classroom to a treatment classroom (in another school) will be treated as if they were in the control condition for analytic purposes. Students who move to a non-participating classroom within a participating school will be considered to be in the same condition as originally assigned and assessed. School-level MOUs will be written to include specification of these procedures.
All crossovers will be documented throughout the study and reported to provide context for the impact results. Students who move from a study school to a non-study school will not be tested and will be treated as attriting. This is because there would not be an MOU in place for testing students in schools outside of the study.
It is possible (though unlikely) that a teacher during the year may move to another school, either a school in another condition, or a non-participating school. Such teachers will still be assessed on teacher knowledge outcomes and treated analytically in the condition they were originally assigned.
Participation analysis
Two types of teacher participation will be examined. The first will be a comparison of teachers in study schools who signed consent forms for participation in the study versus those who did not. The second will be a comparison of teachers who completed 21 of the 24 hours of DMI sessions versus those who signed consent forms but completed fewer than 21 hours of DMI sessions. These groups will be compared using t-tests and chi-square tests on teacher demographics and teacher knowledge outcomes. For the first question, teacher demographics will be derived from school records for all teachers in participating schools.
For students, a waiver of active consent was granted by the IRB. However, should a substantial number of parents opt-out after receiving information of their school’s participation in the study demographics will be compared for those students whose parents allowed participation versus the demographics of all students in study schools. These school-wide demographics will be derived from school records.
The RQ1 impact analysis will be conducted as a sensitivity analysis, using only the subsample of teachers (and their students) who completed 21 or more hours of DMI sessions. This is analogous to a treatment-on-treated (TOT) analysis, where completion of 21 or more hours of DMI sessions is considered receiving intended treatment.
References
Bloom, H., Richburg-Hayes, L., & Black, A. (2007). Using covariates to improve precision for studies that randomize schools to evaluate educational interventions. Educational Evaluation and Policy Analysis, 29(1), 30-59.
Bloom, H. S., Hill, C. J., Black, A. R., & Lipsey, M. W. (2008). Performance trajectories and performance gaps as achievement effect-size benchmarks for educational interventions. Journal of Research on Educational Effectiveness, 1(4), 289-328. doi:10.1080/19345740802400072
Center for Improving Learning of Fractions. (2013). Center for Improving Learning of Fractions. Retrieved from https://sites.google.com/a/udel.edu/fractions/
Dong, N., & Maynard, R. (2013). PowerUp!: A tool for calculating minimum detectable effect sizes and minimum required sample sizes for experimental and quasi-experimental design studies. Journal of Research on Educational Effectiveness, 6(1), 24-67.
Garet, M., Wayne, A., Stancavage, F., Taylor, J., Eaton, M., Walters, K., . . . Doolittle, F. (2011). Middle School Mathematics Professional Development Impact Study: Findings After the Second Year of Implementation (NCEE 2011-4024). Washington, D.C.: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education.
Garet, M., Wayne, A., Stancavage, F., Taylor, J., Walters, K., Song, . . . Doolittle, F. (2010). Middle School Mathematics Professional Development Impact Sutdy: Findings After the First Year of Implementation (NCEE 2010-4009). Washington, D.C.: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education.
Gersten, R., Dimino, J., Jayanthi, M., & Haymond, K. (Manuscript in preparation ). The Impact of Participation in Teacher Study Groups: A Replication in First Grade Classrooms.
Hansen, B. B., Fredrickson, M., Buckner, J., Errickson, J., Solenberger, P., Bertsekas, D. P., & Tseng, P. (2013). Package ‘optmatch’. Author. Retrieved on November 21, 3013 from http://ftp.pregi.net/pub/pub/R/web/packages/optmatch/optmatch.pdf
Hedges, L., & Rhoads, C. (2009). Statistical Power Analysis in Education Research (NCSER 2010-3006). Washington, DC: National Center for Special Education Research Institute of Education Sciences, U.S. Department of Education. This report is available on the IES website at http://ies.ed.gov/ncser/
National Center for Educational Statistics. (2013). Common core of data. Retrieved from http://nces.ed.gov/ccd/
Raudenbush, S. W., & Bryk, A. S. (2002). Hierarchical linear models: Applications and data analysis methods (2nd ed.). Thousand Oaks, CA: Sage.
Raudenbush, S. W., Spybrook, J., Bloom, H., Congdon, R., Hill, C., & Martinez, A. (2011). Optimal Design Software for Multi-level and Longitudinal Research (Version 3.01) [Software]. Available from http://pikachu.harvard.edu/od/ or from www.wtgrantfoundation.org.
Sample McMeeking, L., Orsi, R., & Cobb, R. B. (2012). Effects of a teacher professional development program on the mathematics achievement of middle school students. Journal for Research in Mathematics Education, 43(2), 159-181.
StataCorp LP. (2013). STATA (Version 12.1) [Software]. Available from http://www.stata.com/stata12/
What Works Clearinghouse. (2013). What works clearinghouse: Procedures and standards handbook (Version 3.0). Retrieved from http://ies.ed.gov/ncee/wwc/pdf/reference_resources/wwc_procedures_v3_0_draft_standards_handbook.pdf
Wijekumar, K., Hitchcock, J., Turner, H., Lei, PW., & Peck, K. (2009). A Multisite Cluster Randomized Trial of the Effects of CompassLearning Odyssey® Math on the Math Achievement of Selected Grade 4 Students in the Mid-Atlantic Region (NCEE 2009-4068). Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education.
1 Power analyses were conducted using PowerUp! (Dong & Maynard, 2013) and cross-validated using Optimal Design software version 3.01 (Raudenbush et al., 2011). Equations were provided by Hedges and Rhoads (2009).
2 In a recent study of professional development for vocabulary instruction in 1st grade carried out by the PI of this proposal, the teacher attrition rate was low (5.2%) and was primarily due to the attrition of one school of 62.
3 Based on author estimates from a recent RCT implementation professional development in 62 schools (Gersten et al., manuscript in preparation).
4 Given that Bloom, Richburg-Hayes, and Black (2007) reported a range of .05-.18 for low-income schools and a range of .05-.16 for low-achieving schools in third grade reading, .10 would seem to be a reasonable assumption for schools targeted for this study.
5 Assuming.65 or greater correlation between the prior year state assessment and post-test administration of the TUF. Bloom et al. (2007) reported school-level R2 ranges of .48 to .83 for third grade math and from .47 to .73 for fifth grade math. They also reported student-level R2s ranging from .30 to .73 for third grade reading. Student-level R2 specifically in math was not reported.
6 Bloom et al. (2007) found school-level R2 ranging of .48 to .83 for third grade math and from .47 to .73 for fifth grade math in school-level random assignment studies. Wijekumar, Hitchcock, Turner, Lei, and Peck (2009) reported .73 for classroom-level R2 in a teacher random-assignment study using a math curriculum supplement.
7 Bloom et al. (2007) found school-level R2 ranging of .48 to .83 for third grade math and from .47 to .73 for fifth grade math in school-level random assignment studies. Wijekumar et al. (2009) reported .73 for classroom-level R2 in a teacher random-assignment study using a math curriculum supplement.
8 Estimated from the Common Core of Data (CCD) database maintained by the National Center for Education Statistics (2013) using 2010/11 school-level enrollment data. Assuming a 20% non-response rate to teacher enrollment in the study. In a recent study of professional development for vocabulary instruction in 1st grade carried out by the PI of this proposal, the teacher attrition rate was low (5.2%). The student attrition rate was 7.2%. Twice that rate is assumed for the current power analysis.
9 On average 97 students were enrolled in grade 4 in each public elementary school across Georgia and South Carolina. Assuming an average default class-size of 25.
10 The number of schools needed to detect an effect for this study is 80; however, we will over-recruit up to 84 schools to account for possible school-level attrition. We expect that 82 schools will remain in the study after attrition.
11 The number of schools needed to detect an effect for this study is 80; however, we will over-recruit up to 84 schools to account for possible school-level attrition. We expect that 82 schools will remain in the study after attrition.
12 The pooled sample of teachers combined three groups of teachers: teachers who were in the first year impact analysis only, teachers who were in the second year impact analysis only, and teachers who were in both years of the impact analysis. Teachers who participated in both the first and second year were represented in the data-file twice, once for each year.
13 The number of schools needed to detect an effect for this study is 80; however, we will over-recruit up to 84 schools to account for possible school-level attrition. We expect that 82 schools will remain in the study after attrition.
14 This will be accomplished using the mi procedures incorporated in STATA version 12.1 (StataCorp LP, 2013).
15 The sample size-weighted average effect will be similar to a simple average effect if the sample size or the intervention effect is similar across the districts.
16 Multiple imputation will be accomplished through the use of the mi procedures incorporated in STATA version 12.1 (StataCorp LP, 2013) using 20 imputations. Imputations of missing pretest or covariates will be conducted separately for both treatment and control units (i.e. students and teachers). No weighting of individual cases will be done.
L
-
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | Karen Denbroeder |
| File Modified | 0000-00-00 |
| File Created | 2021-01-27 |
© 2025 OMB.report | Privacy Policy