Att_1850-0877 v3 4754 ARRA Evaluation Part B 2-7-12
Att_1850-0877 v3 4754 ARRA Evaluation Part B 2-7-12.docx
Integrated Evaluation of American Recovery and Reinvestment Act (ARRA) Funding, Implementation and Outcomes
OMB: 1850-0877
Integrated Evaluation of ARRA Funding, Implementation and Outcomes
Statement for Paperwork Reduction Act Submission
PART B: Collection of Information Employing Statistical Methods
Contract ED-IES-10-CO-0042
February 2012
Page
Part B: Collection of Information Employing Statistical Methods 1
B.1 Respondent Universe and Sampling Methods 3
B.2 Information Collection Procedures 5
B.3 Methods to Maximize Response Rates 18
B.5 Individuals Consulted on Statistical Aspects of Design 19
Part B: Collection of Information Employing Statistical
This package is the third of three for the Integrated Evaluation of ARRA Funding, Implementation, and Outcomes. Our initial request sought approval for execution of a sampling plan and recruitment of the selected sites. Approval for these activities was received on January 13, 2011 (see 1850-0877 v.1 (4385)). Our second request sought approval for an initial round of data collection to include surveys of all states and a nationally representative sample of districts and schools in spring 2011. Approval for baseline data collection was received on April 5, 2011 (see 1850-0877). This third and final package is requesting approval to conduct follow up surveys with the same respondents in 2012 that were sampled and surveyed in 2011.
Please note that this OMB package is identical to the OMB package that was approved for baseline data collection – with the overall purpose of the study and primary data collection activities remaining unchanged – with a few exceptions that are discussed below:
(1) We will no longer be conducting the final round of follow up surveys planned for 2013. This decision is related to a newly awarded IES contract focused on examining the implementation of Title I/II program initiatives and IES’ interest in coordinating efforts to reduce burden on state, district, and school respondents. Like the ARRA Evaluation, the Title I/II study will also involve nationally representative surveys examining the implementation of reform efforts. Therefore, IES is coordinating the two studies so that they are mutually informative and will avoid duplication of efforts by fielding surveys for the Title I/II study only in 2013. This will allow IES to track key reform activities over time, while (a) avoiding the potential difficulty that might arise when seeking high response rates to a survey focused on ARRA years after the funds were distributed and (b) avoiding undue burden for respondents.
(2) Since we will not be conducting the final round of data collection, a set of outcomes analyses that were described in this part -- Part B -- of the second OMB package will not be conducted. Although we will examine relationships between ARRA funding and the implementation of reforms thought to promote achievement, it will not be feasible to examine more direct relationships between funding and achievement.
(3) Finally, we will not be conducting polls in fall/winter 2011 and in fall/winter 2012. This decision is a based on the amount of information captured by the study’s baseline and follow up surveys and the desire to reduce burden for respondents.
Changes to this third OMB package (as compared to the second submission), which all stem from the decisions discussed above, are highlighted in yellow.
Introduction
On February 17, 2009, President Obama signed the American Recovery and Reinvestment Act (ARRA) into law (Pub. L. 111-5). ARRA provides an unprecedented $100 billion of additional funding for the U.S. Department of Education (ED) to administer. While the initial goal of this money is to deliver emergency education funding to states, ARRA is also being used as an opportunity to spur innovation and reform at different levels of the U.S. educational system. Specifically, ARRA requires those receiving grant funds to commit to four core reforms: (1) adopting rigorous college-ready and career ready standards and high quality assessments, (2) establishing data systems and using data to improve performance, (3) increasing teacher effectiveness and the equitable distribution of effective teachers, and (4) turning around the lowest performing schools. Investment in these innovative strategies is intended to lead to improved results for students, long-term gains in school and local education agency (LEA) capacity for success, and increased productivity and effectiveness.
The education component of ARRA consists of several grant programs targeting states and LEAs and, in some cases, consortia led by non-profit organizations. The programs under ARRA fall into three general categories: (1) existing programs that received an infusion of funds (e.g., Individuals with Disabilities Education Act, Parts B & C; Title I; State Educational Technology grants; Statewide Longitudinal Data Systems grants); (2) a new program intended mainly for economic stabilization (i.e., State Fiscal Stabilization Fund); and (3) newly created programs that are reform-oriented in nature. Due to the number and scope of these programs, a large proportion of districts and schools across the country will get some ARRA funding. In turn, ARRA represents a unique opportunity to encourage the adoption of school improvement focused reforms and to learn from reform initiatives as they take place.
Although ARRA funds are being disbursed through different grant programs, their goals and strategies are complementary if not overlapping, as are the likely recipients of the funds. For this reason, an evaluative approach where data collection and analysis occurs across grant programs (i.e., it is “integrated”), rather than separately for each set of grantees will not only reduce respondent burden but will also provide critical information about the effect of ARRA as a whole.
Participation in the evaluation is required to maintain a benefit. The required participation can be found in EDGAR regulations sections 75.591 and 75.592 (see below). This expectation is communicated with states and districts receiving ED grants letting them know that they do have an obligation to cooperate with evaluation studies.
§ 75.591 Federal evaluation—cooperation by a grantee.
A grantee shall cooperate in any evaluation of the program by the Secretary.
(Authority: 20 U.S.C. 1221e–3 and 3474)
[45 FR 86297, Dec. 30, 1980]
§ 75.592 Federal evaluation—satisfying requirement for grantee evaluation.
If a grantee cooperates in a Federal evaluation of a program, the Secretary may determine that the
grantee meets the evaluation requirements of the program, including §75.590.
(Authority: 20 U.S.C. 1221e–3 and 3474)
Overview of the Study
The Integrated Evaluation of ARRA Funding, Implementation and Outcomes is being conducted under the Institute of Education Sciences (IES), ED’s independent research and evaluation arm. The study is one of several that IES will carry out to examine ARRA’s effects on education (see Exhibit 1).
Exhibit 1. IES Evaluation of ARRA’s Effects on Education
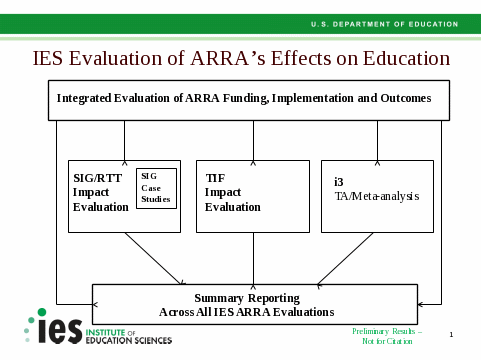
The Integrated Evaluation is designed to assess how ARRA efforts are unfolding over time and is therefore primarily descriptive. While information will be gathered on many of the grant programs, the evaluation will focus primarily on the reform-oriented programs (e.g., Race to the Top (RTT), Title I School Improvement Grants (SIG), Investing in Innovation (i3), and the Teacher Incentive Fund (TIF)) since those are of the greatest policy interest.1 The study will support the various impact evaluations IES is conducting by providing critical context for those strategies being rigorously investigated – e.g., by documenting the relative frequency with which they are being implemented across the country, whether they are unique to the particular grant programs, and how they are being combined with other reform approaches.
To achieve these objectives, the Integrated Evaluation will draw heavily on existing information (grant funding allocations, district and school outcomes databases, performance reporting where available) and administer new surveys to all 50 states and to a nationally representative survey of districts and schools. . The first year of this two year survey was conducted in the spring 2011 and the second year of the study will be in spring 2012.
.
B.1 Respondent Universe and Sampling Methods
We will administer surveys to 50 states and the District of Columbia; a nationally representative sample of 1,700 school districts; and a nationally representative of 3,800 schools. Our initial request sought approval for execution of a sampling plan and recruitment of the selected sites. Approval for these activities was received on January 13, 2011 (see 1850-0877 v.1 (4385)).
The detailed description of the assembly of a universe frame and sampling plan, from our original package, is inserted below.
We will administer surveys to states, school districts, and schools. The assembly of a universe frame and sampling plan for each is described below.
State Surveys
We will survey all 50 states and the District of Columbia; there is no sampling proposed for the state survey.
School District Surveys
We will construct a respondent pool and implement a sampling approach for each of the following:
A nationally representative sample of districts, with oversampling of certain ARRA program grantees, in order to track funding and implementation progress at this organizational level; and
A small nationally representative subsample of the nationally representative district sample, in order to obtain information on pressing policy and implementation concerns that might help ED refine technical assistance and legislative plans.
Nationally representative sample of school districts
We will draw a nationally representative sample of districts because ARRA is intended to stimulate broad system change and because, looking across all the ARRA programs, the expected recipients of funds are likely to include most districts. We anticipate that the amount and degree of ARRA funding will vary considerably, but most districts will receive at least some funding. A nationally representative sample then should provide a district sample with a range of funding levels. This sample will be augmented with a sample of districts that are grantees or subgrantees from two of the competitive ARRA programs – Race to the Top (RTT) and the Teacher Incentive Fund cohort 3 (TIF3) – because there is considerable policy interest in the types of reforms being undertaken in school districts that receive RTT and TIF funds in comparison to school districts that do not receive these funds, which are focused on the assurances of educator effectiveness and turning around low performing schools.
We will draw a probability proportionate to size (PPS) sample of districts, with number of students as the measure of size. This PPS sample design will be most efficient for district level estimators which are weighted by number of students. Using PPS designs is the most common and cost effective approach for selecting nationally representative samples.
To construct the sampling frame, we will use data from multiple sources, including (1) the National Center for Education Statistics’ Common Core of Data (CCD) for the universe of school districts, number of students, urbanicity, and poverty status; and (2) lists from ED on the TIF3 grantees.
We will draw a sample of 1,700 school districts out of 16,398 school districts.
School Surveys
We will construct a respondent pool and implement a sampling approach for:
A nationally representative sample of schools, with oversampling of schools likely to be affected by ARRA programs, in order to track funding and implementation progress at this organizational level.
To construct the sampling frame, we will use data from multiple sources, including (1) the CCD for the universe of schools (within the sampled school districts) and school level; (2) applications for the School Improvement Grant (SIG) program to identify lists of schools identified as persistently low achieving (PLA); and (3) EDFacts, maintained by ED, for the lists of schools identified as in need of improvement (SINI) under ESEA.
We will draw a sample of 3,800 schools nested within the nationally representative sample of 1,700 school districts. (The universe of schools is 100,640.)
B.2 Information Collection Procedures
Our initial request sought approval for execution of a sampling plan and recruitment of the selected sites. Approval for these activities was received on January 13, 2011 (see 1850-0877 v.1 (4385)). Part B (Section B.2) of the Supporting Statement for that original package included a detailed description of notification of the sample and our recruitment of the sample. Below, we describe our plan for communicating with the sample and administering the surveys in spring 2012.
Communicating in Spring 2012. We will use both telephone and email to confirm that state and district liaisons are still employed and acting in this capacity. If not, we will work with the states and districts to obtain new liaisons. We will remind the state and district respondents of their obligation to participate in evaluations of programs for which they receive federal fundning. We will renew any necessary research applications.
Administering Surveys in Spring 2012. We will email a cover letter to the states, districts, and schools. The cover letter will explain how to complete the survey. For state surveys, these emails will explain that the attached survey can be completed as an electronic document and returned electronically or printed and completed as a paper-and-pencil instrument to be returned by fax or mail. The district emails will be sent to the study liaison and the school emails will be sent to the principals. The district and school cover letters will clearly explain that respondents have two options for responding to the survey: as a web-based instrument or as a paper-and-pencil instrument. They will also include the survey URL and login ID for responding to the survey as a web-based instrument. All letters will include a toll-free number and a study email address for respondents’ questions and technical support.
Nonresponse Followup. We will initiate several forms of follow-up contacts with state, district and school respondents who have not responded to our communication. We will use a combination of reminder postcards, emails and follow up letters to encourage respondents to complete the surveys. The project management system developed for this study will be the primary tool for monitoring whether surveys have been initiated. After 10 days, we will send an email message (or postcard for those without email) to all nonresponders indicating that we have not received a completed survey and encouraging them to submit one soon. Within 7 business days of this first follow up we will mail nonrespondents a hard copy package including all materials in the initial mailing. Ten days after the second followup, we will telephone the remaining nonrespondents to ask that they complete the survey and offer them the option to answer they survey by phone, either at that time or at time to be scheduled during the call.
In spring 2011, we obtained a response rate of 100 percent at the state level, 89 percent (weighted) at the school district level, and 77 percent (weighted) at the school level. For spring 2012, we expect to obtain a 100 percent response rate at the state level, and 80 perecent at the school district and school levels.
B2.1 Statistical Methodology for Stratification and Sample Selection
Our initial request sought approval for execution of a sampling plan and recruitment of the selected sites. Approval for these activities was received on January 13, 2011 (see 1850-0877 v.1 (4385)).
The detailed description of our statistical methodology for stratification and sample selection, from our original package, is inserted below..
Nationally representative sample of school districts
As discussed in B.1, we will draw a nationally representative sample of 1,700 school districts from the 50 states and the District of Columbia. One analytic interest is in comparing the activities of districts with large amounts of ARRA funding (per pupil) with similar districts with lesser (or no) funding. The amount and degree of ARRA funding we anticipate will vary considerably, but most districts will receive at least some funding. A nationally representative sample then should provide a district sample with a range of funding levels.
The district frame is based on the 2008-09 National Center for Education Statistics’ Common Core of Data (CCD) frame, as processed through National Assessment of Educational Progress (NAEP) macros to purge entities that are not in scope (e.g., administrative districts, district consortiums, entities devoted to auxiliary educational services, etc.), as well as a canvassing of new districts from the preliminary 2009-10 CCD frame (only districts with positive enrollments on the CCD frame, with other out-of-scope entities purged out). All school districts and independent charter districts with at least one eligible school and at least one enrolled student will be included in the frame.2
There will be a probability proportionate size (PPS) sample of districts, with number of students as the measure of size. Given the evaluation’s goal of focusing on ARRA funded reform efforts, the major strata will ensure that districts from Race to the Top (RTT) states are represented to reflect their actual population values. The strata include:
RTT winning states (Delaware, District of Columbia, Florida, Georgia, Hawaii, Maryland, Massachusetts, New York, North Carolina, Ohio, Rhode Island, Tennessee);
RTT finalist states (Arizona, California, Colorado, Illinois, Kentucky, Louisiana, New Jersey, Pennsylvania, South Carolina); and
All other states.
The RTT finalist states are states which were round two finalists for Race to the Top funding but did not win. These states should be similar in many ways to the RTT states and can, therefore, provide a key comparison group for analysis. We plan to oversample high-poverty districts. We are defining districts to be high-poverty if they have greater than 16.7 percent of 5 to 17 year olds in poverty, according to estimates for 2008 from the Small Area Income and Poverty Estimate Program (SAIPE).3
The oversampling factor for high-poverty districts will be a factor of 2.4 Table 1 presents expected student percentages for the three district strata crossed by high-poverty status.5 The measure of size for each stratum is proportional to two times the percentage of students for the high-poverty strata, and is proportional to the percentage of students for the low-poverty strata. The allocated sample size is based on this measure of size. We expect 20 percent attrition due to nonresponse. Sample sizes after this expected attrition are presented in the last column to the right.
Table 1. District Sample Design: RTT and Poverty Strata Allocations
Stratum |
Poverty stratum |
Estimated student count (in 1000s) |
Percent of students |
Percent of measure of size |
Allocation propor-tional to estimated measure of size |
Sample size after attrition |
|
|
|
|
|
|
|
RTT Winners |
High |
5,746 |
11.72% |
16.36% |
278 |
222 |
RTT Winners |
Low |
7,797 |
15.90% |
11.10% |
189 |
151 |
RTT Winners |
Total |
13,543 |
27.61% |
27.45% |
467 |
373 |
|
|
|
|
|
|
|
RTT Finalists |
High |
7,269 |
14.82% |
20.69% |
352 |
281 |
RTT Finalists |
Low |
8,177 |
16.67% |
11.64% |
198 |
158 |
RTT Finalists |
Total |
15,447 |
31.49% |
32.33% |
550 |
440 |
|
|
|
|
|
|
|
Remainder States |
High |
8,196 |
16.71% |
23.33% |
397 |
317 |
Remainder States |
Low |
11,862 |
24.19% |
16.88% |
287 |
230 |
Remainder States |
Total |
20,058 |
40.90% |
40.21% |
684 |
547 |
|
|
|
|
|
|
|
Total |
|
49,048 |
100.00% |
100.00% |
1,700 |
1,360 |
Table 2 presents calculations of normalized standard errors for the two poverty strata, and for the national estimator, based on a completely proportional sample design (no oversampling of high-poverty districts) and the proposed sample design which includes oversampling of high-poverty districts. The middle columns present sample sizes after expected attrition from 20 percent nonresponse and normalized standard errors from a strictly proportional allocation. The final three columns to the right present expected sample sizes after expected attrition and normalized standard errors under the proposed sample design of oversampling high-poverty districts by a factor of 2 (so that the high-poverty districts receive 2/3 of the sample allocation). The normalized standard errors are the standard error as a fraction of the population standard deviation for a particular characteristic of interest at the population level.6 For example, a normalized standard error of 2.87 percent means that if the population standard deviation for a characteristic is 100, then the national estimator standard error for this characteristic will be 2.87.
As can be seen, under the proposed design the normalized standard error for high-poverty districts is much lower as compared to proportional allocation. The normalized standard error for low-poverty districts is much higher for the proposed design as compared to proportional allocation, but high-poverty districts are of particular interest for this study. For national estimators, the normalized standard error under the proposed design is a little bit higher than that for a proportional allocation design. This is a small loss of efficiency for the proposed national design in order to achieve a much better result for high-poverty districts. Given the importance of high-poverty districts in this study, this is a tradeoff worth making.
Table 2. Normalized Standard Errors for the Two Poverty Strata
|
Proportional sample design |
Proposed sample design |
|||||
District Stratum |
Estimated student count (in 1000s) |
Percent of students |
Propor-tional sample size (after attrition) |
Norma-lized standard error |
Percent of measure of size |
Over-sampling design sample size after attrition |
Norma-lized standard error |
|
|
|
|
|
|
|
|
High-poverty |
21,211 |
43.25% |
588 |
4.12% |
60.38% |
821 |
3.49% |
Low-poverty |
27,837 |
56.75% |
772 |
3.60% |
39.62% |
539 |
4.31% |
Total |
49,048 |
100.00% |
1,360 |
2.71% |
100.00% |
1,360 |
2.87% |
Table 3 presents results for the three primary strata comparing proportional allocation to the proposed design. In this case, a normalized standard error is only presented for the proposed design and a design effect is included, which is equal to the square of the ratio of the normalized standard error of the proposed design to that of a proportional allocation design within each primary stratum. These design effects for the primary strata are very reasonable again as a cost of improving standard errors for the high-poverty strata within each primary stratum.
Table 3. Normalized Standard Errors for the Three Primary Strata
Stratum |
Poverty stratum |
Percent of students |
Sample size after attrition |
Normalized standard error |
Design effect |
|
|
|
|
|
|
RTT Winners |
High |
42.43% |
222 |
6.70% |
1 |
RTT Winners |
Low |
57.57% |
151 |
8.14% |
1 |
RTT Winners |
Total |
100.00% |
373 |
5.48% |
1.122 |
|
|
|
|
|
|
RTT Finalists |
High |
47.06% |
281 |
5.96% |
1 |
RTT Finalists |
Low |
52.94% |
158 |
7.95% |
1 |
RTT Finalists |
Total |
100.00% |
440 |
5.06% |
1.125 |
|
|
|
|
|
|
Remainder States |
High |
40.86% |
317 |
5.61% |
1 |
Remainder States |
Low |
59.14% |
230 |
6.60% |
1 |
Remainder States |
Total |
100.00% |
547 |
4.53% |
1.121 |
Within the RTT stratum, we will stratify first by state to be sure that each RTT winning state had proportional representation. Within the RTT finalist stratum and the remainder stratum, we will stratify first by Census Region to be sure we have geographic representation. Table 4 below presents percentages for each RTT state as a share of all RTT states, as a fraction of student enrollment and as a fraction of the total measure of size (with high-poverty districts doubled as compared to low-poverty districts). The allocated sample size is the overall RTT state sample size of 467 multiplied by the estimated measure of size percentage. The ‘total CCD districts’ is a count of school districts for the state from our district frame. In two cases, the allocated district sample size exceeds the total CCD district count. Hawaii has only one single district covering the entire state, and this will be taken with certainty. Florida and Maryland have a small number of districts given its population, and all districts will be taken in Florida and Maryland as well. Subtracting out the district totals for Florida, Maryland and Hawaii, the remaining sample is 368 (467 minus 99). This sample is reallocated across the remaining RTT states to complete the assigned sample size calculation, as given in the rightmost column of Table 4.
Table 4. Estimated Shares and Expected Sample Sizes for the RTT States
State |
Estimated students (in 1000s) |
Percent of students |
Estimated percent of measure of size |
Allocated sample size |
Total CCD districts |
Assigned sample size |
|
|
|
|
|
|
|
Delaware |
125 |
0.9% |
0.8% |
4 |
37 |
4 |
District of Columbia |
69 |
0.5% |
0.7% |
3 |
56 |
3 |
Florida |
2,630 |
19.4% |
17.7% |
83 |
73 |
73 |
Georgia |
1,656 |
12.2% |
12.9% |
60 |
186 |
62 |
Hawaii |
179 |
1.3% |
0.9% |
4 |
1 |
1 |
Maryland |
844 |
6.2% |
4.9% |
23 |
25 |
25 |
Massachusetts |
958 |
7.1% |
6.1% |
29 |
392 |
29 |
New York |
2,658 |
19.6% |
21.5% |
101 |
855 |
104 |
North Carolina |
1,489 |
11.0% |
12.0% |
56 |
211 |
58 |
Ohio |
1,817 |
13.4% |
13.2% |
62 |
942 |
63 |
Rhode Island |
145 |
1.1% |
1.0% |
5 |
51 |
5 |
Tennessee |
972 |
7.2% |
8.2% |
38 |
140 |
39 |
Total |
13,543 |
100.0% |
100.0% |
467 |
2969 |
467 |
Table 5 presents similar computations for the RTT finalist and the remainder stratum. Sample sizes after expected nonresponse attrition are also presented. In this case, the strata are by Census Region.
Table 5. Estimated Shares and Expected Sample Sizes for the RTT Finalist and Remainder Stratum States, by Census Region Strata
Stratum |
Census Region |
Estimated student count (in 1000s) |
Percent of students |
Percent of measure of size |
Projected sample size |
Projected sample size after attrition |
|
|
|
|
|
|
|
RTT Finalists |
Northeast |
3,099 |
20.06% |
17.94% |
99 |
79 |
RTT Finalists |
Central |
2,120 |
13.72% |
13.37% |
74 |
59 |
RTT Finalists |
South |
2,075 |
13.43% |
15.86% |
87 |
70 |
RTT Finalists |
West |
8,153 |
52.78% |
52.82% |
291 |
232 |
RTT Finalists |
Total |
15,447 |
100.00% |
100.0% |
550 |
440 |
|
|
|
|
|
|
|
Remainder Stratum |
Northeast |
1,048 |
5.23% |
4.64% |
32 |
25 |
Remainder Stratum |
Central |
6,790 |
33.85% |
33.11% |
226 |
181 |
Remainder Stratum |
South |
8,624 |
42.99% |
45.41% |
311 |
248 |
Remainder Stratum |
West |
3,597 |
17.93% |
16.85% |
115 |
92 |
Remainder Stratum |
Total |
20,058 |
100.00% |
100.0% |
684 |
547 |
The RTT/geography strata (state within the RTT stratum, and Census Region within the RTT finalists and the remainder strata) are the ‘explicit strata:’ the sample sizes are set exactly for each of these strata. The remaining district stratification is ‘implicit:’ it is implemented by a serpentine sorting7 within a hierarchy, followed by a systematic sample. Urbanicity stratum is the implicit stratifier within the RTT state stratum and the non-RTT Census Region strata (1—Central City, 2—Urban Fringe, 3—Town, 4—Rural). Urbanicity for each district is provided on the CCD district frame.
Details
of District Frame Sampling: Stratification and Oversampling
The following districts will be certainty selections (included automatically in the sample with probability of selection 1):
District of Columbia Public Schools;
The Hawaii Unified Public School District;
All districts in the states of Florida and Maryland; and
All other districts with measures of size exceeding the sampling interval at any point in the iterative process (see below).
Write
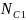 as the total number of certainty districts from bullets 1 through 3.
The initial measure of size for PPS district sampling is computed as
follows. Write
as the total number of certainty districts from bullets 1 through 3.
The initial measure of size for PPS district sampling is computed as
follows. Write
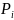 as the total number of students in district i
and write
as the total number of students in district i
and write
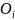 as the oversampling factor for district i,.
The values of
as the oversampling factor for district i,.
The values of
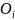 are given in Table 6 below. Note, given the evaluation’s focus
on reform efforts, the Teacher Incentive Fund (TIF) districts will be
oversampled to make sure that at least 70 of these districts are in
the district sample.
are given in Table 6 below. Note, given the evaluation’s focus
on reform efforts, the Teacher Incentive Fund (TIF) districts will be
oversampled to make sure that at least 70 of these districts are in
the district sample.
Table 6. Oversampling Factors by Poverty and TIF Stratum
Poverty Stratum |
TIF Stratum |
Oversampling Factor |
Low Poverty |
TIF |
1.7 |
Low Poverty |
nonTIF |
1 |
High Poverty |
TIF |
3.4 |
High Poverty |
nonTIF |
2 |
The
measure of size for each district is proportional to
 .
We assign the remaining certainty districts by an iterative process
in which each iteration is as follows:
.
We assign the remaining certainty districts by an iterative process
in which each iteration is as follows:
remove the certainty districts already assigned (the original
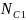 plus any certainty districts assigned in earlier iterations),
plus any certainty districts assigned in earlier iterations),
compute a sampling interval equal to the summation of
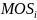 over the districts left on the frame (those not removed as
certainty districts), divided by 1700 minus the total number of
currently assigned certainty districts;
over the districts left on the frame (those not removed as
certainty districts), divided by 1700 minus the total number of
currently assigned certainty districts;designate as certainties any districts whose
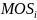 exceeds the current sampling interval, and
exceeds the current sampling interval, andreturn to step (i).
The
iteration stops when there are no further certainties generated.
Write
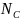 as the final number of certainty districts, and SAMP
as the final sampling interval. The probability of selection of each
district on the noncertainty frame is
as the final number of certainty districts, and SAMP
as the final sampling interval. The probability of selection of each
district on the noncertainty frame is
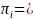 )*
)*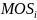 /SAMP.
Note that the summation of
/SAMP.
Note that the summation of
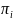 is equal to the noncertainty sample size
is equal to the noncertainty sample size
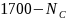 .
.
The
sampling of noncertainty districts will be a systematic sampling
process, using the
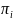 as the probabilities of selection, and SAMP
as the sampling interval. The ordering of districts for this
systematic sample will be hierarchical. The levels of the hierarchy
are as follows:
as the probabilities of selection, and SAMP
as the sampling interval. The ordering of districts for this
systematic sample will be hierarchical. The levels of the hierarchy
are as follows:
RTT winner/ RTT finalist/ remainder state;
Geography (state within RTT winner; Census Region for RTT finalist and remainder state);
Multi-School/ One-School District Status;8
Charter/Regular Districts (within One-School Districts only);
TIF/ non TIF status;
Urbanicity (Central City; Urban Fringe; Town; Rural);
Size.
Size will be ordered in a serpentine fashion (largest to smallest, smallest to largest, largest to smallest, etc.), within urbanicity, urbanicity will be ordered in a serpentine fashion within TIF status (central city to rural, rural to central city, central city to rural, etc.), and TIF status will be ordered in a serpentine fashion with Multi-School/ One-school (TIF to non TIF, non TIF to TIF, etc.). Multi-school/One-school status will be ordered in a serpentine fashion within the geographic strata. Census Region will be ordered in a serpentine fashion within the RTT finalist and remainder state strata.
Details of District Frame Sampling: Assignment to the High Poverty Stratum
The high poverty stratum is defined by SAIPE estimates of percentages of 5 to 17 year old children in poverty for the school district. We will compute the mean value of this percentage over all districts in the U.S., and this mean value will become the cutoff.9 Districts with percentages lower than the cutoff will be designated ‘low poverty’ and districts with percentages higher than the cutoff will be designated ‘high poverty.’ Independent districts such as charter school districts will be associated with the public school district that they are associated with geographically, as only the primary geographically-based public school districts have poverty estimates from SAIPE.
Details of District Frame Sampling: One-School Districts
Any districts with only one school will have a sampling rate set to be 1/4 of the sampling rate they would otherwise receive. We estimate that these districts represent roughly 2 percent of the student population, so without undersampling the district sample would have about 40 sampled districts. (Having districts with only one school is problematic for analyses such as Hierarchical Linear Modeling.) With the undersampling, the expected number will be reduced to a number in the range of 10. These districts will be a separate strata, to control the sample size (so that we do not get too few or too many inadvertently). Even with this undersampling they will still be represented correctly in the population, as their weights will reflect their reduced probabilities of selection (the weights will be 4 times larger than they would otherwise be), but we will have fewer of these districts. This method of undersampling is similar to that done in the National Assessment of Educational Progress for schools with very small numbers of students.
Districts with Persistently Lowest Achieving (PLA) Schools
As discussed in the School Sample Design section below, we have a target sample size of Persistently Lowest Achieving (PLA) schools of 570. This is being drawn from an estimated set of roughly 2,250 of these schools. Many of these schools are in high-poverty districts, so the oversampling of high-poverty districts may yield a large enough set of these schools from which to draw our target sample. Our criterion will be that we wish to guarantee that there will be only a 5 percent chance (or less) that there will be less than 570 PLA schools in the sampled district frame. In order to achieve this goal, it may be necessary to have an extra oversampling rate for districts with at least one PLA school. This oversampling rate, if necessary, will be set in such a way to guarantee this lower bound of 570 expected PLA schools, with at least 95 percent certainty. All districts with at least one PLA school will receive an equal oversampling factor attached to their measure of size (in addition to other factors for high-poverty status and/or TIF status). All of this can only be finalized after the district and school frames are complete, but the sample design will be adjusted up front to make sure that the goals of the study can be achieved,10
Nationally representative sample of schools
The school sample is a two-phase sample of 3,800 schools, nesting within the sampled districts. We want the school sample to be balanced at the sampled district level, in that the sample sizes are close to the desired sample sizes (e.g., if the expected sample size is 3, then the actual sample size also be three, or at least in the range 2 through 4). This is easy to achieve if districts are the only strata, but we also want balance in terms of:
School level: elementary, middle, and high schools (which is important in light of the current emphasis on high school reform);
School performance status: PLA schools, other schools in need of improvement (SINI), and all other schools; and
School size: small, medium, and large (which allows us to examine whether smaller schools, for example, have the resources to undertake the same types of reform strategies as larger schools).
Overall, this is a multi-dimensional stratification structure. With an average sample size of only 2.2 schools per district (3,800 divided by 1,700), balancing on all of these dimensions simultaneously will be difficult using traditional stratification. A relatively new sampling technique which we propose is called ‘balanced sampling,’ or ‘cube sampling,’ developed in Europe and used, for example, in French Census rotation groups (see for example Deville and Tillé 200411). We will confirm that the algorithm is providing random samples with the desired properties. If Deville and Tillé’s method does not achieve the goal, other methods will be utilized to achieve the desired stratification, or an approximation thereof.12
PLA schools will be oversampled due to ARRA’s focus on turning around low performing schools. Our goal is that 15 percent of the sampled schools should be PLA. After checking expected sample sizes, we will define an oversampling factor if it is necessary. Table 7 presents preliminary information about counts of PLA schools and SINI non PLA schools. Our target sample percentages and sample sizes are given.
Oversampling factors will be defined in order to achieve these goals. It should be noted that we expect the oversampling of high-poverty districts to generate a large number of PLA schools, as we expect most PLA schools to be in high-poverty districts. The oversampling factor then necessary to achieve the 15 percent sample size goal may not be large.
Table 7. Estimated Percentages and Target Sample Sizes by School Performance Status
School Performance Status |
School count |
Percent of schools |
Expected sample size propor-tional allocation |
Target sample percent of schools |
Target school sample size |
|
|
|
|
|
|
PLA |
2,248 |
2.40% |
91 |
15.0% |
570 |
SINI non PLA |
12,165 |
12.96% |
493 |
15.0% |
570 |
Other |
79,418 |
84.64% |
3,216 |
70.0% |
2,660 |
Total |
93,831 |
100.0% |
3,800 |
100.0% |
3,800 |
Table 8 presents similar calculations by school grade span, which we define as follows, following the CCD definition:
elementary is defined to have a low grade of PK through 3rd grade, and a high grade of PK through 8th grade;
middle is defined to have a low grade of 4th through 7th grade, and a high grade of 4th through 9th grade;
high school is defined to have a low grade of 7th through 12th, and a high grade of 12th only; and
other schools is defined to include all other schools.
Table 8. Estimated percentages and target sample sizes by school grade span
School Grade Span |
Estimated students (in 1000s) |
Percent of total |
Estimated measure of size (in 1000s) |
Percent of total |
Expected sample size |
Expected sample size after attrition |
Elementary |
21,058 |
43.25% |
33,021 |
44.95% |
1,708 |
1,366 |
Middle |
9,292 |
19.08% |
14,015 |
19.08% |
725 |
580 |
High |
13,655 |
28.04% |
18,839 |
25.64% |
975 |
780 |
Other schools |
4,686 |
9.62% |
7,586 |
10.33% |
392 |
314 |
Total |
48,691 |
100.00% |
73,461 |
100.00% |
3,800 |
3,040 |
NOTE: The student counts are based on an older NAEP frame and the measures of size are based on an assignment of schools to poverty status based on percent free or reduced lunch students from the NAEP frame. This table will be updated based on the current CCD and SAIPE data when the school frame is ready.
Within each of the four grade-span strata, three school-size strata will be generated (small, medium, and large). The cutoffs for enrollment counts will be the weighted terciles within each of the grade-span strata (weighted by student enrollment). For example, for elementary schools, the small-size stratum will consist of schools with enrollments below the 33rd weighted percentile of enrollment over all elementary schools on the frame.13 Thus the small-size stratum will represent 33 percent of all enrollment within elementary schools. Similarly, the medium-size stratum for elementary schools will consist of schools with enrollments between the 33rd and 67th weighted percentiles of elementary schools.
The balanced sampling procedure will consist of having three levels of stratification:
stratification by sampled districts (with set sample sizes for each sampled district);
stratification by grade-span and school performance status; and
stratification by grade-span and grade-size strata.
The
initial measure of size pij
for each school ij
(district i,
school j
within district i)
will be the school enrollment wij
divided by the district probability of selection
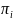 .
Suppose the stratification cells are subscripted by s=1,
2, 3 (1=districts; 2=school span and school performance status;
3=school span and school size), with stratification cells cs=1,…,Cs,
and assigned sample sizes nsc
(c=1,…,Cs,
s=1,
2, 3). The Deville-Tillé balanced sampling algorithm will be
used to draw the school sample with these initial measures of size
and meeting the three sets stratification cell sample sizes to the
extent possible.
.
Suppose the stratification cells are subscripted by s=1,
2, 3 (1=districts; 2=school span and school performance status;
3=school span and school size), with stratification cells cs=1,…,Cs,
and assigned sample sizes nsc
(c=1,…,Cs,
s=1,
2, 3). The Deville-Tillé balanced sampling algorithm will be
used to draw the school sample with these initial measures of size
and meeting the three sets stratification cell sample sizes to the
extent possible.
B2.2 Estimation Procedures
Please see Part A, Sec. A16 for a discussion of our estimation procedures, and see Part B, Sec. B3 for a discussion of our weighting procedures.
B2.3 Degree of Accuracy Needed
The description of the degree of accuracy needed, from our original package (see reference in B2.1), is inserted below.
Table 9A below presents power calculations for population percentages for the design for a comparison of districts in RTT states and districts in non RTT states, with sample sizes of 725 and 484 respectively. Under the null hypothesis, the two populations have the same population percentage, and the difference is zero. The difference of sample percentages is an unbiased estimator of the true difference in percentages.
The null standard errors for the difference of sample percentages are given in the table assuming simple random sampling within the strata and independent samples.14 The ‘cutoff for a 95 percent two-sided critical region’ is 1.96 times the null standard error of the difference: the value of the estimated difference for which we will reject the null hypothesis of no difference in the populations. For example, in the first scenario of Table 7A, the critical region for rejection of the null is an absolute value of the difference greater than 5.75 percent (e.g., sample percentages of 50 percent and 44.25 percent for each population would be on the boundary of the critical region). The alternative population percentages provide an alternative hypothesis for which there will be 80 percent power: i.e., there is an 80 percent probability under this alternative of rejecting the null hypothesis. For example, in the first scenario of Table 7A, if the population percentage for non RTT states is 50 percent and the population percentage for RTT states is 41.9 percent, then there is at least an 80 percent chance that the null hypothesis will be rejected (i.e., that the sample percentage difference between non RTT and RTT states will exceed 5.75 percent15). The probability of failing to reject the null hypothesis in this case is only 20 percent.
Table 9B presents similar calculations, but in this case for the high poverty districts alone (high poverty districts in RTT states versus high poverty districts in non RTT states).
Table 9A. Power calculations for RTT vs. non RTT comparison
|
Null Population Percentage |
Effective sample size non RTT |
Effective sample size RTT |
Null standard error of difference |
Cutoff for 95% two-sided critical region for difference |
Alternative population percentage for non RTT with 80% power |
Alternative population percentage for RTT with 80% power |
Scenario 1 |
50% |
725 |
484 |
2.93% |
5.75% |
50% |
41.9% |
Scenario 2 |
40% |
725 |
484 |
2.88% |
5.64% |
40% |
32.1% |
Scenario 3 |
30% |
725 |
484 |
2.69% |
5.27% |
30% |
22.6% |
Scenario 4 |
20% |
725 |
484 |
2.35% |
4.60% |
20% |
13.6% |
Scenario 5 |
10% |
725 |
484 |
1.76% |
3.45% |
10% |
5.3% |
Table 9B. Power calculations for RTT vs. non RTT comparison within the high poverty districts
|
Null Population Percentage |
Effective sample size non RTT |
Effective sample size RTT |
Null standard error of difference |
Cutoff for 95% two-sided critical region for difference |
Alternative population percentage for non RTT with 80% power |
Alternative population percentage for RTT with 80% power |
Scenario 1 |
50% |
546 |
375 |
3.35% |
6.57% |
50% |
40.7% |
Scenario 2 |
40% |
546 |
375 |
3.29% |
6.44% |
40% |
31.0% |
Scenario 3 |
30% |
546 |
375 |
3.07% |
6.02% |
30% |
21.6% |
Scenario 4 |
20% |
546 |
375 |
2.68% |
5.26% |
20% |
12.7% |
Scenario 5 |
10% |
546 |
375 |
2.01% |
3.94% |
10% |
4.7% |
B2.4 Unusual Problems Requiring Specialized Sampling Procedures
There are no unusual problems requiring specialized sampling procedures.
B2.5 Use of Periodic (less than annual) Data Collection to Reduce Burden
Annual surveys will be conducted over the two-year data collection period in order to assess change over time within the brief period that ARRA funds can be used.
B.3 Methods to Maximize Response Rates
To help ensure a high response rate, as the initial step, we will send letters to the sampled respondents (see Appendix D). The letters explain the nature and importance of the evaluation and provides the OMB clearance information, Westat contact information, the URL for the web survey and a username. We will send reminder emails or letters after 2 weeks and again after 4 weeks. Phone follow-up will be used for those individuals who do not respond after the second email reminder or letter. We will use a management database to track response rates and identify patterns of nonresponse.
Exhibit 2 summarizes the strategies we will undertake to maximize response rates. With these strategies being employed we expect an 80% response rate from schools, and 80% response rate from districts, and a 100% response rate from states.
Exhibit 2. Strategies to Maximize Response Rates
Advance notification of survey |
|
Provide clear instructions and user-friendly materials |
|
Offer technical assistance for survey respondents |
|
Monitor progress regularly |
|
Weighting the district and school samples
After completion of field collection in each year, we plan to weight the data to provide a nationally representative estimator. Replicate weights will be generated to provide consistent jackknife replicate variance estimators (statistical packages such as STATA and SAS Version 9.2 allow for easy computation of replicate variance estimates). The development of replicate weights will facilitate the computation of standard errors for the complex analyses necessary for this survey. The replicates will be based fundamentally on the first-phase district sample (so that each replicate is associated with one set of ‘dropped’ districts), but the school weights will need to be carefully calibrated to provide school-level replicate weights that correctly reflect the effects of the balanced sampling process (the replicate weights are recalibrated to add to the stratum totals). We anticipate nonresponse, which we will adjust for by utilizing information about the nonresponding districts and schools from the frame and other sources regarding funding and other important district and school characteristics. This information will be used to generate nonresponse cells with differential response rates. The nonresponse adjustments will be equal to the inverse of the weighted response rate. This will adjust for bias from nonresponse.
The state survey was pre-tested with nine or fewer state officials. The school district survey was pre-tested with nine or fewer district officials. The school survey was pre-tested with nine or fewer school officials.
B.5 Individuals Consulted on Statistical Aspects of Design
The statistical aspects of the design have been reviewed by staff at the Institute of Education Sciences. The individuals most closely involved in developing the statistical procedures include:
Marsha Silverberg, IES, 202-208-7178
Meredith Bachman, IES, Project Officer, 202-219-2014
Babette Gutmann, Westat, project director, 301-738-3626
Patty Troppe, Westat, deputy project director, 301-294-3924
Lou Rizzo, Westat, senior statistician, 301-294-4486
Juanita Lucas-McLean, director of data collection, 301-294-2866
Bruce Haslam, Policy Studies Associates, director of design, 202-939-5333
Michael Puma, Chesapeake Research Associates, director of analysis, 410-897-4968
Sharon Lohr, Arizona State University, member of Technical Working Group, 480-965-4440
Thomas Cook, Northwestern University, member of Technical Working Group, 847-491-3776
1 The degree to which the State Fiscal Stabilization Fund and bolstering of already established programs (e.g., IDEA) successfully saved and created new education jobs is of policy interest as well. However, (a) this topic has been examined in other forums and (b) at the time when this study is fielded, funds tied to job retention and creation are unlikely to still be available to states, districts, and schools.
2 In defining district eligibility, we follow the criteria from the National Assessment of Educational Progress (NAEP). The NAEP macros for excluding districts are applied also in the generation of the district frame here.
3 This cutoff is the mean percentage of 5 to 17 year olds in poverty across SAIPE school districts in 2008.
4 These are tentative assignments based on preliminary frame calculations. We may make limited modifications of these when we have data from the fully complete frame, if some of our expectations are found to be in need of modification.
5 The student counts for the three RTT strata are from the preliminary district frame derived from 2008-09 and 2009-10 CCD frames. The percentages for the high and low poverty stratum within each RTT stratum are taken from the 2008 SAIPE district file.
6
A weighted estimate for a district-level characteristic from a PPS
sample of districts (with weight equal to measure of size divided by
probability of selection) has a standard error essentially
equivalent to that of a simple random sample (see for example
Equation 9A.22 of Cochran 1977 (Cochran, W. G. (1977), Sampling
Techniques, 3rd ed., New York: John
Wiley & Sons)). Under simple random sampling, if
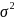 is the population variance, then the standard error is
is the population variance, then the standard error is
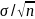 ,
and the normalized standard error is
,
and the normalized standard error is
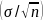 /
/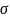 =
=
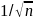 .
Note that this ignores the beneficial effects of stratification
within each of the three major strata: the standard errors in Table
1 are conservative (a slight overestimate).
.
Note that this ignores the beneficial effects of stratification
within each of the three major strata: the standard errors in Table
1 are conservative (a slight overestimate).
7 This sorts within each higher-level stratum as lowest to highest, highest to lowest, lowest to highest, etc. The intention is to spread the distribution across the sort as much as possible when a systematic sort is carried out.
8 One-school districts are districts with only one school. These will be undersampled by a factor of ¼: see the section on one-school districts below.
9 From American Fact Finder on the US Census website, the American Community Survey percentage of 5 to 17 year olds in poverty is 17.0 percent for 2008 and 18.7 percent in 2009. Aggregating poverty percentages over the 13,742 school districts on the 2008 SAIPE file gives a poverty rate of 16.7 percent. This poverty rate will be used as the cutoff for determining high vs. low poverty status. It should be noted that the weighted median over the SAIPE school districts is 15.2 percent, so that there will be more than 50 percent student population in the low-poverty districts (actually 56.8 percent, see Table 2).
10 What we will not do is carry out a rejective procedure of drawing samples and discarding them if they do not have the necessary characteristics. One and only one sample will be drawn, and it will be accepted. This will maintain the integrity of the sample design.
11 Deville, J.-C., and Tillé, Y. (2004). Efficient balanced sampling: The cube method. Biometrika 91, 4, 893-912.
12 What we will not do is a controlled selection approach where the sampling is not truly randomized. Our final sampling plan will meet the stratification requirements at least approximately while remaining fully randomized, with known inclusion probabilities for each school on the frame.
13 The school frame actually consists of the schools within the 1,700 sampled districts, which are then weighted by the inverse of the district probability of selection.
14 This is sqrt (P0*(1-P0)*((1/n1)+(1/n2))), where P0 is the null population percentage, n1 is the effective sample size in non RTT states, and n2 is the effective sample size in RTT states.
15 The standard error of the difference under the alternative hypothesis is sqrt ((P1*(1-P1)/n1)+ (P2*(1-P2)/n2)), where P1 is the non RTT population percentage, n1 is the sample size in non RTT states, P2 is the RTT population percentage, and n2 is the sample size in RTT states.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Title | Abt Double-Sided Body Template |
| Author | Abt Associates Inc |
| File Modified | 0000-00-00 |
| File Created | 2021-01-31 |
© 2025 OMB.report | Privacy Policy