Att_1850-0884 4718 SSBT06844-PartB
Att_1850-0884 4718 SSBT06844-PartB.docx
Impact Evaluation of Race to the Top (RTT) and School Improvement Grants (SIG)
OMB: 1850-0884
Impact
Evaluation of RTT
and SIG: OMB Data Collection Package
November 21, 2011




CONTENTS
PART B. SUPPORTING STATEMENT FOR PAPERWORK REDUCTION ACT SUBMISSION 1
B. Collection of Information Requiring Statistical Methods 1
1. Respondent Universe and Sampling Methods 1
2. Procedures for the Collection of Information 7
3. Methods to Maximize Response Rates and Deal with Nonresponse 17
4. Pilot Testing 18
5. Individuals Consulted on Statistical Aspects of the Design 18
REFERENCES 21
APPENDIX A: PROTOCOL FOR STATE INTERVIEWS
APPENDIX B: PROTOCOL FOR DISTRICT INTERVIEWS
APPENDIX C: SCHOOL SURVEY
APPENDIX D: DATA COLLECTION FORM FOR STATE-LEVEL DATA
REQUEST
APPENDIX E: DATA COLLECTION FORM FOR DISTRICT-LEVEL DATA
REQUEST
PART B. SUPPORTING STATEMENT FOR
PAPERWORK
REDUCTION ACT SUBMISSION
This Office of Management and Budget (OMB) package requests clearance for data collection activities to support the Impact Evaluation of Race to the Top (RTT) and School Improvement Grants (SIG). The RTT-SIG evaluation will provide important information on the implementation and impacts of school turnaround efforts and educational reforms funded through these two federal grant programs. The Institute of Education Sciences (IES) at the U.S. Department of Education (ED) has contracted with Mathematica Policy Research and its subcontractors, the American Institutes for Research (AIR) and Social Policy Research Associates (SPR), to conduct this important evaluation.
The RTT-SIG evaluation will include implementation and impact components. For the evaluation of RTT, the implementation component will include semistructured interviews with state officials, and an interrupted time series (ITS) design will be used to examine the relationship between RTT and student outcomes. For the evaluation of RTT- and SIG-funded school turnaround models (STMs), the implementation component will include semistructured interviews with state and district officials and a web survey of school administrators. The plan is for the impact evaluation of STMs to be based on a regression discontinuity design (RDD).
This is the second submission of a two-stage clearance request. The package was submitted in two stages because the study schedule required that recruitment efforts begin before all the study’s data collection instruments were developed. The first package (approved June 27, 2011, under OMB # 1850-0884) requested approval for recruitment of states, districts, and schools. This second package requests clearance to collect data that will support the full-scale study.
B. Collection of Information Requiring Statistical Methods
1. Respondent Universe and Sampling Methods
The investments being made by the U.S. Department of Education in Race to the Top and School Improvement Grants are unprecedented in scope and scale. To advance comprehensive and coherent education reforms across districts for the purpose of improving student outcomes, Congress appropriated $4 billion in American Recovery and Reinvestment Act of 2009 (ARRA) funding for the main RTT grant competition to encourage and reward states already implementing significant education reforms in four priority areas: (1) standards and assessments, (2) data systems, (3) effective teachers and school leaders, and (4) turning around persistently low-performing schools. RTT grants were awarded competitively in two phases. Phase I awards were announced in March 2010 to Tennessee ($500 million) and Delaware ($100 million). Phase II awards were made in August 2010 to New York ($700 million), Florida ($700 million), Georgia ($400 million), North Carolina ($400 million), Ohio ($400 million), Massachusetts ($250 million), Maryland ($250 million), Rhode Island ($75 million), Hawaii ($75 million), and the District of Columbia ($75 million).1
The SIG program was funded in fiscal year 2009 with $546.6 million, and received an additional $3 billion from ARRA (Pub. L. 111-5). SIG funds go to states based on their share of Title I funding; states then distribute the funds to districts with the lowest-achieving Title I schools that demonstrate need and a strong commitment to implement one of four models—turnaround, restart, closure, and transformation—aimed at improving or closing these persistently low-performing schools.
Given the scale and scope of these federal investments, findings from the RTT-SIG evaluation will be highly anticipated and critically scrutinized by a broad audience of policymakers, educators, and other interested parties. These constituents will want to know whether these programs accomplished their goals: Are struggling schools initiating reforms? Are states improving their data systems? Are common standards and assessments being adopted? Are teachers and principals being supported in their attempts to turn around lowest-achieving schools? In addition to these and other questions of program implementation, there is the bottom-line question of whether these reforms affect students’ academic achievement and progress beyond high school.
The RTT-SIG evaluation will examine the following research questions:
How are RTT and SIG implemented at the state, district, and school levels?
Are RTT reforms related to improvement in student outcomes?
Does receipt of RTT and/or SIG funding to implement a school turnaround model have an impact on outcomes for lowest-achieving schools?
Is implementation of the four school turnaround models, and strategies within those models, related to improvement in outcomes for lowest-achieving schools?
The RTT-SIG evaluation is designed to provide a descriptive account of the implementation of RTT and SIG, the most rigorous possible estimates of the effects of RTT and SIG, and the contextual information needed to fully understand and interpret those effects. The study will involve two samples, one for the evaluation of RTT and one for the evaluation of STMs (see Figure B.1 and description below).
Figure B.1. Diagram of Study Samples
The sample for the evaluation of RTT (the RTT sample) includes all 50 states and the District of Columbia. Interviews with representatives of the RTT grantee states will provide an understanding of the educational reforms they have implemented. We will be gathering the same information from non-RTT states so that we can understand the comparison condition and document the reforms that have been implemented in those states. This information will help with the interpretation of outcomes gains associated with RTT, which will contrast educational outcomes over time between the RTT-winning states and either the 12 RTT runner-up states with the next-highest application scores or all other non-RTT states.2
The sample for the evaluation of STMs (the STM sample) consists of about 1,200 schools from an estimated 134 school districts across 30 states (roughly 600 schools will form the treatment group, which represents about three quarters of all SIG grant recipients, and roughly 600 will form the comparison group).3 The treatment group will consist of schools in the first two of three eligibility tiers (Tiers 1 and 2) for SIG, while the comparison group will consist of schools either in the third eligibility tier (Tier 3) or ineligible.
The STM sample is purposefully selected to maximize the statistical precision of the RDD impacts. The states and districts that contribute the most to statistical precision are those where the number of treatment and comparison schools is largest and where the “fuzziness” of the RDD is lowest (meaning that a high proportion of schools in the treatment group actually receive STM funds and a low proportion in the comparison group receive them). Using estimates of fuzziness and sample size based on information gathered through a review of states’ SIG application materials and conversations with state administrative staff, we calculate the minimum detectable effect (MDE) corresponding to every opportunity to estimate an RDD impact in every state. We then rank those opportunities and prioritize recruiting the states and districts corresponding to the opportunities with lower MDE values.
To address the study’s research questions, the evaluation will collect and analyze data from five sources, which include interviews, a survey, and extant data. The interview protocols and survey were developed by the evaluation team and align with the four assurance areas of RTT (college- and career-ready standards and high-quality assessments, data systems that trace progress and foster continuous improvement, teacher and principal effectiveness, and turning around low-performing schools). Prior to developing the instruments, the evaluation team conducted a review of RTT and SIG applications to help ensure that the response categories used in the instruments reflect the types of reforms states plan to implement. The evaluation team also consulted with a Technical Working Group and ED to obtain information on priority topics for the evaluation’s data collection instruments. The proposed data collection has an anticipated response rate of 85 percent; the components of the data collection are described below.
State Interviews. We will conduct semistructured telephone interviews with representatives from the state education agency in every state and the District of Columbia (Appendix A). The interviews will consist of topic-specific modules that may be administered to different state-level respondents. States in the RTT sample that did not receive RTT grants will be asked about their implementation of RTT-related reforms. All states will be asked detailed questions about their policies and supports for school turnaround.
District Interviews. We will conduct semistructured telephone interviews with district-level administrators from each district in the STM impact study (about 134 districts) (Appendix B). These interviews will document school turnaround efforts and supports provided by the district to turnaround schools. Like the state interview, the district interview will consist of topic-specific modules that may be administered to different district-level respondents.
School Surveys. We will conduct a web survey of school administrators (principals, assistant principals, or other staff knowledgeable about school turnaround activities) at the approximately 1,200 schools that are part of the STM sample (Appendix C). To ease burden on respondents, we will limit the length of the survey to 45 minutes. Because the information we need to obtain from schools is considerable, items on the instrument capture specific areas of interest through closed-ended questions and offer specific and mutually exclusive response options.
Administrative Data on Student Outcomes. We will request standardized test scores on state proficiency assessments; high school graduation rates; and (to the extent data are available) college enrollment rates and completion of at least a year of college credit.4 In addition to test scores, we will request that the state (or district if necessary) provide data on student characteristics such as sex, race/ethnicity, birth year, grade, eligibility for free or reduced-price lunch, and English language learner status. Student-level data will be collected for the STM impact analysis only; the RTT outcomes analysis will rely on administrative data aggregated to the state, district, or school levels. We are assuming that we will be able to obtain the necessary student-level outcome data directly from state data systems for some states, but that we will need to obtain student-level data from districts in other states. We will develop two forms to collect outcomes data—one for states and one for districts—to show states (and districts, when necessary) the data we need (appendices D and E).5
National Assessment of Educational Progress (NAEP) Scores. We will obtain state-level NAEP scores from ED. The NAEP scores are available for grades 4 and 8, for both math and reading, every other year. In 2001, participation in state NAEP tests was made mandatory for states receiving Title I funds. Thus, we plan to use at least four years of data prior to RTT grants (2003, 2005, 2007, 2009) and two years of post-RTT data (2011 and 2013, which will become available in spring 2012 and spring 2014, respectively).
The RTT-SIG evaluation is expected to be completed in five years, with three years of data collection. Table B.1 shows the schedule of data collection activities.
Table B.1. Data Collection Timetable
Activity |
Date |
2011 |
|
Solidify Participation of Study Sample |
6/2011 through 1/2012 |
2012 |
|
Collect Interview Data |
3/2012 through 6/2012 |
Collect Survey Data |
3/2012 through 6/2012 |
Collect Administrative and NAEP Data |
7/2012 through 10/2012 |
2013 |
|
Collect Interview Data |
3/2013 through 6/2013 |
Collect Survey Data |
3/2013 through 6/2013 |
Collect Administrative Data |
7/2013 through 10/2013 |
2014 |
|
Collect Interview Data |
3/2014 through 6/2014 |
Collect Survey Data |
3/2014 through 6/2014 |
Collect Administrative and NAEP Data |
7/2014 through 10/2014 |
NAEP = National Assessment of Educational Progress.
Table B.2 lists the research questions and the data sources that will be used to answer them. We describe the study’s use of each data source in more detail below.
Table B.2. Research Questions and Data Sources
Research Question |
Data Source(s) |
1. How are RTT and SIG implemented at the state, district, and school levels? |
School surveys State and district interviews |
2. Are RTT reforms related to improvement in student outcomes? |
NAEP data Aggregated state extant data |
3. Does receipt of RTT and/or SIG funding to implement a school turnaround model have an impact on outcomes for lowest-achieving schools? |
State and district extant data |
4. Is implementation of the four school turnaround models, and strategies within those models, related to improvement in outcomes for lowest-achieving schools? |
State and district extant data School surveys State and district interviews |
NAEP = National Assessment of Educational Progress.
State Interviews. These interviews will focus on RTT policies and practices at the state level, as well as state policies and practices designed to support school turnaround through RTT and SIG. We will use this information primarily to examine research question 1, but perhaps also to examine whether impacts of STMs vary with respect to these implementation details (research question 4). States in the RTT sample that did not receive RTT grants will be asked about their implementation of RTT-related reforms.
District Interviews. Interviews with districts in the STM sample will focus on how state and district STM policies play out in districts and schools, including documenting the STM supports and information received by the districts from the states. We will use the information from the interviews with districts in the STM sample to examine the implementation of SIG (research question 1) and whether impacts of STMs vary with respect to these implementation details (research question 4).
School Surveys. These surveys will focus on implementation of STMs in schools and the STM-related supports, information, and policies rolled out by the state and district. We will use this information to examine SIG implementation (research question 1) and whether impacts of STMs vary with respect to these implementation details (research question 4).
State and District Extant Data. The outcomes for the outcomes analyses will come from student-level administrative data maintained by states and districts, as well as from the NAEP data the study team obtains from ED. (Student-level data will be collected for the STM impact analysis only; the RTT outcomes analysis will rely on administrative data aggregated to the state, district, or school levels.) The outcomes of interest for this study are student standardized test scores (state assessments and NAEP), high school graduation and attendance rates, and (to the extent data are available) college enrollment rates and completion of at least a year of college credit.
2. Procedures for the Collection of Information
a. Statistical Methodology for Stratification and Sample Selection
We will not draw a random sample of districts for the STM component. Rather, states, districts, and schools will be selected purposefully to provide information on implementation and to support a rigorous analysis of program impacts (see Figure B.1). All 50 states and the District of Columbia will be included in the sample for the evaluation of RTT. The sample for the evaluation of STMs will consist of about 1,200 schools from an estimated 134 school districts across 30 states (roughly 600 schools will form the treatment group and 600 the comparison group).6 The districts in the STM sample will be purposefully selected to maximize the statistical precision of the RDD impacts.
b. Estimation Procedures
Our estimation procedures include four sets of analyses aligned to the research questions.
Implementation Analysis. To thoroughly document the extent to which states, districts, and schools have implemented RTT and SIG systems and requirements, we will use data collected through interviews with state and district representatives and surveys of school administrators. We will use descriptive analyses to report observed patterns in the data. We will also describe implementation by key groups at different levels. For the RTT sample, we will report findings separately for RTT states and non-RTT states. For the STM sample at the district level, we will report what district representatives recount in response to questions about the treatment and comparison schools in their districts. For the STM sample at the school level, we will report findings separately for schools that received STM funding and for schools that did not. We will use the data to compare responses to questions about implementation from year to year. Implementation analyses will be used to help interpret the impacts of STM by describing the implementation of STMs in the treatment group and the reform experiences of schools in the comparison group.
Because we plan to estimate the impacts of STMs using an RDD (which generates impact estimates that apply primarily to schools at the cutoff value of an assignment variable), it will also be important to describe the difference in reform experiences between the treatment and comparison groups near the cutoff value of the RDD assignment variable. In calculating the difference in treatment and comparison group reform experiences at the cutoff value of the assignment variable, we will use the same analytic techniques for calculating outcome differences. The data source for these analyses will be the school administrator survey. In comparing the average experiences of the full treatment and comparison groups, we will draw on the school administrator survey and interviews with district representatives.
RTT Outcomes Analysis. We will use an ITS design to assess how student outcomes change following the receipt of RTT grants. The ITS design will take advantage of the timing of RTT grants. The ITS model projects the outcomes that would have been expected in the absence of RTT funding and compares the projections with the pattern of outcomes actually observed in the post-intervention period. The effect of the intervention is estimated as the difference between the predicted pattern of outcomes and the actual trend in outcomes in the post-intervention period.
To strengthen the validity of our estimates and to increase statistical power, our ITS design will also incorporate a comparison group of states that did not win RTT funding. This will be accomplished by using the estimated difference in outcomes between RTT winners and losers who were on the cusp of winning or losing RTT as the outcome in the ITS analysis. In forming this comparison group, we will take advantage of the application scores used to select RTT winners in the second phase of the competition. The cutoff value on this score is the lowest application score received by one of the 10 winning Phase II applicants.
The ITS approach is illustrated graphically in Figure B.2. Figure B.2 shows the estimated difference in NAEP scores between states that just won RTT in Phase II and states that just lost RTT in 2003, 2005, 2007, and 2009, with the cutoff year between receiving and not receiving RTT funds taken to be 2010. We focus on Phase II winners because Phase I winners lack a Phase II application score, which is needed to adjust for the application score when calculating the difference between RTT and non-RTT outcomes in each year. The solid line shows the (linear) trend in outcomes estimated on the basis of the period before the intervention, which is then extended to the post-intervention period (dashed line). The gains associated with RTT in the post-RTT years are estimated as the average deviation from this projected trend. Actual outcomes in the post-RTT years are shown by the squares in the figure.
Figure B.2. Illustration of the ITS Design
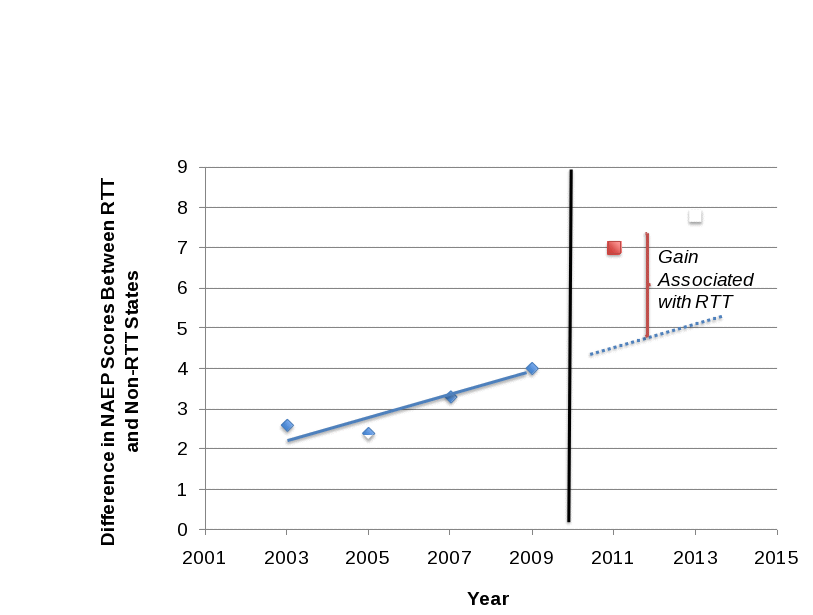
For our benchmark ITS analysis, we will use an approach consistent with Figure B.2. Specifically, we will estimate a linear trend using the difference in NAEP scores7 from 2003, 2005, 2007, and 2009 between the 10 Phase II RTT grantees and 12 non-RTT states in our sample. We will then analyze outcomes by examining the difference between that trend and the observed difference between those two groups of states in 2011 and 2013.
Estimation involves a two-step procedure. In the first step, we estimate the average difference in outcomes between states that just won RTT and states that just lost RTT in each year. We will estimate this difference using a simplified RDD approach8 in each year using equations 1 and 2.
(1)
![]()
(2)
![]()
Equations 1 and 2 will be estimated separately in each year. The
superscripts R and L denote the right (treatment) and
left (comparison) sides of the RDD cutoff value, Yi
is the outcome for state i, Xi
is the RTT application score centered at the cutoff value, Zi
is a set of mean-centered pre-RTT covariates, and εi
is the error term. The interpretation of the constant term in a
regression is the expected mean outcome when all covariates equal
zero. Thus, the assignment variable is centered at the RDD cutoff
value so that the intercept terms in equations 1 and 2 represent the
predicted value of the outcome variable at the cutoff value. Thus,
the RDD-adjusted difference in outcomes between RTT and non-RTT
states is estimated by the difference in intercept terms: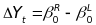 .
.
In the second
step,
 becomes the outcome in an ITS estimation equation:
becomes the outcome in an ITS estimation equation:
(3) 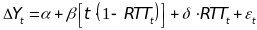
where
 is
the difference between RTT and non-RTT states in NAEP scores (in a
particular subject and grade) in year t. The term α
is a constant, β
is a linear trend, and RTTt is an indicator
of whether year t is after RTT funding begins. The time
variable, t, will be centered at 2010 (the year RTT grantees
began receiving their funding). This regression does not include
additional covariates due to a lack of available degrees of freedom.
Because
is
the difference between RTT and non-RTT states in NAEP scores (in a
particular subject and grade) in year t. The term α
is a constant, β
is a linear trend, and RTTt is an indicator
of whether year t is after RTT funding begins. The time
variable, t, will be centered at 2010 (the year RTT grantees
began receiving their funding). This regression does not include
additional covariates due to a lack of available degrees of freedom.
Because
 is an
estimate with potentially varying precision across years, we will
estimate equation 3 using inverse variance weights.
is an
estimate with potentially varying precision across years, we will
estimate equation 3 using inverse variance weights.
The outcome gains
associated with RTT are
![]() .
As discussed, the gains associated with RTT are the deviation
relative to the pre-existing trend. The reason we subtract
.
As discussed, the gains associated with RTT are the deviation
relative to the pre-existing trend. The reason we subtract
![]() is to account for the rise in the projected trend line over the two
years between 2010 and 2012 (2012 is the average of 2011 and 2013,
the two post-RTT data points whose average is estimated by
is to account for the rise in the projected trend line over the two
years between 2010 and 2012 (2012 is the average of 2011 and 2013,
the two post-RTT data points whose average is estimated by
![]() ).
We will also calculate outcome gains separately for 2011 and 2013 by
replacing the single RTT indicator with two, one for each post year
(for the study’s first report with outcome findings, only 2011
data will be available).
).
We will also calculate outcome gains separately for 2011 and 2013 by
replacing the single RTT indicator with two, one for each post year
(for the study’s first report with outcome findings, only 2011
data will be available).
STM Impact Analysis. Unless it is not feasible, we plan to use an RDD to estimate the impact of STM funding on student outcomes. The rules from ED about the prioritization of state STM funds to the persistently lowest-achieving schools create the opportunity for an RDD, generally considered one of the strongest quasi-experimental designs (see, for example, Shadish et al. 2002). Student-level data used for this analysis will come from two sources: (1) school districts recruited for the study, and (2) extant data from the data systems of states. The recruited school districts will include about 600 treatment and 600 comparison group schools.
The RDD component of this study can be characterized as a set of many mini-studies, each corresponding to a specific combination of state, outcome, and grade level. For some mini-studies, schools could be assigned using two assignment variables (average achievement and graduation rate), and we will estimate separate impacts for each assignment variable. We will conduct a separate RDD analysis for each mini-study, because the relationship between the outcome and the assignment variable could vary across mini-studies, and estimating that relationship accurately is essential for obtaining unbiased impacts.
For each mini-study, we plan to estimate intent-to-treat (ITT) impacts and the complier average causal effect (CACE). The ITT impact is the impact of being below the cutoff value on the assignment variable (the impact of being eligible for STM funding). Because not all schools below the cutoff value will actually receive STM funding (preliminary calculations reveal that about 70 percent of schools that would be in our treatment group received funding), the ITT impact does not correspond to the impact of being offered, or of receiving, STM funding. Both the impact of being offered STM funding (measured using SIG award information from state websites and reported in Hurlburt et al. 2011) and the impact of actually receiving STM funding (measured using the STM school survey) will be estimated using CACE analysis. Therefore the CACE impacts are likely to be of greatest policy impacts.
The ITT impact estimation equations for the mini-studies, in which the unit of assignment is the school, are:
(4)
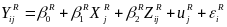 ,
,
(5)
 ,
,
where
the superscripts R and L denote the right and left
sides of the RDD cutoff value,
![]() is the outcome (for example, scores on the state assessment or
postsecondary matriculation) for student i in school j,
is the outcome (for example, scores on the state assessment or
postsecondary matriculation) for student i in school j,
![]() is the assignment variable centered at the cutoff value (either
school-level achievement or graduation rate, depending on which
assignment variable is used in a particular mini-study),
is the assignment variable centered at the cutoff value (either
school-level achievement or graduation rate, depending on which
assignment variable is used in a particular mini-study),
![]() is a set of mean-centered baseline covariates,
is a set of mean-centered baseline covariates,
![]() is a school-level error term, and
is a school-level error term, and
![]() is a student-level error term. The interpretation of the constant
term in a regression is the expected mean outcome when all covariates
equal zero. Thus, the assignment variable is centered at the RDD
cutoff value so that the intercept terms in equations 4 and 5
represent the predicted value of the outcome variable at the cutoff
value. Similarly, the covariates
is a student-level error term. The interpretation of the constant
term in a regression is the expected mean outcome when all covariates
equal zero. Thus, the assignment variable is centered at the RDD
cutoff value so that the intercept terms in equations 4 and 5
represent the predicted value of the outcome variable at the cutoff
value. Similarly, the covariates
![]() are mean-centered. The RDD impact of STM funding receipt on the
outcome is estimated by the difference in intercept terms:
are mean-centered. The RDD impact of STM funding receipt on the
outcome is estimated by the difference in intercept terms:
![]() .
The baseline covariates
.
The baseline covariates
![]() are included in this model to increase precision and will vary by
state and district depending on data availability.
are included in this model to increase precision and will vary by
state and district depending on data availability.
An RDD in which the difference in the intervention participation rate between the treatment and comparison groups is less than 100 percent is known as a “fuzzy” RDD (Trochim 1984; Hahn et al. 2001). In the context of a fuzzy RDD, it is possible to estimate the impact either of receiving an offer of STM funding or of actually receiving STM funding by calculating the CACE. To calculate CACE impacts, we will add two estimating equations:
(6)
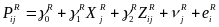 ,
,
(7)
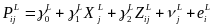 ,
,
where
P is an indicator of whether a school is offered (or receives)
STM funding, and other variables are defined similarly to equations
(4) and (5). The impact on being offered (or receiving) STM funding
is
![]() , and the CACE impact is
, and the CACE impact is
![]() .
.
If it is not feasible to implement an RDD, we will use an ITS design to assess how student outcomes change following the implementation of an STM. The ITS design will take advantage of the timing of STM implementation. The ITS model projects the outcomes that would have been expected in the absence of the STM and compares the projections with the pattern of outcomes actually observed in the post-intervention period. The effect of STM implementation is estimated as the difference between the predicted pattern of outcomes and the actual outcomes observed in the post-intervention period. To strengthen the validity of our estimates and to increase statistical power, our ITS design will also incorporate a comparison group of schools that did not receive STM funding. This will be accomplished by using the difference in outcomes between schools that do and do not receive STM funding as the outcome in the ITS analysis. The sample of schools used to estimate impacts with this ITS design would be based on the sample identified for estimating RDD impacts, but augmented to reduce any observed differences between our analysis sample and the national population of SIG grantees.
Relating Student Outcome Gains to STMs and Practices. We will use an ITS design to assess how student outcomes change following the implementation of an STM. The ITS design will take advantage of the timing of STM implementation. The ITS model projects the outcomes that would have been expected in the absence of the STM or practice and compares the projections with the pattern of outcomes actually observed in the post-intervention period. The effect of the STM or practice is estimated as the difference between the predicted pattern of outcomes and the actual outcomes observed in the post-intervention period.
After outcome gains have been estimated for every school in our sample that implemented an STM, we will examine the relationship between those gains and the specific STM and individual practices that each school implemented.
When interpreting findings we will clarify that variation in outcome gains across STMs and practices could be due to unobserved characteristics of schools and cannot necessarily be attributed to the models or practices themselves. This is because the mechanism used to assign STMs and associated practices to schools is unknown, meaning that we cannot adjust for it
Our approach to estimating the relationship between improvements in student outcomes and specific models or practices involves four steps. First, we will assess which STMs and practices can be analyzed with the available data, creating “bundles” of practices when practices cannot be analyzed individually. Second, we will estimate outcome gains for every grade in each school in our sample that implemented an STM. Third, we will examine the relationship between the estimated school-specific gains and the specific STM and practices implemented in schools. Fourth, we will aggregate these relationships across grades.
The ITS model is
shown in equation (8), where: Y is the outcome (in the case of
test scores, Y is transformed into a z-score9);
t is the year (centered at the 2010–2011 school year);
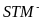 is a
binary variable that equals 1 for years prior to 2010–2011 and
0 otherwise;
is a
binary variable that equals 1 for years prior to 2010–2011 and
0 otherwise;
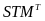 (T
corresponds to outcome year 1, 2, or 3) is a binary variable that
equals 1 when t = T and 0 otherwise;
(T
corresponds to outcome year 1, 2, or 3) is a binary variable that
equals 1 when t = T and 0 otherwise;
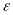 is an
error term; and
is an
error term; and
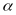 ,
,
 ,
,
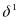 ,
,
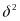 , and
, and
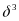 are
parameters to be estimated.
are
parameters to be estimated.
(8)
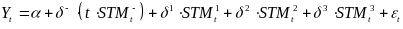
For an outcome year T, the outcome gain associated with STM
implementation for a given grade in a given school is
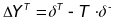 ,
which is the distance between the outcome in year T and the
trendline projected by the ITS model from the preintervention time
period.
,
which is the distance between the outcome in year T and the
trendline projected by the ITS model from the preintervention time
period.
To assess the
relationship between outcome gains and whether schools implement
specific models, we will estimate equation (9) separately for each
grade and outcome year (T) of interest, where: i
indexes schools;
 is
the outcome gain for a given grade of interest; STM is a set
of binary variables indicating which STM a school implemented; X
is a set of school characteristics that includes demographic
characteristics of the student body and the RDD assignment variables;
STATE is a set of binary variables indicating the state where
the school is located;
is
the outcome gain for a given grade of interest; STM is a set
of binary variables indicating which STM a school implemented; X
is a set of school characteristics that includes demographic
characteristics of the student body and the RDD assignment variables;
STATE is a set of binary variables indicating the state where
the school is located;
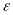 is an
error term; and
is an
error term; and
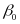 ,
,
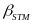 ,
,
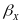 , and
, and
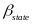 are
parameters to be estimated.
are
parameters to be estimated.
(9)
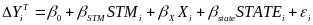
The differences
in outcome gains between STMs are given by the
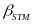 estimates. Because we include state indicator variables, these
estimates are based only on within-state variation, meaning that the
effects of STMs are not confounded with cross-state differences.
Also, because we are focusing on differences among STMs in outcome
gains, our estimates will be unaffected by changes over time that
affect all schools within a state (for example, changing state
assessments).
estimates. Because we include state indicator variables, these
estimates are based only on within-state variation, meaning that the
effects of STMs are not confounded with cross-state differences.
Also, because we are focusing on differences among STMs in outcome
gains, our estimates will be unaffected by changes over time that
affect all schools within a state (for example, changing state
assessments).
To estimate the
relationship between individual practices (or bundles of practices)
and outcome gains, we will estimate equation (10), which adds to
equation (9) the term
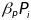 ,
where P is a set of binary variables indicating which
practices (or bundles of practices) were implemented in each school
and
,
where P is a set of binary variables indicating which
practices (or bundles of practices) were implemented in each school
and
 is a
set of parameters representing the differences in outcome gains
associated with those practices. Schools that implemented the closure
model will not be included in this analysis, since the closure model
cannot involve any other practices.
is a
set of parameters representing the differences in outcome gains
associated with those practices. Schools that implemented the closure
model will not be included in this analysis, since the closure model
cannot involve any other practices.
(10)
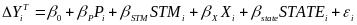
c. Degree of Accuracy Needed
i. RTT Outcomes
An ITS design will be used to examine the relationship between RTT and student outcomes. The study’s benchmark design calculates the impact of RTT as the change over time in the difference in NAEP scores between RTT states and a comparison group of non-RTT states, where the difference is calculated as an RDD impact (using states’ Phase II RTT application scores as the assignment variable).
Table B.3 shows the minimum detectable impacts (MDIs) and MDE sizes for the benchmark design and two alternative designs. The first alternative design is an ITS that does not include a comparison group of states. The second alternative design includes a comparison group, but calculates the difference between RTT and non-RTT states as a simple difference in means. These two alternatives are included to illustrate the precision benefits of including a comparison group in the ITS analysis and to illustrate the precision tradeoff between the benchmark design and a design that uses simple differences between RTT and non-RTT states instead of differences calculated as RDD impacts. The benchmark design should be less biased since it adjusts for the RTT application scores, but it does sacrifice some statistical precision.
The MDI for the benchmark design is 4.5 NAEP points, which is an effect size of 0.15 student-level standard deviations. Comparing the benchmark to Alternative 1, which has an MDI of 21.5 and an MDE of 0.7, we can see the precision benefit of including a comparison group. The precision tradeoff associated with using the benchmark approach (based on differences estimated using RDD impacts), instead of a simple difference in averages, is illustrated by Alternative 2, which has an MDI of 3.9 and an MDE of 0.13.
These calculations depend on assumptions based on analyses of 2009 fourth grade NAEP math scores for all students in a subset of 24 states in the RTT outcome analysis. Specifically, we assume that the average and standard deviations of NAEP scores are 240 and 29, respectively. We also calculated the variability across time in (1) mean RTT state NAEP scores, (2) mean differences between RTT and non-RTT states, and (3) differences between RTT and non-RTT states calculated as an RDD impact using the RTT application score as an assignment variable
Table B.3. RTT Minimum Detectable Impacts and Effect Sizes, NAEP 4th Grade Math Scores
|
ITS Design Options |
|||
|
Benchmark |
Alternative 1 |
Alternative 2 |
|
Treatment Sample |
10 Phase II RTT states |
All 12 RTT states |
All 12 RTT states |
|
Comparison Sample |
12 runner-up states |
None |
12 runner-up states |
|
Method to Calculate Treatment- Comparison Difference |
RDD impact using application score |
None |
Difference in means |
|
Pre-RTT Years |
4 |
4 |
4 |
|
Post-RTT Years |
2 |
2 |
2 |
|
MDIa |
4.5 |
21.5 |
3.9 |
|
MDEb |
0.15 |
0.74 |
0.13 |
|
Source: NAEP score for RTT sample states downloaded from [nces.ed.gov/nationsreportcard/naepdata].
Notes: The
MDI and MDE were calculated assuming (1) a two-tailed test, (2) a 5
percent significance level
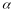 , (3)
an 80 percent level of power
, (3)
an 80 percent level of power
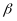 , (4)
no reduction in variance due to the use of regression models to
estimate impacts (limited degrees of freedom preclude additional
covariates), and (5) an assignment variable that follows the uniform
distribution. The table entries were calculated using the formula
, (4)
no reduction in variance due to the use of regression models to
estimate impacts (limited degrees of freedom preclude additional
covariates), and (5) an assignment variable that follows the uniform
distribution. The table entries were calculated using the formula
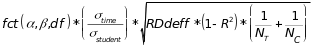 ,
where fct is the sum of two critical values (corresponding to
,
where fct is the sum of two critical values (corresponding to
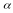 and
and
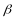 ) from
the T-distribution with df degrees of freedom; RDdeff
is the RDD effect corresponding to the uniform distribution (Schochet
2008), which also applies to the ITS design; time
is the estimated standard deviation of the state-level outcome
(either the mean NAEP score, the difference in simple mean NAEP
scores between RTT and non-RTT states, or the difference calculated
as an RDD impact) across time; student
is the student-level standard deviation in NAEP scores, and NT
and NC are the number units in the treatment
and control groups. To calculate the MDI, student
was set equal to 1.
) from
the T-distribution with df degrees of freedom; RDdeff
is the RDD effect corresponding to the uniform distribution (Schochet
2008), which also applies to the ITS design; time
is the estimated standard deviation of the state-level outcome
(either the mean NAEP score, the difference in simple mean NAEP
scores between RTT and non-RTT states, or the difference calculated
as an RDD impact) across time; student
is the student-level standard deviation in NAEP scores, and NT
and NC are the number units in the treatment
and control groups. To calculate the MDI, student
was set equal to 1.
a Minimum detectable impact, reported in NAEP scale units.
b Minimum detectable effect size, reported in effect size units, using the national student-level standard deviation.
ii. STM Impacts
Detecting an impact of STM on test scores close to 0.10 standard deviations (as requested by IES) using an RDD should be possible with a sample of 1,200 schools (600 in the treatment and 600 in the comparison group). In calculating the MDE for an RDD impact, one must account for (1) the correlation between the assignment variable and treatment variable, (2) clustering of students within schools, (3) fuzziness in the RDD, and (4) the sample size reduction that results from selecting an optimal bandwidth for estimating RDD impacts.
Table B.4 shows sample size requirements for the study for different assumptions regarding key design parameters. In a preliminary review of state SIG applications and awards to assess potential fuzziness, we found that a sample size of about 1,200 schools may be attainable within states that meet a maximum fuzziness requirement. Specifically, we measured the difference in the proportion of schools receiving awards between the treatment group (Tier I and II eligible schools) and the comparison group (Tier III eligible schools and noneligible schools). High differences in this proportion correspond to low levels of fuzziness. We assume that the proportion of schools receiving funds to implement an STM is zero in the study's comparison group, which is consistent with information we have received from states pertaining to the schools that are likely to be included in the study's comparison group. Based on an analysis of the relationship between fuzziness and finite sample bias, we found that the lowest value of the difference in this proportion that is acceptable for this study is 40 percent. In states where the difference is at least 40 percent, the average difference in the proportion of schools receiving awards between the treatment and comparison groups is 73 percent (termed a moderate degree of RD fuzziness in Table B.4. Also, from the evaluation of supplemental educational services, which also used an RDD, we found that the bandwidth typically excluded about half the analysis sample.
Table B.4. Differences in Proportions Between Treatment and Comparison Groups
Proportion of Schools Included in RDD Bandwidth |
Proportion of Treatment Group Implementing STM (Fuzziness) |
||
100 |
80 |
70 |
|
Number of Schools Needed for an MDE of 0.10 |
|||
100 percent |
400 |
625 |
825 |
75 percent |
550 |
850 |
1,100 |
50 percent |
800 |
1,250 |
1,650 |
Number of Schools Needed for an MDE of 0.15 |
|||
100 percent |
185 |
285 |
370 |
75 percent |
245 |
375 |
500 |
50 percent |
360 |
575 |
750 |
Note: The
numbers in the table represent the number of schools needed to
achieve the MDE targets specified in the shaded cells. The MDEs are
expressed in effect size units and were calculated assuming (1) a
two-tailed test, (2) a 5 percent significance level
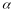 , (3)
an 80 percent level of power
, (3)
an 80 percent level of power
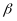 , (4)
a reduction in variance of 40 percent at the student level
, (4)
a reduction in variance of 40 percent at the student level
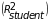 and
70 percent at the school level
and
70 percent at the school level
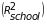 due
to the use of regression models to estimate impacts, (5) an
intra-class correlation of 0.15
due
to the use of regression models to estimate impacts, (5) an
intra-class correlation of 0.15
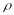 , and
(6) an RD assignment variable that follows the normal distribution.
The table entries were calculated using the following formula:
, and
(6) an RD assignment variable that follows the normal distribution.
The table entries were calculated using the following formula:
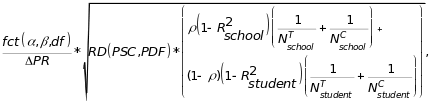
where fct
is the sum of two critical values (corresponding to
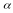 and
and
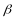 ) from
the T-distribution with df degrees of freedom; RD is
the regression discontinuity design effect (Schochet 2008);
) from
the T-distribution with df degrees of freedom; RD is
the regression discontinuity design effect (Schochet 2008);
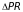 is
the difference in participation rates between students below and
above the RD cutoff (the degree of fuzziness in the design);
PSC is the proportion of students in the control group
(assumed to be 50 percent); PDF is the probability density
function of the assignment variable used to determine participation
in the RD design (assumed normal); and
is
the difference in participation rates between students below and
above the RD cutoff (the degree of fuzziness in the design);
PSC is the proportion of students in the control group
(assumed to be 50 percent); PDF is the probability density
function of the assignment variable used to determine participation
in the RD design (assumed normal); and
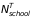 ,
,
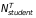 ,
,
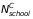 ,
,
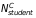 are
the number of schools and students in the treatment and control
groups (we assume 200 students per school). We assume no schools in
the comparison group implement STMs.
are
the number of schools and students in the treatment and control
groups (we assume 200 students per school). We assume no schools in
the comparison group implement STMs.
3. Methods to Maximize Response Rates and Deal with Nonresponse
States and districts receiving SIG and RTT grants are expected to report data on program performance and to participate in evaluations for the Secretary of Education, as explicitly stated in the RTT and SIG grant application forms (see page 19 of the SIG application [www2.ed.gov/programs/sif/application.doc] and pages 5, 14, and 96 of the RTT application [www2.ed.gov/programs/racetothetop/phase2-application.doc]). Despite this, some states and districts may face challenges in complying with the data request (e.g., due to staffing shortages) so we will work with states and districts to explain the importance of this data collection effort and to make it as easy as possible to comply.
A clear description of the study design presented to states and school districts, and the data collection’s reliance to a large degree on administrative data without any direct data collection from students or intrusion on classroom instructional time, will further encourage cooperation with evaluation efforts. Reducing districts’ burden in the submission of study data will facilitate attaining a high response rate on the administrative data collection. Federal rules permit ED and its designated agents to collect student demographic and existing achievement data from schools and districts without prior parental or student consent (Family Educational and Rights and Privacy Act (20 U.S.C. 1232g; 34 CFR Part 99)). To maximize the response rate and minimize burden on schools, we will follow these federal rules.
For the interviews with state and district administrators and the school administrator survey, we will be courteous but persistent in follow-up with participants who do not respond in a timely manner to our attempts to reach them.
We envision a multifaceted approach to reducing nonresponse on the school administrator survey. To ensure the targeted overall response rate of 85 percent, and to reduce the disparity in response rates between the treatment and comparison group samples, we will make the survey available in multiple modes so that sample members can complete it in the mode that is most convenient for them. We will alert them to the survey through an email message and/or a mailed letter, which will include their personalized login and password information. A second follow-up attempt will be made by sending a hard copy of the survey to administrators who do not respond within two to three weeks of the initial contact. Next, nonrespondents will be given the option of providing data over the telephone. We will use a hard copy form that is identical to the web questionnaire to minimize mode effects. For this effort, experienced interviewers will be recruited and extensively trained on data collection procedures, including methods for promoting cooperation among school administrators.
We are also proposing burden payments for the school administrator survey to partially offset respondents’ time and effort in completing the survey. During each round of data collection, we propose to offer $30 to administrators from comparison-group schools who complete the questionnaire in acknowledgement of the 45 minutes required. The amount is in keeping with the March 22, 2005 memo, “Guidelines for Incentives for NCEE Evaluation Studies,” prepared for OMB. This payment is proposed because high response rates are needed to make the survey findings reliable, and we are aware that school administrators are the targets of numerous requests to complete surveys on a wide variety of topics from state and district offices, independent researchers, and ED.
We will thoroughly test the web-based instrument for such features as clarity, accuracy, length, flow, and wording. To reduce item nonresponse, the web-based and CATI questionnaires will not allow respondents to enter out-of-range or inconsistent responses.
4. Pilot Testing
We will conduct pilot testing on the RTT-SIG school survey by administering it to nine administrators not included in the RTT-SIG sample. We will conduct a debriefing with each pilot test respondent to collect additional information about the questionnaire from the respondents’ perspective. We will conduct the pilot tests of the surveys in sets of three interviews so that any changes required can be included in the questionnaire for the remaining interviews. The district and state interviews will also be pilot tested prior to data collection. For the state interview, we will recruit and interview one or more staff members from one state receiving RTT and SIG funds and one state receiving SIG funds in order to ensure that the questions are clear for states in each group. For the district interview, we will select one district from a state receiving RTT funds that has at least one school implementing an STM.
5. Individuals Consulted on Statistical Aspects of the Design
The following study team and Technical Working Group members were consulted on various aspects of the statistical design:
Name |
Title and Affiliation |
Susanne James-Burdumy |
Associate Director of Research, Mathematica |
John Deke |
Senior Researcher, Mathematica |
Irma Perez-Johnson |
Senior Researcher, Mathematica |
Lisa Dragoset |
Researcher, Mathematica |
Thomas Fisher |
Fisher Education Consulting |
Brian Jacob |
Walter H. Annenberg Professor of Education Policy and Director of the Center on Local, State and Urban Policy at the Gerald R. Ford School of Public Policy, University of Michigan |
Elizabeth Stuart |
Assistant Professor in the Department of Mental Health and the Department of Biostatistics, Johns Hopkins University |
Guido Imbens |
Professor of Economics, Harvard University |
Thomas Cook |
Joan and Sarepta Harrison Chair in Ethics and Justice Professor of Sociology, Psychology, Education and Social Policy; Faculty Fellow, Institute for Policy Research, Northwestern University |
James Spillane |
Spencer T. and Ann W. Olin Chair in Learning and Organizational Change and Professor, School of Education and Social Policy, Northwestern University |
Jonathan Supovitz |
Associate
Professor and Director, Consortium |
Sean Reardon |
Associate Professor, Stanford University |
Thomas Kane |
Professor of Education and Economics, Harvard University |
Eric Smith |
Former Commissioner of Education, State of Florida |
The following people will be responsible for data collection and analysis:
Name |
Title and Affiliation |
Telephone |
Susanne James-Burdumy |
Associate Director of Research, Mathematica |
609-275-2248 |
John Deke |
Senior Researcher, Mathematica |
609-275-2230 |
Rebecca Herman |
Managing Research Analyst, AIR |
202-403-5449 |
Irma Perez-Johnson |
Senior Researcher, Mathematica |
609-275-2339 |
David DesRoches |
Senior Survey Researcher, Mathematica |
609-275-2366 |
Hahn, J., P. Todd, and W. Van Der Klaauw. “Regression Discontinuity.” Econometrica, vol. 69, no. 1, 2001, pp. 201-209.
Hurlburt, S., K. C. Le Floch, S. B. Therriault, and S. Cole. “Baseline Analyses of SIG Applications and SIG-Eligible and SIG-Awarded Schools.” (NCEE 2011-4019.) Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education, 2011.
Schochet, Peter Z. “Technical Methods Report: Guidelines for Multiple Testing in Impact Evaluations.” NCEE 2008-4018. Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education, 2008.
Shadish, W.R., T.D. Cook, and D.T. Campbell. Experimental and Quasi-experimental Designs for Generalized Causal Inference. Boston, MA: Houghton Mifflin, 2002.
Trochim, W.M.K. Research Design for Program Evaluation. Beverly Hills, CA: Sage Publications, 1984.
www.mathematica-mpr.com
Improving
public well-being by conducting high-quality, objective research and
surveys
Princeton,
NJ ■
Ann Arbor, MI ■
Cambridge, MA ■
Chicago, IL ■
Oakland, CA ■
Washington, DC
Mathematica®
is a registered trademark of Mathematica Policy Research

1 A third round of RTT grants will be awarded using funds appropriated in 2011. The fiscal year 2011 appropriation act also authorizes the Secretary to use RTT funds for grants to States for improving early childhood care and education.
2 ED recently announced that the nine states that were closest to winning RTT Phase 2 grants are eligible to compete for $200 million in additional funds. To compete, states will propose specific parts of their Phase 2 plans that they would implement with the new funds. While the new funding might have implications for interpretation and analysis, we do not currently see a need to change the study’s design or sampling plans. When we know which states win these additional funds and exactly what they intend to use them for, we will reassess our design and analysis plans.
3 Because of ED’s interest in the effects of the “restart” school turnaround model, the STM sample will also include the approximately 30 schools implementing that model.
4 To the extent possible, we will rely on EDFacts data, but the study’s data requirements will likely necessitate collecting data directly from states.
5 In states that are included only in the RTT sample, we will only request aggregate data at the school level on the outcomes of interest. We will develop an alternative data collection form for these states.
6 Because of ED’s interest in the effects of the “restart” school turnaround model, the STM sample will also include the approximately 30 schools implementing that model.
7 We frame this discussion in terms of NAEP scores but the same methods will be used for other outcomes.
8 Due to the relatively small number of states involved in this estimation and the potential for subjectivity in scoring RTT applications, this RDD approach will not have the same level of rigor as that used to estimate impacts of STMs. For example, we do not anticipate that findings based on this RDD analysis would meet WWC standards. However, even a simplified RDD approach will provide a more valid comparison than an approach that compares the average RTT state to the average non-RTT state, since the RDD approach does at least adjust for the RTT application score.
9 An individual student’s test score is converted into a z-score by subtracting from the student’s score the statewide mean score and then dividing by the statewide standard deviation.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | Kristin Hallgren |
| File Modified | 0000-00-00 |
| File Created | 2021-01-31 |
© 2025 OMB.report | Privacy Policy
