Att_1850-0877 4413 ARRA Evaluation Part B for baseline survey 4_1

This package is the second of three for the Integrated Evaluation of ARRA Funding, Implementation, and Outcomes. Our initial request (approved January 13^th, 2011 (see 1850-0877 v.1 (4385)) sought approval for execution of a sampling plan and recruitment of the selected sites. This package requests approval for an initial round of data collection that will include surveys of all states and a nationally representative sample of districts and schools in spring 2011. The third and final package will request approval for follow up surveys with the same groups in 2012 and 2013. A fast response from OMB is critical if the study is to field the spring 2011 surveys successfully, since much preparation work is necessary to ensure a high response rate from sampled school districts and schools.

Introduction

On February 17, 2009, President Obama signed the American Recovery and Reinvestment Act (ARRA) into law (Pub. L. 111-5). ARRA provides an unprecedented $100 billion of additional funding for the U.S. Department of Education (ED) to administer. While the initial goal of this money is to deliver emergency education funding to states, ARRA is also being used as an opportunity to spur innovation and reform at different levels of the U.S. educational system. Specifically, ARRA requires those receiving grant funds to commit to four core reforms: (1) adopting rigorous college-ready and career ready standards and high quality assessments, (2) establishing data systems and using data to improve performance, (3) increasing teacher effectiveness and the equitable distribution of effective teachers, and (4) turning around the lowest performing schools. Investment in these innovative strategies is intended to lead to improved results for students, long-term gains in school and local education agency (LEA) capacity for success, and increased productivity and effectiveness.

The education component of ARRA consists of several grant programs targeting states and LEAs and, in some cases, consortia led by non-profit organizations. The programs under ARRA fall into three general categories: (1) existing programs that received an infusion of funds (e.g., Individuals with Disabilities Education Act, Parts B & C; Title I; State Educational Technology grants; Statewide Longitudinal Data Systems grants); (2) a new program intended mainly for economic stabilization (i.e., State Fiscal Stabilization Fund); and (3) newly created programs that are reform-oriented in nature. Due to the number and scope of these programs, a large proportion of districts and schools across the country will get some ARRA funding. In turn, ARRA represents a unique opportunity to encourage the adoption of school improvement focused reforms and to learn from reform initiatives as they take place.

Although ARRA funds are being disbursed through different grant programs, their goals and strategies are complementary if not overlapping, as are the likely recipients of the funds. For this reason, an evaluative approach where data collection and analysis occurs across grant programs (i.e., it is “integrated”), rather than separately for each set of grantees will not only reduce respondent burden but will also provide critical information about the effect of ARRA as a whole.

Overview of the Study

The Integrated Evaluation of ARRA Funding, Implementation and Outcomes is being conducted under the Institute of Education Sciences (IES), ED’s independent research and evaluation arm. The study is one of several that IES will carry out to examine ARRA’s effects on education (see Exhibit 1).

Exhibit 1. IES Evaluation of ARRA’s Effects on Education

The Integrated Evaluation is designed to assess how ARRA efforts are unfolding over time and is therefore primarily descriptive. While information will be gathered on many of the grant programs, the evaluation will focus primarily on the reform-oriented programs (e.g., Race to the Top (RTT), Title I School Improvement Grants (SIG), Investing in Innovation (i3), and the Teacher Incentive Fund (TIF)) since those are of the greatest policy interest.¹ The study will support the various impact evaluations IES is conducting by providing critical context for those strategies being rigorously investigated – e.g., by documenting the relative frequency with which they are being implemented across the country, whether they are unique to the particular grant programs, and how they are being combined with other reform approaches.

To achieve these objectives, the Integrated Evaluation will draw heavily on existing information (grant funding allocations, district and school outcomes databases, performance reporting where available) and administer new surveys to all 50 states and to a nationally representative survey of districts and schools. The surveys will be conducted annually for at least three years, in spring 2011, 2012, and 2013.² In addition, two quick polls of a subsample of sampled districts will be conducted between the 2011 and 2012 and between the 2012 and 2013 larger surveys to capture key, evolving issues of interest to ED officials and other policy makers as they consider shifting technical assistance efforts and further legislative action.

B.1 Respondent Universe and Sampling Methods

We will administer surveys to states, school districts, and schools. The assembly of a universe frame and sampling plan for each is described below.

State Surveys

We will survey all 50 states and the District of Columbia; there is no sampling proposed for the state survey.

School District Surveys

We will construct a respondent pool and implement a sampling approach for each of the following:

A nationally representative sample of districts, with oversampling of certain ARRA program grantees, in order to track funding and implementation progress at this organizational level; and

A small nationally representative subsample of the nationally representative district sample, in order to obtain information on pressing policy and implementation concerns that might help ED refine technical assistance and legislative plans.

Nationally representative sample of school districts

We will draw a nationally representative sample of districts because ARRA is intended to stimulate broad system change and because, looking across all the ARRA programs, the expected recipients of funds are likely to include most districts. We anticipate that the amount and degree of ARRA funding will vary considerably, but most districts will receive at least some funding. A nationally representative sample then should provide a district sample with a range of funding levels. This sample will be augmented with a sample of districts that are grantees or subgrantees from two of the competitive ARRA programs – Race to the Top (RTT) and the Teacher Incentive Fund cohort 3 (TIF3) – because there is considerable policy interest in the types of reforms being undertaken in school districts that receive RTT and TIF funds in comparison to school districts that do not receive these funds, which are focused on the assurances of educator effectiveness and turning around low performing schools.

We will draw a probability proportionate to size (PPS) sample of districts, with number of students as the measure of size. This PPS sample design will be most efficient for district level estimators which are weighted by number of students. Using PPS designs is the most common and cost effective approach for selecting nationally representative samples.

To construct the sampling frame, we will use data from multiple sources, including (1) the National Center for Education Statistics’ Common Core of Data (CCD) for the universe of school districts, number of students, urbanicity, and poverty status; and (2) lists from ED on the TIF3 grantees.

We will draw a sample of 1,700 school districts out of 16,398 school districts.

Nationally representative subsample of school districts for polls

For each of the two polls, we will draw a random subsample of one quarter of the nationally representative sample of school districts, resulting in 400-450 districts in each subsample. School districts selected to receive the first poll will not be included in the sample to receive the second poll so that no district is unduly burdened by two polls.

School Surveys

We will construct a respondent pool and implement a sampling approach for:

A nationally representative sample of schools, with oversampling of schools likely to be affected by ARRA programs, in order to track funding and implementation progress at this organizational level.

To construct the sampling frame, we will use data from multiple sources, including (1) the CCD for the universe of schools (within the sampled school districts) and school level; (2) applications for the School Improvement Grant (SIG) program to identify lists of schools identified as persistently low achieving (PLA); and (3) EDFacts, maintained by ED, for the lists of schools identified as in need of improvement (SINI) under ESEA.

We will draw a sample of 3,800 schools nested within the nationally representative sample of 1,700 school districts. (The universe of schools is 100,640.)

B.2 Information Collection Procedures

Notification of the sample, recruitment, and data collection will proceed as follows.

Introducing the Study to State, District and School Leaders. We will send letters and background materials to Governors and Chief State School Officers (CSSOs) at the state level, Superintendents and Deputy Superintendents in the sampled districts, and principals at the sampled schools to alert them to the study and identify the districts and schools selected for the study sample and provide confidentiality assurances.

Because we anticipate that district surveys will require input from several key individuals, the district letters will ask for contact information for a study liaison to be designated to coordinate identifying and distributing the survey to the appropriate individuals. Once identified, we will conduct all follow up directly with that person. At the state level, each Chief will be responsible for determining whether he or she is in the best position to respond to the questions or whether other state education officials should take the lead in responding to individual sections of the survey.

Follow-Up on Initial Communications. Within 1 week of the initial letters, we will make follow-up telephone calls to CSSOs to confirm receipt of the letter, answer any questions, and ensure their cooperation with the study. We will make follow-up telephone calls to district Superintendents/Deputy Superintendents to confirm receipt of the letter, answer any questions, and confirm the identity of the study liaison. For those districts in our sample, we will follow all required procedures and request approval from central office and school staff (presumably principals). As necessary, we will obtain the approval of the districts either through submission of the required research or in those districts where a research application is not required, the approval to proceed with the school level recruitment.

During the follow up telephone calls at both the state and district level, we will request email addresses for designated contacts.

Administering Surveys. After our initial contact, we will follow up by email with a short explanatory email cover letter and brochure and survey attachments. For contacts without email, we will follow up by priority U.S. mail. The cover letter will explain how to complete the survey. For state surveys, these emails will explain that the attached survey can be completed as an electronic document and returned electronically or printed and completed as a paper-and-pencil instrument to be returned by fax or mail. The district emails will be sent to the study liaison and the school emails will be sent once we obtain district approval to begin school recruitment. The district and school cover letters will clearly explain that respondents have three options for responding to the survey: as a web-based instrument, as an electronic document, and as a paper-and-pencil instrument. They will also include the survey URL and login ID for responding to the survey as a web-based instrument. All letters will include a toll-number for respondents’ questions and technical support.

Nonresponse Followup. We will initiate several forms of follow-up contacts with state, district and school respondents who have not responded to our communication. We will use a combination of reminder postcards, emails and follow up letters to encourage respondents to complete the surveys. The project management system developed for this study will be the primary tool for monitoring whether surveys have been initiated. After 10 days, we will send an email message (or postcard for those without email) to all nonresponders indicating that we have not received a completed survey and encouraging them to submit one soon. Within 7 business days of this first follow up we will mail nonrespondents a hard copy package including all materials in the initial mailing. Ten days after the second followup, we will telephone the remaining nonrespondents to ask that they complete the survey and offer them the option to answer they survey by phone, either at that time or at time to be scheduled during the call.

We expect to obtain an 80 percent response rate from school districts and schools. We expect that all 50 states and DC will participate.

B2.1 Statistical Methodology for Stratification and Sample Selection

Nationally representative sample of school districts

As discussed in B.1, we will draw a nationally representative sample of 1,700 school districts from the 50 states and the District of Columbia. One analytic interest is in comparing the activities of districts with large amounts of ARRA funding (per pupil) with similar districts with lesser (or no) funding. The amount and degree of ARRA funding we anticipate will vary considerably, but most districts will receive at least some funding. A nationally representative sample then should provide a district sample with a range of funding levels.

The district frame is based on the 2008-09 National Center for Education Statistics’ Common Core of Data (CCD) frame, as processed through National Assessment of Educational Progress (NAEP) macros to purge entities that are not in scope (e.g., administrative districts, district consortiums, entities devoted to auxiliary educational services, etc.), as well as a canvassing of new districts from the preliminary 2009-10 CCD frame (only districts with positive enrollments on the CCD frame, with other out-of-scope entities purged out). All school districts and independent charter districts with at least one eligible school and at least one enrolled student will be included in the frame.³

There will be a probability proportionate size (PPS) sample of districts, with number of students as the measure of size. Given the evaluation’s goal of focusing on ARRA funded reform efforts, the major strata will ensure that districts from Race to the Top (RTT) states are represented to reflect their actual population values. The strata include:

RTT winning states (Delaware, District of Columbia, Florida, Georgia, Hawaii, Maryland, Massachusetts, New York, North Carolina, Ohio, Rhode Island, Tennessee);
RTT finalist states (Arizona, California, Colorado, Illinois, Kentucky, Louisiana, New Jersey, Pennsylvania, South Carolina); and
All other states.

The RTT finalist states are states which were round two finalists for Race to the Top funding but did not win. These states should be similar in many ways to the RTT states and can, therefore, provide a key comparison group for analysis. We plan to oversample high-poverty districts. We are defining districts to be high-poverty if they have greater than 16.7 percent of 5 to 17 year olds in poverty, according to estimates for 2008 from the Small Area Income and Poverty Estimate Program (SAIPE).⁴

The oversampling factor for high-poverty districts will be a factor of 2.⁵ Table 1 presents expected student percentages for the three district strata crossed by high-poverty status.⁶ The measure of size for each stratum is proportional to two times the percentage of students for the high-poverty strata, and is proportional to the percentage of students for the low-poverty strata. The allocated sample size is based on this measure of size. We expect 20 percent attrition due to nonresponse. Sample sizes after this expected attrition are presented in the last column to the right.

Table 1. District Sample Design: RTT and Poverty Strata Allocations

Stratum	Poverty stratum	Estimated student count (in 1000s)	Percent of students	Percent of measure of size	Allocation propor-tional to estimated measure of size	Sample size after attrition

RTT Winners	High	5,746	11.72%	16.36%	278	222
RTT Winners	Low	7,797	15.90%	11.10%	189	151
RTT Winners	Total	13,543	27.61%	27.45%	467	373

RTT Finalists	High	7,269	14.82%	20.69%	352	281
RTT Finalists	Low	8,177	16.67%	11.64%	198	158
RTT Finalists	Total	15,447	31.49%	32.33%	550	440

Remainder States	High	8,196	16.71%	23.33%	397	317
Remainder States	Low	11,862	24.19%	16.88%	287	230
Remainder States	Total	20,058	40.90%	40.21%	684	547

Total		49,048	100.00%	100.00%	1,700	1,360

Table 2 presents calculations of normalized standard errors for the two poverty strata, and for the national estimator, based on a completely proportional sample design (no oversampling of high-poverty districts) and the proposed sample design which includes oversampling of high-poverty districts. The middle columns present sample sizes after expected attrition from 20 percent nonresponse and normalized standard errors from a strictly proportional allocation. The final three columns to the right present expected sample sizes after expected attrition and normalized standard errors under the proposed sample design of oversampling high-poverty districts by a factor of 2 (so that the high-poverty districts receive 2/3 of the sample allocation). The normalized standard errors are the standard error as a fraction of the population standard deviation for a particular characteristic of interest at the population level.⁷ For example, a normalized standard error of 2.87 percent means that if the population standard deviation for a characteristic is 100, then the national estimator standard error for this characteristic will be 2.87.

As can be seen, under the proposed design the normalized standard error for high-poverty districts is much lower as compared to proportional allocation. The normalized standard error for low-poverty districts is much higher for the proposed design as compared to proportional allocation, but high-poverty districts are of particular interest for this study. For national estimators, the normalized standard error under the proposed design is a little bit higher than that for a proportional allocation design. This is a small loss of efficiency for the proposed national design in order to achieve a much better result for high-poverty districts. Given the importance of high-poverty districts in this study, this is a tradeoff worth making.

Table 2. Normalized Standard Errors for the Two Poverty Strata

			Proportional sample design		Proposed sample design
District Stratum	Estimated student count (in 1000s)	Percent of students	Propor-tional sample size (after attrition)	Norma-lized standard error	Percent of measure of size	Over-sampling design sample size after attrition	Norma-lized standard error

High-poverty	21,211	43.25%	588	4.12%	60.38%	821	3.49%
Low-poverty	27,837	56.75%	772	3.60%	39.62%	539	4.31%
Total	49,048	100.00%	1,360	2.71%	100.00%	1,360	2.87%

Table 3 presents results for the three primary strata comparing proportional allocation to the proposed design. In this case, a normalized standard error is only presented for the proposed design and a design effect is included, which is equal to the square of the ratio of the normalized standard error of the proposed design to that of a proportional allocation design within each primary stratum. These design effects for the primary strata are very reasonable again as a cost of improving standard errors for the high-poverty strata within each primary stratum.

Table 3. Normalized Standard Errors for the Three Primary Strata

Stratum	Poverty stratum	Percent of students	Sample size after attrition	Normalized standard error	Design effect

RTT Winners	High	42.43%	222	6.70%	1
RTT Winners	Low	57.57%	151	8.14%	1
RTT Winners	Total	100.00%	373	5.48%	1.122

RTT Finalists	High	47.06%	281	5.96%	1
RTT Finalists	Low	52.94%	158	7.95%	1
RTT Finalists	Total	100.00%	440	5.06%	1.125

Remainder States	High	40.86%	317	5.61%	1
Remainder States	Low	59.14%	230	6.60%	1
Remainder States	Total	100.00%	547	4.53%	1.121

Within the RTT stratum, we will stratify first by state to be sure that each RTT winning state had proportional representation. Within the RTT finalist stratum and the remainder stratum, we will stratify first by Census Region to be sure we have geographic representation. Table 4 below presents percentages for each RTT state as a share of all RTT states, as a fraction of student enrollment and as a fraction of the total measure of size (with high-poverty districts doubled as compared to low-poverty districts). The allocated sample size is the overall RTT state sample size of 467 multiplied by the estimated measure of size percentage. The ‘total CCD districts’ is a count of school districts for the state from our district frame. In two cases, the allocated district sample size exceeds the total CCD district count. Hawaii has only one single district covering the entire state, and this will be taken with certainty. Florida and Maryland have a small number of districts given its population, and all districts will be taken in Florida and Maryland as well. Subtracting out the district totals for Florida, Maryland and Hawaii, the remaining sample is 368 (467 minus 99). This sample is reallocated across the remaining RTT states to complete the assigned sample size calculation, as given in the rightmost column of Table 4.

Table 4. Estimated Shares and Expected Sample Sizes for the RTT States

State	Estimated students (in 1000s)	Percent of students	Estimated percent of measure of size	Allocated sample size	Total CCD districts	Assigned sample size

Delaware	125	0.9%	0.8%	4	37	4
District of Columbia	69	0.5%	0.7%	3	56	3
Florida	2,630	19.4%	17.7%	83	73	73
Georgia	1,656	12.2%	12.9%	60	186	62
Hawaii	179	1.3%	0.9%	4	1	1
Maryland	844	6.2%	4.9%	23	25	25
Massachusetts	958	7.1%	6.1%	29	392	29
New York	2,658	19.6%	21.5%	101	855	104
North Carolina	1,489	11.0%	12.0%	56	211	58
Ohio	1,817	13.4%	13.2%	62	942	63
Rhode Island	145	1.1%	1.0%	5	51	5
Tennessee	972	7.2%	8.2%	38	140	39
Total	13,543	100.0%	100.0%	467	2969	467

Table 5 presents similar computations for the RTT finalist and the remainder stratum. Sample sizes after expected nonresponse attrition are also presented. In this case, the strata are by Census Region.

Table 5. Estimated Shares and Expected Sample Sizes for the RTT Finalist and Remainder Stratum States, by Census Region Strata

Stratum	Census Region	Estimated student count (in 1000s)	Percent of students	Percent of measure of size	Projected sample size	Projected sample size after attrition

RTT Finalists	Northeast	3,099	20.06%	17.94%	99	79
RTT Finalists	Central	2,120	13.72%	13.37%	74	59
RTT Finalists	South	2,075	13.43%	15.86%	87	70
RTT Finalists	West	8,153	52.78%	52.82%	291	232
RTT Finalists	Total	15,447	100.00%	100.0%	550	440

Remainder Stratum	Northeast	1,048	5.23%	4.64%	32	25
Remainder Stratum	Central	6,790	33.85%	33.11%	226	181
Remainder Stratum	South	8,624	42.99%	45.41%	311	248
Remainder Stratum	West	3,597	17.93%	16.85%	115	92
Remainder Stratum	Total	20,058	100.00%	100.0%	684	547

The RTT/geography strata (state within the RTT stratum, and Census Region within the RTT finalists and the remainder strata) are the ‘explicit strata:’ the sample sizes are set exactly for each of these strata. The remaining district stratification is ‘implicit:’ it is implemented by a serpentine sorting⁸ within a hierarchy, followed by a systematic sample. Urbanicity stratum is the implicit stratifier within the RTT state stratum and the non-RTT Census Region strata (1—Central City, 2—Urban Fringe, 3—Town, 4—Rural). Urbanicity for each district is provided on the CCD district frame.

Details of District Frame Sampling: Stratification and Oversampling

The following districts will be certainty selections (included automatically in the sample with probability of selection 1):

District of Columbia Public Schools;
The Hawaii Unified Public School District;
All districts in the states of Florida and Maryland; and
All other districts with measures of size exceeding the sampling interval at any point in the iterative process (see below).

Write 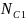as the total number of certainty districts from bullets 1 through 3. The initial measure of size for PPS district sampling is computed as follows. Write as the total number of students in district i and write as the oversampling factor for district i,. The values of are given in Table 6 below. Note, given the evaluation’s focus on reform efforts, the Teacher Incentive Fund (TIF) districts will be oversampled to make sure that at least 70 of these districts are in the district sample.

Table 6. Oversampling Factors by Poverty and TIF Stratum

Poverty Stratum	TIF Stratum	Oversampling Factor
Low Poverty	TIF	1.7
Low Poverty	nonTIF	1
High Poverty	TIF	3.4
High Poverty	nonTIF	2

The measure of size for each district is proportional to 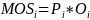. We assign the remaining certainty districts by an iterative process in which each iteration is as follows:

remove the certainty districts already assigned (the original 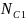plus any certainty districts assigned in earlier iterations),
compute a sampling interval equal to the summation of over the districts left on the frame (those not removed as certainty districts), divided by 1700 minus the total number of currently assigned certainty districts;
designate as certainties any districts whose exceeds the current sampling interval, and
return to step (i).

The iteration stops when there are no further certainties generated. Write 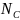as the final number of certainty districts, and SAMP as the final sampling interval. The probability of selection of each district on the noncertainty frame is 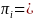)* /SAMP. Note that the summation of 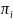is equal to the noncertainty sample size .

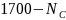The sampling of noncertainty districts will be a systematic sampling process, using the 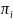as the probabilities of selection, and SAMP as the sampling interval. The ordering of districts for this systematic sample will be hierarchical. The levels of the hierarchy are as follows:

RTT winner/ RTT finalist/ remainder state;
1. Geography (state within RTT winner; Census Region for RTT finalist and remainder state);
  1. Multi-School/ One-School District Status;⁹
    1. Charter/Regular Districts (within One-School Districts only);
      1. TIF/ non TIF status;
        
        Urbanicity (Central City; Urban Fringe; Town; Rural);
        
        Size.

Size will be ordered in a serpentine fashion (largest to smallest, smallest to largest, largest to smallest, etc.), within urbanicity, urbanicity will be ordered in a serpentine fashion within TIF status (central city to rural, rural to central city, central city to rural, etc.), and TIF status will be ordered in a serpentine fashion with Multi-School/ One-school (TIF to non TIF, non TIF to TIF, etc.). Multi-school/One-school status will be ordered in a serpentine fashion within the geographic strata. Census Region will be ordered in a serpentine fashion within the RTT finalist and remainder state strata.

Details of District Frame Sampling: Assignment to the High Poverty Stratum

The high poverty stratum is defined by SAIPE estimates of percentages of 5 to 17 year old children in poverty for the school district. We will compute the mean value of this percentage over all districts in the U.S., and this mean value will become the cutoff.¹⁰ Districts with percentages lower than the cutoff will be designated ‘low poverty’ and districts with percentages higher than the cutoff will be designated ‘high poverty.’ Independent districts such as charter school districts will be associated with the public school district that they are associated with geographically, as only the primary geographically-based public school districts have poverty estimates from SAIPE.

Details of District Frame Sampling: One-School Districts

Any districts with only one school will have a sampling rate set to be 1/4 of the sampling rate they would otherwise receive. We estimate that these districts represent roughly 2 percent of the student population, so without undersampling the district sample would have about 40 sampled districts. (Having districts with only one school is problematic for analyses such as Hierarchical Linear Modeling.) With the undersampling, the expected number will be reduced to a number in the range of 10. These districts will be a separate strata, to control the sample size (so that we do not get too few or too many inadvertently). Even with this undersampling they will still be represented correctly in the population, as their weights will reflect their reduced probabilities of selection (the weights will be 4 times larger than they would otherwise be), but we will have fewer of these districts. This method of undersampling is similar to that done in the National Assessment of Educational Progress for schools with very small numbers of students.

Districts with Persistently Lowest Achieving (PLA) Schools

As discussed in the School Sample Design section below, we have a target sample size of Persistently Lowest Achieving (PLA) schools of 570. This is being drawn from an estimated set of roughly 2,250 of these schools. Many of these schools are in high-poverty districts, so the oversampling of high-poverty districts may yield a large enough set of these schools from which to draw our target sample. Our criterion will be that we wish to guarantee that there will be only a 5 percent chance (or less) that there will be less than 570 PLA schools in the sampled district frame. In order to achieve this goal, it may be necessary to have an extra oversampling rate for districts with at least one PLA school. This oversampling rate, if necessary, will be set in such a way to guarantee this lower bound of 570 expected PLA schools, with at least 95 percent certainty. All districts with at least one PLA school will receive an equal oversampling factor attached to their measure of size (in addition to other factors for high-poverty status and/or TIF status). All of this can only be finalized after the district and school frames are complete, but the sample design will be adjusted up front to make sure that the goals of the study can be achieved,¹¹

Nationally representative subsample of school districts for the polls

We will draw a subsample of one quarter of the district sample (or roughly 400-450 districts) for each of the two polls. The subsamples will be stratified by district strata (urbanicity and poverty status) and grantee status (RTT, TIF, or other). Only respondents to the initial nationally representative sample for the spring surveys will be eligible for this subsampling process; we propose this approach to maximize response rates to the polls, as initial nonrespondents to the spring survey are more likely not to respond to the later polls.

Nationally representative sample of schools

The school sample is a two-phase sample of 3,800 schools, nesting within the sampled districts. We want the school sample to be balanced at the sampled district level, in that the sample sizes are close to the desired sample sizes (e.g., if the expected sample size is 3, then the actual sample size also be three, or at least in the range 2 through 4). This is easy to achieve if districts are the only strata, but we also want balance in terms of:

School level: elementary, middle, and high schools (which is important in light of the current emphasis on high school reform);
School performance status: PLA schools, other schools in need of improvement (SINI), and all other schools; and
School size: small, medium, and large (which allows us to examine whether smaller schools, for example, have the resources to undertake the same types of reform strategies as larger schools).

Overall, this is a multi-dimensional stratification structure. With an average sample size of only 2.2 schools per district (3,800 divided by 1,700), balancing on all of these dimensions simultaneously will be difficult using traditional stratification. A relatively new sampling technique which we propose is called ‘balanced sampling,’ or ‘cube sampling,’ developed in Europe and used, for example, in French Census rotation groups (see for example Deville and Tillé 2004¹²). We will confirm that the algorithm is providing random samples with the desired properties. If Deville and Tillé’s method does not achieve the goal, other methods will be utilized to achieve the desired stratification, or an approximation thereof.¹³

PLA schools will be oversampled due to ARRA’s focus on turning around low performing schools. Our goal is that 15 percent of the sampled schools should be PLA. After checking expected sample sizes, we will define an oversampling factor if it is necessary. Table 7 presents preliminary information about counts of PLA schools and SINI non PLA schools. Our target sample percentages and sample sizes are given.

Oversampling factors will be defined in order to achieve these goals. It should be noted that we expect the oversampling of high-poverty districts to generate a large number of PLA schools, as we expect most PLA schools to be in high-poverty districts. The oversampling factor then necessary to achieve the 15 percent sample size goal may not be large.

Table 7. Estimated Percentages and Target Sample Sizes by School Performance Status

School Performance Status	School count	Percent of schools	Expected sample size propor-tional allocation	Target sample percent of schools	Target school sample size

PLA	2,248	2.40%	91	15.0%	570
SINI non PLA	12,165	12.96%	493	15.0%	570
Other	79,418	84.64%	3,216	70.0%	2,660
Total	93,831	100.0%	3,800	100.0%	3,800

Table 8 presents similar calculations by school grade span, which we define as follows, following the CCD definition:

elementary is defined to have a low grade of PK through 3^rd grade, and a high grade of PK through 8^th grade;
middle is defined to have a low grade of 4^th through 7^th grade, and a high grade of 4^th through 9^th grade;
high school is defined to have a low grade of 7th through 12^th, and a high grade of 12^th only; and
other schools is defined to include all other schools.

Table 8. Estimated percentages and target sample sizes by school grade span

School Grade Span	Estimated students (in 1000s)	Percent of total	Estimated measure of size (in 1000s)	Percent of total	Expected sample size	Expected sample size after attrition
Elementary	21,058	43.25%	33,021	44.95%	1,708	1,366
Middle	9,292	19.08%	14,015	19.08%	725	580
High	13,655	28.04%	18,839	25.64%	975	780
Other schools	4,686	9.62%	7,586	10.33%	392	314
Total	48,691	100.00%	73,461	100.00%	3,800	3,040

NOTE: The student counts are based on an older NAEP frame and the measures of size are based on an assignment of schools to poverty status based on percent free or reduced lunch students from the NAEP frame. This table will be updated based on the current CCD and SAIPE data when the school frame is ready.

Within each of the four grade-span strata, three school-size strata will be generated (small, medium, and large). The cutoffs for enrollment counts will be the weighted terciles within each of the grade-span strata (weighted by student enrollment). For example, for elementary schools, the small-size stratum will consist of schools with enrollments below the 33^rd weighted percentile of enrollment over all elementary schools on the frame.¹⁴ Thus the small-size stratum will represent 33 percent of all enrollment within elementary schools. Similarly, the medium-size stratum for elementary schools will consist of schools with enrollments between the 33^rd and 67^th weighted percentiles of elementary schools.

The balanced sampling procedure will consist of having three levels of stratification:

stratification by sampled districts (with set sample sizes for each sampled district);
stratification by grade-span and school performance status; and
stratification by grade-span and grade-size strata.

The initial measure of size p_ij for each school ij (district i, school j within district i) will be the school enrollment w_ij divided by the district probability of selection 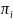. Suppose the stratification cells are subscripted by s=1, 2, 3 (1=districts; 2=school span and school performance status; 3=school span and school size), with stratification cells c_s=1,…,C_s, and assigned sample sizes n_sc (c=1,…,C_s, s=1, 2, 3). The Deville-Tillé balanced sampling algorithm will be used to draw the school sample with these initial measures of size and meeting the three sets stratification cell sample sizes to the extent possible.

B2.2 Estimation Procedures

Please see Part A, Sec. A16 for a discussion of our estimation procedures, and see Part B, Sec. B3 for a discussion of our weighting procedures.

B2.3 Degree of Accuracy Needed

Table 9A below presents power calculations for population percentages for the design for a comparison of districts in RTT states and districts in non RTT states, with sample sizes of 725 and 484 respectively. Under the null hypothesis, the two populations have the same population percentage, and the difference is zero. The difference of sample percentages is an unbiased estimator of the true difference in percentages. The null standard errors for the difference of sample percentages are given in the table assuming simple random sampling within the strata and independent samples.¹⁵ The ‘cutoff for a 95 percent two-sided critical region’ is 1.96 times the null standard error of the difference: the value of the estimated difference for which we will reject the null hypothesis of no difference in the populations. For example, in the first scenario of Table 7A, the critical region for rejection of the null is an absolute value of the difference greater than 5.75 percent (e.g., sample percentages of 50 percent and 44.25 percent for each population would be on the boundary of the critical region). The alternative population percentages provide an alternative hypothesis for which there will be 80 percent power: i.e., there is an 80 percent probability under this alternative of rejecting the null hypothesis. For example, in the first scenario of Table 7A, if the population percentage for non RTT states is 50 percent and the population percentage for RTT states is 41.9 percent, then there is at least an 80 percent chance that the null hypothesis will be rejected (i.e., that the sample percentage difference between non RTT and RTT states will exceed 5.75 percent¹⁶). The probability of failing to reject the null hypothesis in this case is only 20 percent.

Table 9B presents similar calculations, but in this case for the high poverty districts alone (high poverty districts in RTT states versus high poverty districts in non RTT states).

Table 9A. Power calculations for RTT vs. non RTT comparison

	Null Population Percentage	Effective sample size non RTT	Effective sample size RTT	Null standard error of difference	Cutoff for 95% two-sided critical region for difference	Alternative population percentage for non RTT with 80% power	Alternative population percentage for RTT with 80% power
Scenario 1	50%	725	484	2.93%	5.75%	50%	41.9%
Scenario 2	40%	725	484	2.88%	5.64%	40%	32.1%
Scenario 3	30%	725	484	2.69%	5.27%	30%	22.6%
Scenario 4	20%	725	484	2.35%	4.60%	20%	13.6%
Scenario 5	10%	725	484	1.76%	3.45%	10%	5.3%

Table 9B. Power calculations for RTT vs. non RTT comparison within the high poverty districts

	Null Population Percentage	Effective sample size non RTT	Effective sample size RTT	Null standard error of difference	Cutoff for 95% two-sided critical region for difference	Alternative population percentage for non RTT with 80% power	Alternative population percentage for RTT with 80% power
Scenario 1	50%	546	375	3.35%	6.57%	50%	40.7%
Scenario 2	40%	546	375	3.29%	6.44%	40%	31.0%
Scenario 3	30%	546	375	3.07%	6.02%	30%	21.6%
Scenario 4	20%	546	375	2.68%	5.26%	20%	12.7%
Scenario 5	10%	546	375	2.01%	3.94%	10%	4.7%

B2.4 Unusual Problems Requiring Specialized Sampling Procedures

There are no unusual problems requiring specialized sampling procedures.

B2.5 Use of Periodic (less than annual) Data Collection to Reduce Burden

Annual surveys will be conducted over the three-year data collection period in order to assess change over time within the brief period that ARRA funds can be used. The polls, to be conducted twice over the three-year data collection period, will be limited to a smaller sample of school districts and will respond to emerging issues of interest.

B.3 Methods to Maximize Response Rates

To help ensure a high response rate, as the initial step, we will send letters to the sampled respondents (see Appendix E). The letters explain the nature and importance of the evaluation and provides the OMB clearance information, Westat contact information, the URL for the web survey and a username. We will send reminder emails or letters after 2 weeks and again after 4 weeks. Phone follow-up will be used for those individuals who do not respond after the second email reminder or letter. At the same time, we will mail paper copies of the survey to ensure an adequate response rate. We will use a management database to track response rates and identify patterns of nonresponse.

Exhibit 2 summarizes the strategies we will undertake to maximize response rates. With these strategies being employed we expect an 80% response rate from schools, and 80% response rate from districts, and a 100% response rate from states.

Exhibit 2. Strategies to Maximize Response Rates

Advance notification of survey	Gain support and cooperation of district and state administrators by providing advance notice of the survey
Provide clear instructions and user-friendly materials	For state-level surveys: send individually-labeled survey packets with: 1) introductory letter from ED; 2) Survey and cover page that includes purpose of the study, provisions to protect respondents’ privacy and confidentiality; a toll-free telephone number to call for questions; and 3) a postage-paid return envelope For district and school level surveys: send introductory letter from ED along with a personalized cover letter that explains the survey and what participation entails, provides assurance of confidentiality, and provides the web address for the on-line survey along with instructions for completing the on-line survey.
Offer technical assistance for survey respondents	Provide toll-free technical assistance telephone number
Monitor progress regularly	Produce weekly data collection report of completed surveys Maintain regular contact between study team members to monitor response rates, identify non-respondents, and resolve problems Use follow-up and reminder calls and e-mails to non-respondents

Weighting the district and school samples

After completion of field collection in each year, we plan to weight the data to provide a nationally representative estimator. Replicate weights will be generated to provide consistent jackknife replicate variance estimators (statistical packages such as STATA and SAS Version 9.2 allow for easy computation of replicate variance estimates). The development of replicate weights will facilitate the computation of standard errors for the complex analyses necessary for this survey. The replicates will be based fundamentally on the first-phase district sample (so that each replicate is associated with one set of ‘dropped’ districts), but the school weights will need to be carefully calibrated to provide school-level replicate weights that correctly reflect the effects of the balanced sampling process (the replicate weights are recalibrated to add to the stratum totals). We anticipate nonresponse, which we will adjust for by utilizing information about the nonresponding districts and schools from the frame and other sources regarding funding and other important district and school characteristics. This information will be used to generate nonresponse cells with differential response rates. The nonresponse adjustments will be equal to the inverse of the weighted response rate. This will adjust for bias from nonresponse.

B.4 Test of Procedures

The state survey will be pre-tested with nine or fewer state officials. The school district survey and the poll will be pre-tested with nine or fewer district officials. The school survey will be pre-tested with nine or fewer school officials.

B.5 Individuals Consulted on Statistical Aspects of Design

The statistical aspects of the design have been reviewed by staff at the Institute of Education Sciences. The individuals most closely involved in developing the statistical procedures include:

Marsha Silverberg, IES, Project Officer, 202-208-7178

Meredith Bachman, IES, 202-219-2014

Babette Gutmann, Westat, project director, 301-738-3626

Patty Troppe, Westat, deputy project director, 301-294-3924

Lou Rizzo, Westat, senior statistician, 301-294-4486

Juanita Lucas-McLean, director of data collection, 301-294-2866

Bruce Haslam, Policy Studies Associates, director of design, 202-939-5333

Michael Puma, Chesapeake Research Associates, director of analysis, 410-897-4968

Sharon Lohr, Arizona State University, member of Technical Working Group, 480-965-4440

Thomas Cook, Northwestern University, member of Technical Working Group, 847-491-3776

1 The degree to which the State Fiscal Stabilization Fund and bolstering of already established programs (e.g., IDEA) successfully saved and created new education jobs is of policy interest as well. However, (a) this topic has been examined in other forums and (b) at the time when this study is fielded, funds tied to job retention and creation are unlikely to still be available to states, districts, and schools.

2 If additional evaluation resources are available, IES may consider an additional round of data collection in 2014 to more fully capture how implementation efforts change after ARRA funds are spent down.

3 In defining district eligibility, we follow the criteria from the National Assessment of Educational Progress (NAEP). The NAEP macros for excluding districts are applied also in the generation of the district frame here.

4 This cutoff is the mean percentage of 5 to 17 year olds in poverty across SAIPE school districts in 2008.

5 These are tentative assignments based on preliminary frame calculations. We may make limited modifications of these when we have data from the fully complete frame, if some of our expectations are found to be in need of modification.

6 The student counts for the three RTT strata are from the preliminary district frame derived from 2008-09 and 2009-10 CCD frames. The percentages for the high and low poverty stratum within each RTT stratum are taken from the 2008 SAIPE district file.

7 A weighted estimate for a district-level characteristic from a PPS sample of districts (with weight equal to measure of size divided by probability of selection) has a standard error essentially equivalent to that of a simple random sample (see for example Equation 9A.22 of Cochran 1977 (Cochran, W. G. (1977), Sampling Techniques, 3^rd ed., New York: John Wiley & Sons)). 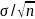Under simple random sampling, if is the population variance, then the standard error is , and the normalized standard error is / = . Note that this ignores the beneficial effects of stratification within each of the three major strata: the standard errors in Table 1 are conservative (a slight overestimate).

8 This sorts within each higher-level stratum as lowest to highest, highest to lowest, lowest to highest, etc. The intention is to spread the distribution across the sort as much as possible when a systematic sort is carried out.

9 One-school districts are districts with only one school. These will be undersampled by a factor of ¼: see the section on one-school districts below.

10 From American Fact Finder on the US Census website, the American Community Survey percentage of 5 to 17 year olds in poverty is 17.0 percent for 2008 and 18.7 percent in 2009. Aggregating poverty percentages over the 13,742 school districts on the 2008 SAIPE file gives a poverty rate of 16.7 percent. This poverty rate will be used as the cutoff for determining high vs. low poverty status. It should be noted that the weighted median over the SAIPE school districts is 15.2 percent, so that there will be more than 50 percent student population in the low-poverty districts (actually 56.8 percent, see Table 2).

11 What we will not do is carry out a rejective procedure of drawing samples and discarding them if they do not have the necessary characteristics. One and only one sample will be drawn, and it will be accepted. This will maintain the integrity of the sample design.

12 Deville, J.-C., and Tillé, Y. (2004). Efficient balanced sampling: The cube method. Biometrika 91, 4, 893-912.

13 What we will not do is a controlled selection approach where the sampling is not truly randomized. Our final sampling plan will meet the stratification requirements at least approximately while remaining fully randomized, with known inclusion probabilities for each school on the frame.

14 The school frame actually consists of the schools within the 1,700 sampled districts, which are then weighted by the inverse of the district probability of selection.

15 This is sqrt (P₀*(1-P₀)*((1/n₁)+(1/n₂))), where P₀ is the null population percentage, n₁ is the effective sample size in non RTT states, and n₂ is the effective sample size in RTT states.

16 The standard error of the difference under the alternative hypothesis is sqrt ((P₁*(1-P₁)/n₁)+ (P₂*(1-P₂)/n₂)), where P₁ is the non RTT population percentage, n₁ is the sample size in non RTT states, P₂ is the RTT population percentage, and n₂ is the sample size in RTT states.

File Type	application/vnd.openxmlformats-officedocument.wordprocessingml.document
File Title	Abt Double-Sided Body Template
Author	Abt Associates Inc
File Modified	0000-00-00
File Created	2021-02-01