ARRA OMB for Recruitment Part B after 60 day public notice rev

This package is the first of three for the Integrated Evaluation of ARRA Funding, Implementation, and Outcomes. Our initial request seeks approval for execution of a sampling plan and recruitment of the selected sites. Subsequent packages will request approval for: (1) an initial round of data collection that will include surveys of all states and a nationally representative sample of districts and schools in spring 2011, and (2) follow up surveys with the same groups in 2012 and 2013. A fast response from OMB is critical if the study is to field the spring 2011 surveys successfully, since much preparation work is necessary to ensure a high response rate from sampled school districts and schools.

Introduction

On February 17, 2009, President Obama signed the American Recovery and Reinvestment Act (ARRA) into law (Pub. L. 111-5). ARRA provides an unprecedented $100 billion of additional funding for the U.S. Department of Education (ED) to administer. While the initial goal of this money is to deliver emergency education funding to states, ARRA is also being used as an opportunity to spur innovation and reform at different levels of the U.S. educational system. Specifically, ARRA requires those receiving grant funds to commit to four core reforms (the four “assurances”): (1) adopting rigorous college-ready and career ready standards and high quality assessments, (2) establishing data systems and using data to improve performance, (3) increasing teacher effectiveness and the equitable distribution of effective teachers, and (4) turning around the lowest performing schools. Investment in these innovative strategies is intended to lead to improved results for students, long-term gains in school and local education agency (LEA) capacity for success, and increased productivity and effectiveness.

The education component of ARRA consists of several grant programs targeting states and LEAs and, in some cases, consortia led by non-profit organizations. The programs under ARRA fall into three general categories: (1) existing programs that received an infusion of funds (e.g., Individuals with Disabilities Education Act, Parts B & C; Title I; State Educational Technology grants; Statewide Longitudinal Data Systems grants); (2) a new program intended mainly for economic stabilization (i.e., State Fiscal Stabilization Fund); and (3) newly created programs that are reform-oriented in nature. Due to the number and scope of these programs, a large proportion of districts and schools across the country will get some ARRA funding. In turn, ARRA represents a unique opportunity to encourage the adoption of school improvement focused reforms and to learn from reform initiatives as they take place.

Although ARRA funds are being disbursed through different grant programs, their goals and strategies are complementary if not overlapping, as are the likely recipients of the funds. For this reason, an evaluative approach where data collection and analysis occurs across grant programs (i.e., it is “integrated”), rather than separately for each set of grantees will not only reduce respondent burden but will also provide critical information about the effect of ARRA as a whole.

Overview of the Study

The Integrated Evaluation of ARRA Funding, Implementation and Outcomes is being conducted under the Institute of Education Sciences (IES), ED’s independent research and evaluation arm. The study is one of several that IES will carry out to examine ARRA’s effects on education (see Exhibit 1).

Exhibit 1. IES Evaluation of ARRA’s Effects on Education

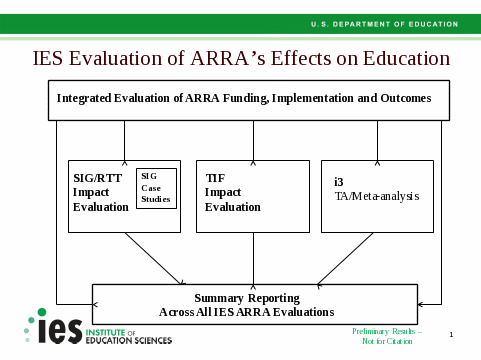
Shape1

The Integrated Evaluation is designed to assess how ARRA efforts are unfolding over time and is therefore primarily descriptive. While information will be gathered on many of the grant programs, the evaluation will focus primarily on the reform-oriented programs (e.g., Race to the Top (RTT), Title I School Improvement Grants (SIG), Investing in Innovation (i3), and the Teacher Incentive Fund (TIF)) since those are of the greatest policy interest¹. The study will support the various impact evaluations IES is conducting by providing critical context for those strategies being rigorously investigated – e.g., by documenting the relative frequency with which they are being implemented across the country, whether they are unique to the particular grant programs, and how they are being combined with other reform approaches.

To achieve these objectives, the Integrated Evaluation will draw heavily on existing information (grant funding allocations, district and school outcomes databases, performance reporting where available) and administer new surveys to all 50 states and to a nationally representative survey of districts and schools. The surveys will be conducted annually for at least three years, in spring 2011, 2012, and 2013.² In addition, two polls of a subsample of sampled districts will be conducted between the 2011 and 2012 and between the 2012 and 2013 larger surveys to capture key, evolving issues of interest to ED officials and other policy makers as they consider shifting technical assistance efforts and further legislative action.

B.1 Respondent Universe and Sampling Methods

We will administer surveys to states, school districts, and schools. The assembly of a universe frame and sampling plan for each is described below, providing the expected numbers of respondents to be included in the recruitment efforts for which we are currently seeking clearance.

State Surveys

We will survey all 50 states and the District of Columbia; there is no sampling proposed for the state survey.

School District Surveys

We will construct a respondent pool and implement a sampling approach for each of the following:

A nationally representative sample of districts, with oversampling of certain ARRA program grantees, in order to track funding and implementation progress at this organizational level; and

A small nationally representative subsample of the nationally representative district sample, in order to obtain information on pressing policy and implementation concerns that might help ED refine technical assistance and legislative plans.

Nationally representative sample of school districts

We will draw a nationally representative sample of districts because ARRA is intended to stimulate broad system change and because, looking across all the ARRA programs, the expected recipients of funds are likely to include most districts. We anticipate that the amount and degree of ARRA funding will vary considerably, but most districts will receive at least some funding. A nationally representative sample then should provide a district sample with a range of funding levels. This sample will be augmented with a sample of districts that are grantees or subgrantees from two of the competitive ARRA programs – Race to the Top (RTT) and the Teacher Incentive Fund cohort 3 (TIF3) – because there is considerable policy interest in the types of reforms being undertaken in school districts that receive RTT and TIF funds in comparison to school districts that do not receive these funds, which are focused on the assurances of educator effectiveness and turning around low performing schools.

We will draw a probability proportionate to size (PPS) sample of districts, with number of students as the measure of size. This PPS sample design will be most efficient for district level estimators which are weighted by number of students. Using PPS designs is the most common and cost effective approach for selecting nationally representative samples.

To construct the sampling frame, we will use data from multiple sources, including (1) the National Center for Education Statistics’ Common Core of Data (CCD) for the universe of school districts, number of students, urbanicity, and poverty status; and (2) lists from ED on the TIF3 grantees.

We will draw a sample of 1,700 school districts out of 16,398 school districts.

Nationally representative subsample of school districts for polls

For each of the two polls, we will draw a random subsample of one quarter of the nationally representative sample of school districts, resulting in 400-450 districts in each subsample. School districts selected to receive the first poll will not be included in the sample to receive the second poll so that no district is unduly burdened by two polls.

School Surveys

We will construct a respondent pool and implement a sampling approach for:

A nationally representative sample of schools, with oversampling of schools likely to be affected by ARRA programs, in order to track funding and implementation progress at this organizational level.

To construct the sampling frame, we will use data from multiple sources, including (1) the CCD for the universe of schools (within the sampled school districts) and school level; (2) applications for the School Improvement Grant (SIG) program to identify lists of schools identified as persistently low achieving (PLA); and (3) EDFacts, maintained by ED, for the lists of schools identified as in need of improvement (SINI) under ESEA.

We will draw a sample of 3,800 schools nested within the nationally representative sample of 1,700 school districts. (The universe of schools is 100,640.)

B.2 Information Collection Procedures

Notification of the sample, recruitment, and data collection will proceed as follows.

Introducing the Study to State, District and School Leaders. We will send letters and background materials to Governors and Chief State School Officers (CSSOs) at the state level, Superintendents and Deputy Superintendents in the sampled districts, and principals at the sampled schools to alert them to the study and identify the districts and schools selected for the study sample and provide confidentiality assurances. These letters are discussed in Part A and included as an appendix to Part A.

Because we anticipate that district surveys will require input from several key individuals, the district letters will ask for contact information for a study liaison to be designated to coordinate identifying and distributing the survey to the appropriate individuals. Once identified, we will conduct all follow up directly with that person. At the state level, each Chief will be responsible for determining whether he or she is in the best position to respond to the questions or whether other state education officials should take the lead in responding to individual sections of the survey.

Follow-Up on Initial Communications. Within 1 week of the initial letters, we will make follow-up telephone calls to CSSOs to confirm receipt of the letter, answer any questions, and ensure their cooperation with the study. We will make follow-up telephone calls to district Superintendents/Deputy Superintendents to confirm receipt of the letter, answer any questions, and confirm the identity of the study liaison. For those districts in our sample, we will follow all required procedures and request approval from central office and school staff (presumably principals). As necessary, we will obtain the approval of the districts either through submission of the required research or in those districts where a research application is not required, the approval to proceed with the school level recruitment.

During the follow up telephone calls at both the state and district level, we will request email addresses for designated contacts.

Administering Surveys. After our initial contact, we will follow up by email with a short explanatory email cover letter and brochure and survey attachments. For contacts without email, we will follow up by priority U.S. mail. The cover letter will explain how to complete the survey. For state surveys, these emails will explain that the attached survey can be completed as an electronic document and returned electronically or printed and completed as a paper-and-pencil instrument to be returned by fax or mail. The district emails will be sent to the study liaison and the school emails will be sent once we obtain district approval to begin school recruitment. The district and school cover letters will clearly explain that respondents have three options for responding to the survey: as a web-based instrument, as an electronic document, and as a paper-and-pencil instrument. They will also include the survey URL and login ID for responding to the survey as a web-based instrument. All letters will include a toll-number for respondents’ questions and technical support.

Nonresponse Followup. We will initiate several forms of follow-up contacts with state, district and school respondents who have not responded to our communication. We will use a combination of reminder postcards, emails and follow up letters to encourage respondents to complete the surveys. The project management system developed for this study will be the primary tool for monitoring whether surveys have been initiated. After 10 days, we will send an email message (or postcard for those without email) to all nonresponders indicating that we have not received a completed survey and encouraging them to submit one soon. Within 7 business days of this first follow up we will mail nonrespondents a hard copy package including all materials in the initial mailing. Ten days after the second followup, we will telephone the remaining nonrespondents to ask that they complete the survey and offer them the option to answer they survey by phone, either at that time or at time to be scheduled during the call.

We expect to obtain an 80 percent response rate from school districts and schools. We expect that all 50 states and DC will participate.

B2.1 Statistical Methodology for Stratification and Sample Selection

Nationally representative sample of school districts

As discussed in B.1, we will draw a nationally representative sample of 1,700 school districts from the 50 states and the District of Columbia. One analytic interest is in comparing the activities of districts with large amounts of ARRA funding (per pupil) with similar districts with lesser (or no) funding. The amount and degree of ARRA funding we anticipate will vary considerably, but most districts will receive at least some funding. A nationally representative sample then should provide a district sample with a range of funding levels.

There will be a probability proportionate size (PPS) sample of districts, with number of students as the measure of size. The major strata will be RTT states vs. non RTT states, as this is a key comparison for analysis. We will oversample districts in RTT states, and we will oversample high-poverty districts in both the RTT state stratum and the non RTT state stratum. We are oversampling high poverty districts because we believe they are most likely to receive the bulk of ARRA funding and overlap significantly with districts that receive SIG funds, where there is expected to be substantial efforts to turn around low performing schools – another key policy interest. We are defining districts to be high-poverty if they have greater than 40 percent of their students eligible for free or reduced lunches³. The oversampling factor for districts in RTT states will be 1.7 and the oversampling factor for high-poverty districts will be 2. These rates are carefully selected to provide a larger set of both districts in RTT states and high-poverty districts, while not reducing the effective sample sizes for national samples by too great a degree.

Table 1A below presents expected percentages of students, oversampling rates, expected sample sizes with the oversampling rates, and expected sample sizes after expected nonresponse attrition (we are expecting a 20 percent nonresponse). Table 1B summarizes Table 1A across poverty strata.

Table 1A. Expected percentages and sample sizes for district sample design: RTT and poverty strata

RTT stratum	Poverty stratum	Estimated students (in 1000s)	Percent of total	Expected sample size prptnl alloc	Over-sam-pling rate	Expected sample size with over-sampling	Expected sample size after attrition	Effective sample size

non RTT States	High-poverty	17,689	36.3%	618	2.0	683	546	546
non RTT States	Low-poverty	17,394	35.7%	607	1.0	336	269	269
non RTT States	Total	35,082	72.1%	1,225		1,019	815	725

RTT States	High-poverty	7,140	14.7%	249	3.4	469	375	375
RTT States	Low-poverty	6,470	13.3%	226	1.7	212	170	170
RTT States	Total	13,609	27.9%	475		681	545	484

Total	Total	48,691	100.0%	1,700		1,700	1,360	1,139

Table 1B. District Sample Design: RTT state and non RTT state strata

RTT stratum	Estimated students (in 1000s)	Percent	Expected sample size proportional allocation	Expected sample size with over-sampling	Percent of sample	Expected sample size with attrition (20% non-response)	Effective sample size
non RTT States	35,082	72.1%	1,225	1,019	60.3%	815	725
RTT States	13,609	27.9%	475	681	39.7%	545	484
Total	48,691	100.0%	1,700	1,700	100.0%	1,360	1,139

As can be seen in Tables 1A and 1B, the RTT states represent 28 percent of the public school students in the US. A completely proportional allocation would result in an expected sample size of 475 districts in RTT states. Given the importance of the comparisons we want to be able to make between districts in RTT states and districts in non RTT states, an oversampling of RTT states will be undertaken. Using an oversampling rate of 1.7 (as shown in Table 1A), the sample percentage of districts in RTT state is 40 percent. This will result in an expected number of 681 districts in RTT states, improving this number from the proportional allocation figure of 475.

A proportional allocation will provide a high-poverty district expected sample size of 867 (see Table 1A: the summation of 618 and 249). Given the importance of the high-poverty group of districts in these reform efforts, this is not an adequate sample size. Using an oversampling rate of 2.0 for the high-poverty districts, the expected sample size of high-poverty districts rises to 1,152. There is some loss of efficiency in the nationally representative district sample from this oversampling. High poverty districts in RTT states are actually being oversampled at a rate of 3.4 (2 times 1.7).

After expected attrition from nonresponse, we expect a district sample size of 1,360. The effective sample size accounting for the oversampling plan is 1,139, a design effect of 1.2.⁴

Within the RTT stratum, we will stratify first by state. Table 2 below presents percentages for each RTT state as a share of all RTT states, as a fraction of student enrollment and as a fraction of measure of size, where measure of size is computed as 2 times enrollment for high-poverty districts, 1 times enrollment for low-poverty districts, and 1.5 times enrollment for districts with unknown poverty status at this stage of preliminary frame development (primarily Ohio). The ‘expected sample size proportional allocation’ is an allocation of the 681 sample size for RTT states based on the measure of size percentages for each state, ‘regular school districts’ is a preliminary count of regular school districts for the state, and ‘expected sample size’ is equal to the regular school district count if the proportional allocation sample size exceeds the regular school district (these states become ‘certainty states’: all districts are taken with certainty into the sample), and is a reallocated sample size for the remaining states (subtracting out the certainty states from both sample size and measure of size totals).

District of Columbia and Hawaii are both certainty states: their single regular school district will be included with certainty in the district sample. Florida and Maryland have small numbers of regular school districts as compared to their populations, so they will also be certainty states (all regular school districts are included). The remaining eight RTT states will have samples drawn, with expected sample sizes given in Table 2.

Within the non RTT stratum, we will stratify first by Census Region, because we hypothesize that there might be different fiscal condition and types or levels of activities across the regions and to ensure a broad distribution of districts (see Table 3).

The RTT/geography strata (state within RTT, Census Region within non RTT) are the ‘explicit strata:’ the sample sizes are set exactly for each of these strata.

The remaining district stratification is ‘implicit:’ it is implemented by a serpentine sorting⁵ within a hierarchy, followed by a systematic sample. Urbanicity stratum is the implicit stratifier within RTT state and non RTT Census Region (1—Central City, 2—Urban Fringe, 3—Town, 4—Rural).

Table 2. Estimated shares and expected sample sizes for the RTT states

RTT States	Estimated students (in 1000s)	Percent of RTT stratum	High-poverty weighted percent	Expected sample size proportional allocation	Regular School Districts	Expected sample size
Delaware	123	0.9%	0.8%	6	19	7
District of Columbia	77	0.6%	0.7%	4	1	1
Florida	2,646	19.4%	20.0%	136	67	67
Georgia	1,648	12.1%	13.2%	90	180	107
Hawaii	180	1.3%	1.2%	9	1	1
Maryland	844	6.2%	5.5%	37	24	24
Massachusetts	962	7.1%	6.1%	41	244	49
New York	2,752	20.2%	19.7%	134	696	160
North Carolina	1,457	10.7%	11.0%	75	116	89
Ohio	1,812	13.3%	13.1%	89	613	106
Rhode Island	146	1.1%	1.0%	7	32	8
Tennessee	963	7.1%	7.7%	52	136	62
Total	13,610	100.0%	100.0%	681		681

NOTE: The totals, percentages, and expected sample sizes are all based on a preliminary frame, and will be modified after the frame is finalized.

Table 3. Sample size allocations for non RTT states by Census Region

Census Region	Estimated students (in 1000s)	Percent of RTT stratum	High-poverty weighted percent	Expected sample size proportional allocation
Northeast	4,194	12.0%	10.4%	106
Central	8,863	25.3%	23.5%	239
South	10,588	30.2%	32.7%	333
West	11,437	32.6%	33.5%	341
Total	35,082	100.0%	100.0%	1,019

NOTE: The totals, percentages, and expected sample sizes are all based on a preliminary frame, and will be modified after the frame is finalized.

Urbanicity for districts is defined based on student plurality: the urbanicity for the largest number of students in the district becomes the urbanicity value for the district for stratification purposes. Urbanicity at the school level is obtained from Census urbanicity definitions for the zip code area containing the school. Table 4 below presents expected student estimates, measures of size (doubled for high-poverty districts), and expected sample sizes for the four urbanicity categories for the RTT states and the non RTT states.

Table 4. Estimated shares and expected sample sizes by urbanicity

RTT stratum	Urbanicity	Estimated students (in 1000s)	Percent of total	Estimated measure of size (in 1000s)	Percent of total	Expected sample size	Expected sample size after attrition

non RTT States	Central City	10,668	30.4%	17,697	33.5%	342	273
non RTT States	Urban Fringe	11,580	33.0%	15,828	30.0%	306	245
non RTT States	Town	4,826	13.8%	7,614	14.4%	147	118
non RTT States	Rural	8,007	22.8%	11,629	22.0%	225	180
non RTT States	Total	35,082	100.0%	52,768	100.0%	1,019	815

RTT States	Central City	3,619	26.6%	6,199	30.0%	204	163
RTT States	Urban Fringe	5,479	40.3%	7,660	37.0%	252	202
RTT States	Town	1,300	9.6%	2,088	10.1%	69	55
RTT States	Rural	3,211	23.6%	4,746	22.9%	156	125
RTT States	Total	13,609	100.0%	20,692	100.0%	681	545

Total	Total	48,691	100.0%	73,460		1,700	1,360

Nationally representative subsample of school districts for the polls

We will draw a subsample of one quarter of the district sample (or roughly 400-450 districts) for each of the two polls. The subsamples will be stratified by district strata (urbanicity and poverty status) and grantee status (RTT, TIF, or other). Only respondents to the initial nationally representative sample for the spring surveys will be eligible for this subsampling process; we propose this approach to maximize response rates to the polls, as initial nonrespondents to the spring survey are more likely not to respond to the later polls.

Nationally representative sample of schools

The school sample is a two-phase sample of 3,800 schools, nesting within the sampled districts. The school sample will be selected using a statistical method called balanced sampling, which will control the district level school sample size within the range of 2 to 3 while at the same time balancing across the stratification levels. Across the entire national school sample, we will ensure a balance on three stratification levels:

School level: elementary, middle, and high;

School performance: persistently low achieving (PLA) schools, other schools in need of improvement (SINI), and all other schools; and

School size.

Our plan is that the school sample will be balanced at the sampled district level, in that the sample sizes are close to the desired sample sizes (e.g., if the expected sample size is 3, then the actual sample size also be three, or at least in the range 2 through 4). This is easy to achieve if districts are the only strata, but we also want balance in terms of school level, school performance status, and school size), and urbanicity. Overall, this is a multi-dimensional stratification structure. With an average sample size of only 2.2 schools per district (3,800 divided by 1,700), balancing on all of these dimensions simultaneously will be difficult using traditional stratification. A relatively new sampling technique which we will use is called ‘balanced sampling,’ or ‘cube sampling,’ developed in Europe and used, for example, in French Census rotation groups (see for example Deville and Tillé 2004⁶).

PLA schools will be oversampled, as these schools are a particular focus of the ARRA programs. Our goal is that 15 percent of the sampled schools should be PLA. Table 5 presents preliminary information about counts of PLA schools and SINI non PLA schools for RTT states and non RTT states respectively. Our target sample percentages and sample sizes are given.

Table 5. Estimated percentages and target sample sizes by school performance status

Stratum	School Performance Status	School count	Percent of schools	Expected sample size proportional allocation	Target sample percent of schools	Target school sample size

non RTT States	PLA	1,802	2.53%	58	15.00%	342
non RTT States	SINI non PLA	8,519	11.98%	273	15.00%	342
non RTT States	Other	60,815	85.49%	1,947	70.00%	1,594
non RTT States	Total	71,136	100.00%	2,278	100.00%	2,278

RTT States	PLA	446	1.97%	30	15.00%	228
RTT States	SINI non PLA	3,646	16.07%	245	15.00%	228
RTT States	Other	18,603	81.97%	1,248	70.00%	1,066
RTT States	Total	22,695	100.00%	1,522	100.00%	1,522

Total	Total	93,831		3,800		3,800

Oversampling factors will be defined in order to achieve these goals. It should be noted that we expect the oversampling of high poverty districts to generate a large number of PLA schools, as we expect most PLA schools to be in high poverty districts. The oversampling factor then necessary to achieve the 15 percent sample size goal may not be large.

Table 6 presents similar calculations by school grade span, which we define as follows:

elementary is defined to have at least one of grades 1 through 4, and no grade higher than grade 7;
middle is defined to have at least one of grades 7 and 8, no grade lower than grade 5 and no grade higher than grade 9;
high school is defined to have at least one of grades 10 through 12, and no grade lower than grade 9; and
other schools is defined to include all other schools.

Table 6. Estimated percentages and target sample sizes by school grade span

RTT stratum	School Grade Span	Estimated students (in 1000s)	Percent of total	Estimated measure of size (in 1000s)	Percent of total	Expected sample size	Expected sample size after attrition

non RTT States	Elementary	15,153	43.2%	23,717	44.9%	1,024	819
non RTT States	Middle	6,604	18.8%	9,884	18.7%	427	341
non RTT States	High	9,800	27.9%	13,428	25.4%	580	464
non RTT States	Other schools	3,524	10.0%	5,739	10.9%	248	198
non RTT States	Total	35,082	100.0%	52,768	100.0%	2,278	1,822

RTT States	Elementary	5,905	43.4%	9,304	45.0%	684	548
RTT States	Middle	2,688	19.7%	4,131	20.0%	304	243
RTT States	High	3,855	28.3%	5,411	26.1%	398	318
RTT States	Other schools	1,162	8.5%	1,847	8.9%	136	109
RTT States	Total	13,609	100.0%	20,692	100.0%	1,522	1,218

Total	Total	48,691	100.0%	73,460		3,800	3,040

B2.2 Estimation Procedures

Please see Part A, Sec. A16 for a discussion.

B2.3 Degree of Accuracy Needed

Table 7A below presents power calculations for population percentages for the design for a comparison of districts in RTT states and districts in non RTT states, with sample sizes of 725 and 484 respectively. Under the null hypothesis, the two populations have the same population percentage, and the difference is zero. The difference of sample percentages is an unbiased estimator of the true difference in percentages. The null standard errors for the difference of sample percentages are given in the table assuming simple random sampling within the strata and independent samples.⁷ The ‘cutoff for a 95 percent two-sided critical region’ is 1.96 times the null standard error of the difference: the value of the estimated difference for which we will reject the null hypothesis of no difference in the populations. For example, in the first scenario of Table 7A, the critical region for rejection of the null is an absolute value of the difference greater than 5.75 percent (e.g., sample percentages of 50 percent and 44.25 percent for each population would be on the boundary of the critical region). The alternative population percentages provide an alternative hypothesis for which there will be 80 percent power: i.e., there is an 80 percent probability under this alternative of rejecting the null hypothesis. For example, in the first scenario of Table 7A, if the population percentage for non RTT states is 50 percent and the population percentage for RTT states is 41.9 percent, then there is at least an 80 percent chance that the null hypothesis will be rejected (i.e., that the sample percentage difference between non RTT and RTT states will exceed 5.75 percent⁸). The probability of failing to reject the null hypothesis in this case is only 20 percent.

Table 7B presents similar calculations, but in this case for the high poverty districts alone (high poverty districts in RTT states versus high poverty districts in non RTT states).

Table 7A. Power calculations for RTT vs. non RTT comparison

	Null Population Percentage	Effective sample size non RTT	Effective sample size RTT	Null standard error of difference	Cutoff for 95% two-sided critical region for difference	Alternative population percentage for non RTT with 80% power	Alternative population percentage for RTT with 80% power
Scenario 1	50%	725	484	2.93%	5.75%	50%	41.9%
Scenario 2	40%	725	484	2.88%	5.64%	40%	32.1%
Scenario 3	30%	725	484	2.69%	5.27%	30%	22.6%
Scenario 4	20%	725	484	2.35%	4.60%	20%	13.6%
Scenario 5	10%	725	484	1.76%	3.45%	10%	5.3%

Table 7B. Power calculations for RTT vs. non RTT comparison within the high poverty districts

	Null Population Percentage	Effective sample size non RTT	Effective sample size RTT	Null standard error of difference	Cutoff for 95% two-sided critical region for difference	Alternative population percentage for non RTT with 80% power	Alternative population percentage for RTT with 80% power
Scenario 1	50%	546	375	3.35%	6.57%	50%	40.7%
Scenario 2	40%	546	375	3.29%	6.44%	40%	31.0%
Scenario 3	30%	546	375	3.07%	6.02%	30%	21.6%
Scenario 4	20%	546	375	2.68%	5.26%	20%	12.7%
Scenario 5	10%	546	375	2.01%	3.94%	10%	4.7%

B2.4 Unusual Problems Requiring Specialized Sampling Procedures

There are no unusual problems requiring specialized sampling procedures.

B2.5 Use of Periodic (less than annual) Data Collection to Reduce Burden

Annual surveys will be conducted over the three-year data collection period in order to assess change over time within the brief period that ARRA funds can be used. The polls, to be conducted twice over the three-year data collection period, will be limited to a smaller sample of school districts and will respond to emerging issues of interest.

B.3 Methods to Maximize Response Rates

To help ensure a high response rate, as the initial step, we will send two letters to the sampled respondents, the first on ED letterhead signed by Secretary Duncan that explains the nature and importance of the evaluation, and the second on Westat letterhead that provides the OMB clearance information, Westat contact information, the URL for the web survey and a username. We will send reminder emails or letters after 2 weeks and again after 4 weeks. Phone follow-up will be used for those individuals who do not respond after the second email reminder or letter. At the same time, we will mail paper copies of the survey to ensure an adequate response rate. We will use a management database to track response rates and identify patterns of nonresponse. Exhibit 2 summarizes the strategies we will undertake to maximize response rates.

Exhibit 2. Strategies to Maximize Response Rates

Advance notification of survey	Gain support and cooperation of district and state administrators by providing advance notice of the survey
Provide clear instructions and user-friendly materials	For state-level surveys: send individually-labeled survey packets with: 1) introductory letter from ED; 2) Survey and cover page that includes purpose of the study, provisions to protect respondents’ privacy and confidentiality; a toll-free telephone number to call for questions; and 3) a postage-paid return envelope For district and school level surveys: send introductory letter from ED along with a personalized cover letter that explains the survey and what participation entails, provides assurance of confidentiality, and provides the web address for the on-line survey along with instructions for completing the on-line survey.
Offer technical assistance for survey respondents	Provide toll-free technical assistance telephone number
Monitor progress regularly	Produce weekly data collection report of completed surveys Maintain regular contact between study team members to monitor response rates, identify non-respondents, and resolve problems Use follow-up and reminder calls and e-mails to non-respondents

Weighting the district and school samples

After completion of field collection in each year, we plan to weight the data to provide a nationally representative estimator. Replicate weights will be generated to provide consistent jackknife replicate variance estimators (statistical packages such as STATA and SAS Version 9.2 allow for easy computation of replicate variance estimates). The development of replicate weights will facilitate the computation of standard errors for the complex analyses necessary for this survey. The replicates will be based fundamentally on the first-phase district sample (so that each replicate is associated with one set of ‘dropped’ districts), but the school weights will need to be carefully calibrated to provide school-level replicate weights that correctly reflect the effects of the balanced sampling process (the replicate weights are recalibrated to add to the stratum totals). We anticipate nonresponse, which we will adjust for by utilizing information about the nonresponding districts and schools from the frame and other sources regarding funding and other important district and school characteristics. This information will be used to generate nonresponse cells with differential response rates. The nonresponse adjustments will be equal to the inverse of the weighted response rate. This will adjust for bias from nonresponse.

B.4 Test of Procedures

The state survey will be pre-tested with nine or fewer state officials. The school district survey and the poll will be pre-tested with nine or fewer district officials. The school survey will be pre-tested with nine or fewer school officials.

B.5 Individuals Consulted on Statistical Aspects of Design

The statistical aspects of the design have been reviewed by staff at the Institute of Education Sciences. The individuals most closely involved in developing the statistical procedures include:

Marsha Silverberg, IES, Project Officer, 202-208-7178

Meredith Bachman, IES, 202-219-2014

Babette Gutmann, Westat, project director, 301-738-3626

Patty Troppe, Westat, deputy project director, 301-294-3924

Lou Rizzo, Westat, senior statistician, 301-294-4486

Juanita Lucas-McLean, director of data collection, 301-294-2866

Bruce Haslam, Policy Studies Associates, director of design, 202-939-5333

Michael Puma, Chesapeake Research Associates, director of analysis, 410-897-4968

Sharon Lohr, Arizona State University, member of Technical Working Group, 480-965-4440

Thomas Cook, Northwestern University, member of Technical Working Group, 847-491-3776

1 The degree to which the State Fiscal Stabilization Fund and bolstering of already established programs (e.g., IDEA) successfully saved and created new education jobs is of policy interest as well. However, (a) this topic has been examined in other forums and (b) at the time when this study is fielded, funds tied to job retention and creation are unlikely to still be available to states, districts, and schools.

2 If additional evaluation resources are available, IES may consider an additional round of data collection in 2014 to more fully capture how implementation efforts change after ARRA funds are spent down.

3 The cutoff 40 percent is chosen as being close to a median breakpoint: roughly 50 percent of the students are in districts with less than or equal to 40 percent with free or reduced lunch, and roughly 50 percent of the students are in districts with greater than 40 percent free or reduced lunch.

4 The effective sample size is the sample size of a simple random sample with the same precision as the designated design. The design effect is the increase in variance from a simple random sample with the same sample size.

5 This sorts within each higher-level stratum as lowest to highest, highest to lowest, lowest to highest, etc. The intention is to spread the distribution across the sort as much as possible when a systematic sort is carried out.

6 Deville, J.-C., and Tillé, Y. (2004). Efficient balanced sampling: The cube method. Biometrika 91, 4, 893-912.

7 This is sqrt (P₀*(1-P₀)*((1/n₁)+(1/n₂))), where P₀ is the null population percentage, n₁ is the effective sample size in non RTT states, and n₂ is the effective sample size in RTT states.

8 The standard error of the difference under the alternative hypothesis is sqrt ((P₁*(1-P₁)/n₁)+ (P₂*(1-P₂)/n₂)), where P₁ is the non RTT population percentage, n₁ is the sample size in non RTT states, P₂ is the RTT population percentage, and n₂ is the sample size in RTT states.

File Type	application/vnd.openxmlformats-officedocument.wordprocessingml.document
File Title	Abt Double-Sided Body Template
Author	Abt Associates Inc
File Modified	0000-00-00
File Created	2021-02-01