SES-OMB Part B 4 June09
SES-OMB Part B 4 June09.doc
Feasibility and Conduct of an Impact Evaluation of Title I Supplemental Education Services
OMB: 1850-0858
Contract No.: ED-01-CO-0038-0009

Feasibility and Conduct of an Impact Evaluation of Title I Supplemental Educational Services:
Revision to Currently Approved Collection (ICR Reference Number 200805-1850-003)
Part B: Supporting Statement for Request for OMB Approval of Collection of Information Employing Statistical Methods
Submitted to:
Institute of Education Sciences U.S. Department of Education 80 F Street, NW Washington, DC 20208
Project Officer:
|
Submitted by:
Mathematica Policy Research, Inc. P.O. Box 2393 Princeton, NJ 08543-2393 Telephone: (609) 799-3535 Facsimile: (609) 799-0005
Project Director: |
CONTENTS
Page
B. COLLECTION OF INFORMATION EMPLOYING STATISTICAL METHODS 1
1. Respondent Universe and Sampling Methods 2
2. Statistical Methods for Sample Selection and Degree of Accuracy Needed 3
3. Methods to Maximize Response Rates and Deal with Nonresponse 11
4. Tests of Procedures and Methods to be Undertaken 11
5. Individuals Consulted on Statistical Aspects of the Design 13
REFERENCES 14
B. COLLECTION OF INFORMATION EMPLOYING STATISTICAL METHODS
This is a second-stage request for approval to carry out outcome data collection activities for the Feasibility and Conduct of an Impact Evaluation of Title I Supplemental Educational Services. During the baseline year (school year 2008-09), we were able to recruit 8 districts; however, these districts yielded fewer SES applicants than anticipated and were concentrated geographically—with a disproportionate number in a single state—and are not likely to include enough eligible SES applicants to achieve the desired sample size.1 In order to achieve the goal of 50,000 participating students and increase the geographical diversity of the sample, we will recruit a second cohort of districts during the 2009-2010 school year. The number of districts to be recruited remains the same as previously approved by OMB, totaling 12 districts. In this second clearance request, the Institute of Education Sciences (IES) of the U.S. Department of Education requests OMB approval for the outcome data collection phase, which for the original districts (cohort 1) will occur in spring 2009, and for the new districts (cohort 2) will occur in spring 2010. The data collection phase includes: (1) an SES provider survey (which will allow the contractor to assess provider characteristics that can then be linked to impacts), (2) SES student participation data, and (3) the collection of student records including state and/or district test scores, which are the main outcomes for the evaluation.
The Feasibility and Conduct of an Impact Evaluation of Title I Supplemental Education Services received OMB approval (ICR reference number 200805-1850-003, ICR tracking number 3634) on August 21, 2008. OMB approved the first clearance request describing the study, the regression discontinuity design (discussed below), and baseline data collection activities. Feasibility was determined based on the recruitment and baseline data collection efforts, and in August 2008, the Institute of Education Sciences (IES) approved the option to proceed with the conduct of the full study.
As noted in the original submission, collection of information is needed to support a rigorous evaluation of supplemental educational services (SES) for the U.S. Department of Education (ED). The No Child Left Behind Act (NCLB) requires school districts to offer SES to students who attend schools that have failed to make adequate yearly progress (AYP) for three consecutive years. SES are tutoring or other academic support services offered outside the regular school day by state-approved providers, free of charge to eligible students. Parents can choose the specific SES provider from among a list of providers approved to serve their area. This evaluation is authorized under the No Child Left Behind Act of 2001, Section 1501 (PL No 107-110).
Mathematica Policy Research (MPR) is working with ED to design and conduct a rigorous evaluation of SES based on a regression discontinuity (RD) design in up to 12 districts. The primary research questions to be answered by the evaluation are: (1) what is the effect of SES on student achievement? and (2) how does the effect of SES vary by student and provider characteristics? MPR will assess the impact of SES by comparing a treatment and control group of students, where the treatment and control groups are formed purposefully based on a measure of prior achievement (such as a test score or grade point average). Valid estimates of the effect of SES can be determined by comparing the average reading and math scores of students who were accepted into SES to the average scores of students who were not accepted into SES, after regression adjusting for the measure of prior achievement used to determine acceptance (this is the definition of an RD design). MPR will assess how impacts vary by provider characteristics by calculating provider-specific impacts and then relating those impacts to provider characteristics, as measured using a survey of SES providers.
1. Respondent Universe and Sampling Methods
School districts, students, and SES providers are the primary units of data collection and analysis for the full evaluation. During the design phase, ED’s Office of Innovation and Improvement (OII) compiled a list of 24 school districts that were oversubscribed for SES during the 2007-2008 school year and likely to be oversubscribed during the 2008-2009 school year. In fall 2008, OII provided the names of other districts potentially oversubscribed for the 2008-09 school year, to contact for possible inclusion as a second cohort in the study. The recruited districts, including the additional potential ones to be contacted and possibly recruited starting this fall, are listed in Table B.1. Under the original OMB clearance and as part of the first year design and feasibility study, we assessed the feasibility of conducting the evaluation through informal conversations with district officials in 9 of these districts. During the recruitment and baseline data collection, the contractor was able to determine that there was sufficient number of districts with oversubscription that allocated services based on quantifiable measures of prior student achievement (or similar assignment variables), that it is possible to evaluate SES using an RD design.
TABLE B.1
RECRUITED SCHOOL DISTRICTS AND POTENTIAL DISTRICTS FROM WHICH ADDITIONAL SAMPLE WILL BE RECRUITED
Recruited School District Name (Cohort 1) |
State |
Albuquerque Public Schools |
New Mexico |
Bridgeport School District |
Connecticut |
Cincinnati School District |
Ohio |
Collier County School District |
Florida |
Dade County School District |
Florida |
Gadsden County School District |
Florida |
Palm Beach County School District |
Florida |
Pinellas County School District |
Florida |
Potential Districts Added Fall 2009 (Cohort 2) |
|
Akron City School District |
Ohio |
Anchorage School District |
Alaska |
Boston Public School District |
Massachusetts |
Fall River Public School District |
Massachusetts |
Hartford School District |
Connecticut |
Long Beach Unified School District |
California |
Malden Public School District |
Massachusetts |
Pomona Unified School District |
California |
Providence School District |
Rhode Island |
San Diego Unified School District |
California |
From each district we will potentially include all eligible SES applicants at the relevant grade levels in the impact analysis2 and will include all SES providers in the provider survey (see Table B.2). Based on prior studies, we anticipate a response rate of at least 80 percent to the SES provider survey, and anticipate that test score data from administrative records will be available for all the students, for a potential total sample of 50,000 students from both cohorts.
Determining Eligibility. School districts are eligible for the evaluation if (1) they have more applicants for SES than can be served with available funds and (2) they accept applicants based on a quantifiable, continuous measure of prior achievement (such as test score or grade point average). At this point, 8 districts identified by OII meet the eligibility criteria and have agreed to participate in the study. The contractor is ascertaining the suitability and interest of the 10 new districts identified as potential sites in hopes of adding a second cohort thereby increasing the overall sample up to 12 districts.
TABLE B.2
SAMPLE SUMMARY
Unit of Data Collection/Analysis |
Number Provided by OII |
Number Expected for Study |
Anticipated Response Rate |
School district (cohort 1) |
24 |
8 |
Not Applicable |
School district (cohort 2) |
10 |
4 |
Not Applicable |
|
|
|
|
SES provider (cohort 1) |
480 estimateda |
384 |
> 80% |
SES provider (cohort 2) |
83 estimateda |
66 |
>80% |
a Based on the number of providers approved to give services within our participating districts we expect approximately 384 SES providers in cohort 1, and have estimated that there will be an additional 83 providers from the potential districts still under consideration (cohort 2).
2. Statistical Methods for Sample Selection and Degree of Accuracy Needed
Our goal is to include up to 12 districts and a minimum sample size of 50,000 students in the impact evaluation. This sample should allow us to detect impacts of 0.20 standard deviations with high probability for specific subgroups of SES providers. Power calculations and other details are shown below. For clarity, we have left some language from the original, cleared OMB submission to provide OMB with an overview of the entire design and analysis plan.
a. Statistical Methodology for Stratification and Sample Selection
We will not draw a random sample of service providers or students. We do not expect to have the opportunity to randomly sample districts, because the total number of oversubscribed districts nationally is very small, and we are seeking to include all of them.
b. Estimation Procedures
A randomized experimental evaluation of SES is precluded by NCLB, which requires that all eligible students who request services receive them, as long as resources are available. Although a randomized design is precluded by statute, NCLB’s rules about the allocation of services when resources are constrained create the opportunity for an RD analysis that will allow causal inferences with rigor approaching that of a randomized experiment.
Impacts will be estimated in a manner consistent with the study’s RD design. Using an RD design, valid estimates of the effect of SES can be determined by comparing the average reading and math scores of students who were accepted into SES to the average scores of students who were not accepted into SES, after regression adjusting for the measure of prior achievement used to determine acceptance. Figure B.1 illustrates the RD design graphically, using a hypothetical example in a hypothetical district. Measures such as prior test scores or grade point average could be used for assignment to treatment or control groups. In this example, students with an assignment score of 50 or less receive SES (the treatment group), and students with a score over 50 do not (the control group). This figure plots student math test scores against assignment scores. It also displays the fitted regression line for the treatment and comparison groups. The estimated impact on math test scores is the vertical distance between the two regression lines at the cutoff value of 50. An important consideration in calculating impacts using an RD design is the functional form used to regression adjust for prior achievement. In Figure B.1, the functional form is linear. In practice we will also calculate impacts using non-parametric regression techniques that allow for a more flexible functional form.
Figure B.1
HYPOTHETICAL EXAMPLE OF THE RD METHOD
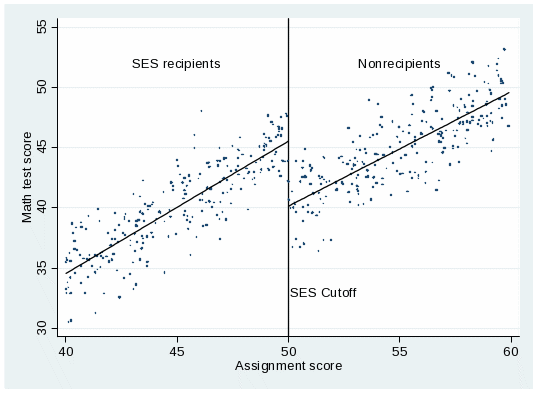
Because the assignment score will be defined differently across districts (we anticipate that in most cases it will be based on a prior year’s test score) and because each district will use a different cutoff for allocating services, we will estimate separate impacts for each district in the sample and then compute a weighted average of these estimates to obtain an overall estimate of the impact of SES among the districts in our sample.3 We will weight district-specific estimates according to the number of eligible students in each district, which will provide an estimate of the impact of SES on the average student under study.
Using survey data from SES providers (as requested in this revised OMB package) we will explore the relationship between SES provider characteristics and RD estimates of impacts. As part of the district SES application materials, parents are typically asked to identify up to three preferred SES providers. Because the preferred providers will be identified prior to determining the RD cutoff, we will be able to calculate provider-specific impacts for districts served by the largest providers.4 However, very few providers will have a large enough sample size for sufficient statistical power to produce reliable provider-specific estimates. In most cases, provider-specific estimates will be aggregated across providers based on provider characteristics and practices.” Dimensions along which interventions might vary include substantive focus (for example, math or reading), intensity (for example, frequency of student attendance), and method of delivery (for example, small group activities, one-on-one tutoring, or the use of computer technology).
One additional consideration is that some students offered SES might not receive the services, and some students whose assignment score exceeds the cutoff might nonetheless manage to receive SES.5 If this is the case, the impact estimates will represent the impact of offering students SES rather than the effect of receiving SES. We will be collecting data on whether students received SES from the SES provider survey and from district administrative records. If many students who were offered SES chose not to receive them, or if students who should not have received SES according to their assignment score do in fact receive them, we can compute an additional estimate reflecting the impact on students of receiving SES, using what is known as a “fuzzy” RD design (Trochim 1984; Hahn et al. 2001). This approach is similar to calculating the impact of treatment on the treated in a randomized control trial using a Bloom (1984) adjustment, essentially using the discontinuity in SES receipt at the assignment score cutoff as an instrumental variable for SES receipt, holding constant a function of the assignment score.
c. Degree of Accuracy Needed
An important distinction between an evaluation of SES and many other evaluations of education interventions is that SES are not a single intervention. Instead, they provide the parents of low-income, low-achieving students with the opportunity to enroll their children in an intervention of their choosing among a variety of programs within a range constrained by NCLB and the state approval process. Consequently, the effects of specific types of interventions funded by SES may be of as much interest to parents and policymakers as the overall effect of SES.
Our goal is for the study to be able to detect, with high probability, an impact of 0.20 standard deviations for subgroups of students corresponding to specific types of services. Dimensions along which interventions might vary include substantive focus (for example, math or reading), intensity (for example, frequency of student attendance), and method of delivery (for example, small group activities, one-on-one tutoring, or the use of computer technology). Many evaluations of education interventions are designed to detect effects on academic achievement of at least 0.20 standard deviations with high probability. For example, the contractor (MPR)’s evaluation of math curricula and the evaluation of reading comprehension interventions are designed to detect effects in the range of 0.20 and 0.25 standard deviations. By designing the study to detect moderate effects of specific intervention types, we will also be able to detect very small effects of SES overall. The RAND study of SES (Zimmer et al. 2007) found overall average effects in some school districts of less than 0.10. Our study will most likely be able to detect effects smaller than 0.10 for the full sample, as we show below.
The MDE for an RD Design
The minimum detectable effect (MDE) for an RD design is different from the MDE for a random assignment design because of the correlation between treatment status and the score used to define the cutoff, which in turn determines treatment status. We can obtain the impact estimate on an outcome, y, by using the following equation:
(1) ![]()
where T is the treatment indicator variable, Score is the score used to assign the units to the treatment or comparison groups, and u is a random error term. In this equation, the impact is identified by assuming that the relationship between y and Score (that is, β2) is the same for the treatment and comparison groups and that the functional form specifying this relationship is linear. The intercepts of the fitted lines, however, are allowed to differ by research status. Thus, the impact estimate is β1 and represents the difference between the intercepts of the fitted lines for the treatment and comparison groups. Stated differently, the impact is the difference between the two fitted lines at the point of “discontinuity” (that is, at the threshold score value in the y-Score plane).
To calculate an MDE, we need to know the variance of 1. Because of the high correlation between 1 and 2, the variance of 1 is greater than in the case of a randomized controlled trial (RCT). The ratio of the variance of 1 in an RD design to the variance of 1 in an RCT is the RD “design effect,” represented mathematically as
(2) ![]()
where
![]() is the regression R2 value from equation (2),
is the regression R2 value from equation (2),
![]() is the regression R2 value under an experimental design,
and
is the regression R2 value under an experimental design,
and
![]() is the R2 value when T is regressed on Score
(and an intercept). The first ratio in the design effect is
essentially 1, because the same explanatory variables would be used
in either an RD or a random assignment design. The second ratio is
what drives the design effect. This ratio could also be expressed in
terms of the correlation between T and Score—the
greater that correlation, the greater the design effect.
is the R2 value when T is regressed on Score
(and an intercept). The first ratio in the design effect is
essentially 1, because the same explanatory variables would be used
in either an RD or a random assignment design. The second ratio is
what drives the design effect. This ratio could also be expressed in
terms of the correlation between T and Score—the
greater that correlation, the greater the design effect.
The correlation between T and Score depends on two things: (1) the relative proportion of individuals in the treatment and control groups and (2) the distribution of the Score variable. In Table B.3, we examine how the design effect varies with respect to these two factors. The design effects are calculated using computer simulations.
TABLE B.3
REGRESSION DISCONTINUITY DESIGN EFFECTS
|
Probability Distribution of Score |
|
Proportion of Students in Treatment/Control Groups |
Normal |
Uniform |
90:10 |
1.5 |
1.4 |
80:20 |
1.9 |
1.9 |
70:30 |
2.4 |
2.8 |
50:50 |
2.8 |
4.0 |
The MDE of an RD design is found by multiplying the MDE of an RCT (with the same sample size) by the square root of the RD design effect. For example, if the MDE for an RCT is 0.20 and the RD design effect is 1.5, then the MDE for an RD study with the same sample size as the RCT will be 0.24.
Relationship Between the MDE and Key Design Parameters
The MDE depends on the following key design parameters:
The Number of Students in the Study. As with RCTs, including more students in the study increases the precision of impact estimates and reduces the study’s MDE.
The Distribution of the Cutoff Score. As described in the previous section, the distribution of the cutoff score influences the correlation between the score and the treatment variable. The greater that correlation, the greater the RD design effect. Because the cutoff score is likely to be a measure of prior achievement, we assume in all calculations presented below that the cutoff score follows the normal distribution.
The Proportion of Students That Falls Below the Cutoff to Receive Services. As with RCTs, an RD design will have greater statistical power if the number of students assigned to treatment is the same as the number assigned to the control condition. Because demand for SES has only recently begun to outpace funding, we anticipate that the proportion of students that falls below the cutoff to receive services will be high, which means that there will be many more in the treatment than in the control condition. We assume that the size of the control group will not exceed 20 percent of the total sample.
The Difference Between the Treatment and Control Groups in the Proportion of Students That Actually Participates in SES. Some students who are offered SES (those below the RD cutoff) might not actually enroll, which means that the proportion of students that participates in SES in the treatment group may be less than 1. At the same time, we anticipate that districts will allow some students above the cutoff to participate in SES in order to “fill the slots” left open by those who were offered SES but declined the offer. This is conceptually similar to the problem of noncompliance in RCTs, and the same correction can be used in an RD design as is used in an RCT. We assume that the difference in participation rates could be as low as 50 percent (for example, an 80 percent participation rate below the cutoff and a 30 percent participation rate above it).
The clustering of students within districts is not listed as a design parameter because we will treat district effects as fixed, not random. That is, districts are not the unit of assignment and they are not a unit of random sampling. Therefore, they do not contribute variance to the impact estimate. Clustering of students within schools or classrooms is also not an issue, because we are not sampling schools or classrooms (we are including all students who apply to SES in the study districts). In Table B.4, we show MDEs for a range of sample sizes, proportions of students in the treatment and control groups, and differences in the participation rates between the treatment and control groups, holding the regression R2 fixed at 0.40.6 This table shows that for a subgroup of 5,000 students,7 the study will have an MDE of less than 0.20 as long as the proportion of students in the control group is 10 percent or higher and the difference in participation rates between the treatment and control groups is at least 65 percent. If the proportion of students in the control group falls to 5 percent, then a difference in participation rates of 80 percent would be needed in order to attain an MDE of 0.20 for a subgroup of 5,000 students. With a subgroup of 2,500 students, the study would need a difference in participation rates of nearly 80 percent and 20 percent of students in the control group to attain an MDE of 0.20 standard deviations.
TABLE B.4
VARIATION
IN MINIMUM DETECTABLE EFFECT SIZES WITH RESPECT TO TAKE-UP RATES
AND
THE PROPORTION OF STUDENTS IN THE TREATMENT/CONTROL GROUPS
|
|
Difference in the Participation Rate Between the Treatment and Control Group |
||
SES Applicants |
Control Group Size |
80 Percent |
65 Percent |
50 Percent |
5 Percent of Students in the Control Group |
||||
50,000 |
2,500 |
0.06 |
0.08 |
0.10 |
25,000 |
1,250 |
0.09 |
0.11 |
0.14 |
10,000 |
500 |
0.14 |
0.17 |
0.23 |
5,000 |
250 |
0.20 |
0.25 |
0.32 |
2,500 |
125 |
0.28 |
0.35 |
0.45 |
10 Percent of Students in the Control Group |
||||
50,000 |
5,000 |
0.05 |
0.06 |
0.08 |
25,000 |
2,500 |
0.07 |
0.09 |
0.11 |
10,000 |
1,000 |
0.11 |
0.14 |
0.18 |
5,000 |
500 |
0.16 |
0.19 |
0.25 |
2,500 |
250 |
0.22 |
0.27 |
0.36 |
20 Percent of Students in the Control Group |
||||
50,000 |
10,000 |
0.04 |
0.05 |
0.07 |
25,000 |
5,000 |
0.06 |
0.07 |
0.10 |
10,000 |
2,000 |
0.09 |
0.12 |
0.15 |
5,000 |
1,000 |
0.13 |
0.17 |
0.21 |
2,500 |
500 |
0.19 |
0.23 |
0.30 |
N ote:
The MDEs are expressed in effect size units and were calculated
assuming (1) a 2-tailed test; (2) a 5 percent significance level α;
(3) an 80 percent level of power β;
(4) a reduction in variance of 40 percent owing to the use of
regression models to estimate impacts, R2;
and (5) an RD score variable that follows the normal distribution.
The figures were calculated using the following formula:
ote:
The MDEs are expressed in effect size units and were calculated
assuming (1) a 2-tailed test; (2) a 5 percent significance level α;
(3) an 80 percent level of power β;
(4) a reduction in variance of 40 percent owing to the use of
regression models to estimate impacts, R2;
and (5) an RD score variable that follows the normal distribution.
The figures were calculated using the following formula:
where fct is the sum of two critical values (corresponding to α and β) from the T-distribution with df degrees of freedom, RD is the regression discontinuity design effect, PR is the difference in participation rates between students below and above the RD cutoff, PSC is the proportion of students in the control group, PDF is the probability density function of the score used to determine participation in the RD design (assumed normal), NT is the number of students in the treatment group, and NC is the number of students in the control group.
Based on these calculations, our goal is to recruit enough districts into the study to provide a student sample of at least 50,000. If we are able to include only districts that appear likely to have an oversubscription rate of at least 10 percent, then it is likely that we will be able to detect an MDE of 0.20 for a subgroup of 5,000 students.
d. Unusual Problems Requiring Specialized Sampling Procedures
We do not anticipate any unusual problems that require specialized sampling procedures.
e. Use of Periodic Data Collection Cycles to Reduce Burden
The data collection plan calls for the minimum amount of data needed to measure differences in student achievement based on SES provider. The collection of SES provider data and student achievement test scores will be one-time collections.
3. Methods to Maximize Response Rates and Deal with Nonresponse
In order to maximize the response rates for the Provider Survey, we plan on sending providers an initial packet which will include both a letter from ED as well as a letter from the district detailing the importance of the study and encouraging participation. Approximately 10 days later, a second follow up packet will be sent to non-responders. Approximately 10 days after the second mailing, telephone interviewers will begin calling non-responding providers and encouraging them to complete the survey by telephone. In addition, email reminders will also be a part of the contact strategy. A toll-free line will be available for sample members to call if they have any questions about the study and their participation. All telephone interviewers will be trained to answer any questions about the study to help alleviate concerns respondents may have. We feel confident that with these strategies along with the proposed $30 incentive we will attain an adequate response rate of at least 80%.
For the districts and the data collection of school records and participation data, we expect 100 percent cooperation, as we have successfully been working with each district throughout the recruiting and baseline data collection phases. Before agreeing to be part of the study, each district indicated that the data needed for the study was available and that they were willing to share it with the contractor. The contractor will assist each district to minimize the burden related to gathering and sending the information and will accommodate whatever format is easiest for the districts.
4. Tests of Procedures and Methods to be Undertaken
To help ED address the study research questions, the contractor will collect and analyze data from several sources. Clearance has already been given for the design and baseline data collection of SES application data.
The current revised request is to collect outcome data, including: (1) an SES provider survey (which will allow the contractor to assess provider characteristics that can then be linked to impacts), (2) SES student participation data, and (3) the collection of student records, including state and/or district test scores (the main outcome for the evaluation). Table B.5 shows the schedule of these data collection activities (including previously approved baseline data collection activities).
TABLE B.5
DATA
COLLECTION SCHEDULE
Activity |
Respondent |
Clearance Previously Approved |
Clearance Requested in Current Package |
Baseline Data Collection, Fall 2008: Collect SES application data (35,000 records from 8 districts – cohort 1) |
Parent/guardian via school districts |
X
|
|
Outcome Data Collection, Spring 2009: SES provider survey – cohort 1 (384 providers) |
SES provider |
|
X |
Outcome Data Collection, Spring/Summer 2009: Obtain SES student participation data from district (35,000 – cohort 1) |
District/School staff/ SES Providers |
|
X |
Outcome Data Collection, Summer 2009: Obtain student records/district test scores – cohort 1 (55,000 records) |
District/School staff |
|
X |
Additional Baseline Data Collection, Fall 2009: Collect SES application data from up to 4 additional districts – cohort 2 (15,000 records) |
Parent/guardian via school districts
|
X |
|
Outcome Data Collection, Spring 2010: SES provider survey - cohort 2 (66 providers) |
SES provider |
|
X |
Outcome Data Collection, Spring/Summer 2010: Obtain SES student participation data from district (15,000 – cohort 2) |
District/School staff/ SES Providers |
|
X |
Outcome Data Collection, Summer 2010: Obtain student records/district test scores - cohort 2 (15,000 records) |
District/School staff |
|
X |
SES Provider Survey
In spring 2009, the contractor will collect information from SES providers (cohort 1 providers) through a self-administered questionnaire. The questionnaire (a mail survey with telephone followup) will focus on provider characteristics (for example, type and size of organization, years in existence); staff characteristics (gender, ethnicity, prior teaching experience, current certification, employment in study district); services provided (type, frequency, delivery methods); and characteristics of all the students they serve, not just those in the study. The contractor pre-tested the instrument during the winter of 2009 and confirmed that on average, the instrument took 30 minutes to complete. This included the time respondents needed to look up information. Issues with the overall questionnaire design, question wording, and question order have all been addressed and the changes are reflected in the final version of the questionnaire (attached). Copies of the Provider Survey and an example of accompanying letters are included in Appendix A
SES Student Participation Data
A second source of information about services will be obtained through gathering SES student participation data including information on the type and amount of services provided to each student served in the 2008-2009 school year (or 2009-2010 for cohort 2). We plan to gather the student participation data from districts and have confirmed during our baseline data collection efforts that the districts can provide sufficiently detailed attendance information needed for the study. The SES attendance and participation information will be requested during the school records data collection effort although the information may be kept in different systems at the district. A copy of the student participation spreadsheet is included in Appendix B.
Collection of Demographic Data and Student Achievement Scores
During the summer/early fall of 2009, the contractor will collect scores from tests administered by the state or district in school years 2006–2007, 2007–2008, and 2008–2009. The demographic and other student-level information we will collect from the districts includes grade level, month and year of birth, race/ethnicity, English proficiency, disability status, eligibility for free or reduced-price school lunch, student grades, and school attendance. We will also ask the district to provide SES attendance information on each SES participant, if available. We anticipate that we will be able to obtain school records for 35,000 students across the 8 original cohort 1 districts. The same information will be requested from the four cohort 2 districts for the estimated 15,000 2009-2010 SES applicants in the summer/early fall of 2010 (school years 2007–2008, 2008–2009, and 2009-2010 for 2009-10 SES applicants).
5. Individuals Consulted on Statistical Aspects of the Design
This study is being conducted by contractor, Mathematica Policy Research, Inc. (MPR), under contract to the U.S. Department of Education. The project director is Dr. Brian Gill, the principal investigator is Dr. John Deke, and the survey director is Ms. Laura Kalb—all MPR employees. The project team consulted with Dr. Peter Schochet, senior researcher at MPR, about the statistical aspects of the study design. Contact information is provided below.
Brian Gill, Mathematica Policy Research, Inc. 617-301-8962
John Deke, Mathematica Policy Research, Inc. 609-275-2230
Laura Kalb, Mathematica Policy Research, Inc. 617-301-8989
Peter Schochet, Mathematica Policy Research, Inc. 609-936-2783
REFERENCES
Bloom, H.S. “Accounting for No-Shows in Experimental Evaluation Designs.” Evaluation Review, vol. 8, 1984, pp. 225-246.
Hahn, Jinyong, Petra Todd, and Wilbert Van der Klaauw. “Identification and Estimation of Treatment Effects with a Regression-Discontinuity Design.” Econometrica, vol. 69, no. 1, January 2001.
Shadish, W.R., Thomas D. Cook, and Donald T. Campbell. Experimental and Quasi-Experimental Designs for Generalized Causal Inference. Boston: Houghton Mifflin, 2002.
Trochim, W. Research Design for Program Evaluation: the Regression-Discontinuity Approach. Beverly Hills: Sage Publications, 1984.
Zimmer, Ron, Brian Gill, Paula Razquin, Kevin Booker, and J.R. Lockwood III. State and Local Implementation of the No Child Left Behind Act. Volume I: Title I School Choice, Supplemental Educational Services, and Student Achievement. Washington, DC: U.S. Department of Education, 2007.
1 The eight districts have a total of approximately 55,000 eligible SES applicants in 2008-09, with approximately 80% of the sample from Florida.
2 We expect that the number of those that can ultimately be included in the analytic sample will be substantially smaller, for several reasons. Some of the districts have stratified prioritization schemes that will rule some students out of the analysis; some of the districts may not be able to provide outcome data on all of the students; and the analysis is likely to include a “bandwidth” restriction that excludes applicants with very high and very low scores.
3 In some districts, assignment score and/or cutoff might also differ by grade, in which case we will estimate district/grade-specific impacts.
4 Provider specific impacts will be calculated by comparing the outcomes of students in the treatment group who identified a given provider as their preferred provider to the outcomes of students in the control group who identified the same provider as their preferred provider. By identifying the preferred provider during the application process, we will be able to know which students to include in the control group for this analysis (otherwise, we would not know who to compare the treatment group to).
5 This second concern is known as comparison group “crossover,” which might occur if the district erroneously provides the student SES or does not have a systematic approach for allocating available services from a waiting list when students initially offered SES decline them.
6 We typically assume a regression R2 of 0.50 in cases where a baseline test score is available as a covariate. In this study, a baseline test score will be available in most cases and used as the basis for the RD design. However, because we anticipate that some students in our sample will lack a baseline test score, we assume an overall regression R2 of 0.40 instead of 0.50. These students can still be included in the study if another measure of prior achievement, such as grade point average, is available. But those other measures may not be as highly correlated with the follow-up test score as a baseline test score would have been, hence the lower R2 assumption.
7 With a total sample of 50,000 students, we would be able to analyze 10 subgroups of this size that would correspond to different types of services.
| File Type | application/msword |
| File Title | MEMORANDUM |
| Author | Darlene Hrbek |
| Last Modified By | Yumiko Sekino |
| File Modified | 2009-06-04 |
| File Created | 2009-06-04 |
© 2026 OMB.report | Privacy Policy