Att_REL West ENAS_OMB Supporting Statement Part B_08.13.07
Att_REL West ENAS_OMB Supporting Statement Part B_08.13.07.doc
REL West Educational Needs Assessment Survey
OMB: 1850-0853
REL West Educational Needs Assessment Survey
(Task 1.1)
Request for OMB Approval
Supporting Statement for Paperwork Reduction Act Submission
Part B
Version 3
Revised Submission: August 2007
Submitted to: Submitted by:
U.S. Department of Education Regional Educational Laboratory West
Institute of Education Sciences (REL West at WestEd)
555 New Jersey Ave., NW, Rm. 308 730 Harrison Street
Washington, DC 20208 San Francisco, CA 94107
(202) 208-7078 (415) 615-565-3000
Project Officer: Project Director:
Rafael Valdivieso, Ph.D. Hans Bos, Ph.D.
U.S. Department of Education Berkeley Policy Associates (BPA)
(202) 208-0662 (510) 465-7884 x 217
TABLE OF CONTENTS
Supporting Statement B: Data Collection Procedures and Statistical Methods
B-1. Respondent Universe and Sampling Methods……………………………………………….. |
1 33 |
B-2. Statistical Power of the Sample………………………………………………………………. |
5 |
B-3. Maximizing Response Rates……..……………….………………………………………….. |
7 |
B-4. Pretesting of Surveys……………………………………………………………………….…. |
8 |
B-5. Contact Information……..……………………………………………………………………… |
8 5 |
References for Part B………………………………………………………………………………… |
9 |
|
|
Appendices |
|
Appendix A. Teacher Survey |
|
Appendix B. School Administrator Survey |
|
Appendix C. District Administrator Survey |
|
Appendix D. California County Superintendent Survey |
|
Appendix E. Mail/Email Letter |
|
Appendix F. Federal Register Notice |
|
Appendix G. Confidentiality Agreements |
|
|
|
REL West Educational Needs Assessment Survey
SUPPORTING STATEMENT PART B:
Collections of Information Employing Statistical Methods
B1. Respondent Universe and Sampling Methods
Respondent Universe/Population
The survey is designed to assess the educational research and development needs in the four-state region covered by the REL West. This includes Arizona, California, Nevada, and Utah. Within this region, the survey assesses needs as experienced by three distinct groups of educators: teachers, school administrators, and district administrators. In addition the survey will be administered to all 58 California County Office of Education (COE) superintendents. This is the case only for California because of the special role COEs play in this large and populous state, with County staff having similar responsibilities in relation to the districts they serve as district staff have in relation to the schools they serve. In addition, when consulted about this project’s scope and purpose, the Association of COEs (CCSESA, or the California County Superintendents Educational Services Association) expressed interest in having their members participate in the survey.
Slightly different versions of the survey will be administered to these four groups (See Appendices A–D).1 This survey is designed in such a way that results may be combined for certain analyses, but the sample is designed to produce reliable survey results for each of the four main constituent groups separately as well as for each of the four states.
Specifically, the population includes the following groups:
Classroom teachers represent the largest group. It includes teachers in PK-12 classrooms in public schools across the four states. The population includes both regular classroom teachers and special education teachers and covers the full range of subjects and school levels (e.g., elementary, secondary). Across the four states, there are approximately 398,141 teachers, 305,969 of whom work in California, 48,935 in Arizona, 20,950 in Nevada, and 22,287 in Utah. The distribution across school level is as follows: 69 percent teach in elementary schools,2 28 percent in secondary schools, and 3 percent in ungraded schools.3
The second largest group is school administrators. Across the four states there are approximately 17,959 school administrators, 13,752 of whom work in California, 2,223 in Arizona, 924 in Nevada, and 1,060 in Utah.4
The third group is school district administrators. Across the four states there are approximately 1,531 school district superintendents, 1,056 of whom work in California, 418 in Arizona, 40 in Nevada, and 17 in Utah.5
The final group is particular to California. The superintendent from each of the 58 County Offices of Education will be surveyed due to their unique responsibilities in California in directly supporting schools and districts to improve student achievement.
Exhibit 1. Estimates of the respondent universe, sample, and expected respondents by respondent type and state
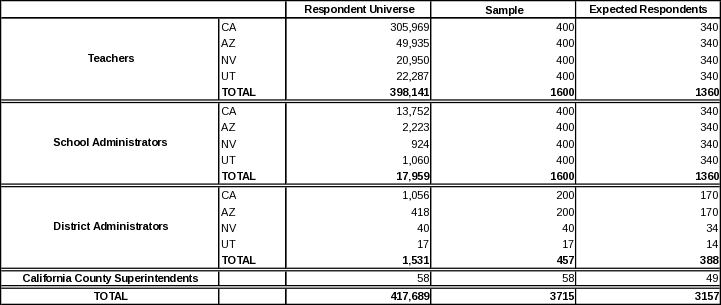
We determined that the most cost effective sample size would be no greater than 4,000 potential respondents for this study. More about our methods for collecting data and maximizing response rates is included in Section B3.
The overall response rate is expected to be 85. Web-based and email survey administrations usually obtain low response rates. One can expect between a 25 and 30 percent response rate from an email survey when no follow-up takes place and only slightly higher response rates when follow-up does take place (e.g., Kittleson, 1997; Mertler, 2003). More information on our response rates is also included in Section B3.
Sample Design and Selection
Sampling Strategy
To obtain a representative sample of survey respondents from each of the three main constituent populations described above (excluding CA county administrators, as we are surveying the total population), we will use membership records from the following organizations:
Teacher organizations: Arizona Education Association (AEA), California Teachers Association (CTA), California Federation of Teachers (CFT), Nevada State Education Association (NSEA), Utah Education Association (UEA)
Administrator organizations: Arizona School Administrators (ASA), Association of California School Administrators (ACSA), Nevada Association of School Administrators (NASA), Utah Association of Elementary School Principals (UAESP), Utah Association of Secondary School Principals (UASSP), Utah School Superintendents Association (USSA)
We are pursuing a partnership with each of these organizations to facilitate this survey effort. As part of this collaboration, the organizations will provide contact information for their membership to BPA for the purpose of this survey, or will send our survey to a sample of their membership according to our specifications. Together, these organizations include the majority of their respective constituent groups among their members. For example, there are approximately 48,935 teachers in Arizona and the AEA has 33,000 members. In California, there are 305,969 teachers and the CTA has 340,000 members (they also represent teachers’ aides and retired teachers, but the large majority are current teachers).6 In Nevada, there are 20,950 teachers and the NSEA has 26,000 members (they also represent other school staff in addition to teachers). In Utah there are 22,287 teachers and the UEA has 18,000 members.
Not much is known about which teachers, administrators, and school board members decide to become members of the organizations that represent them and who does not. Because of this, it is difficult to predict in what way our proposed sampling strategy will misrepresent the underlying population as a result of this selection process. However, given that these organizations represent the large majority of the individuals in their constituencies, it is unlikely that the resulting bias will be large.7
In addition to contact information, the membership information we will receive from these professional organizations will include a few basic background characteristics that will allow us to create sampling strata.8 For teachers, we will collect information about the grades they teach (if available). In addition, we will use geographic information (zip codes from school or home addresses, whichever the associations are able to provide to us, preferably from school/district addresses) as a way to approximate urbanicity and form geographic areas from which to sample. This will enable us to ensure that low-density parts of the four states (such as northern California or rural Nevada) are properly represented in the survey sample. At this point, we do not expect to oversample any specific groups of teachers. However, we may revisit this decision if we discover, after receiving the lists from the associations, that a particular group of teachers, school administrators, school district administrators, or school board members is too small to allow for subgroup analyses that we deem to be important (e.g., school district administrators in Nevada, or secondary school administrators in Nevada). In that case, we may decide to oversample those groups.9
The survey will rely on random sampling from the association membership lists to represent the diversity of the population described here. However, before drawing a survey sample, we plan to stratify the sampling frame by state and respondent type. Specifically, we will stratify the teacher and school administrator samples by school level (e.g., elementary or secondary), urbanicity, and geographic area. The purpose of stratification is to minimize random sampling variation in the survey sample and to increase the face validity of the survey results. Statistically, stratification is carried out by dividing the survey sampling frame into strata and then draw sample members from each strata with a probability equal to the ratio of the overall survey sample size to the sampling frame. Stratification modestly increases the statistical precision of survey estimates, especially in small samples. However, it is not possible to take into account the benefits of these gains in statistical precision at this time, because the data to construct survey strata are not yet available to us. Therefore, the results of the statistical power calculations presented in Exhibit 2 will be somewhat conservative.
We have determined that the most cost effective and timely way to identify potential survey respondents is our chosen method of sampling from professional organization lists. REL West has good working relationships with these organizations and these organizations have agreed to participate by giving us lists for sampling. The associations do represent a vast majority of the members of the role groups we are targeting. It is difficult and time-consuming to get truly complete lists of school and district staff and their contact information for four states. If we chose that strategy instead, we would have had to employ a stratified sampling strategy instead of random sampling. Other roadblocks introduced with trying to go through school, district, and state lists include a lack of email addresses in many jurisdictions, and as we explained in the Supporting Statements, we are conducting an online survey, with related communication delivered via email to cut down on time and cost needed to complete this project. Finally, engaging the associations provides an added benefit of building two-way communication between the regional lab and the many associations in the states we serve so that we may increase the probability of their suggesting research studies and our being able to effectively disseminate our study findings to them and their members. The fact that there may be a self-selection bias introduced by going through associations is balanced against the increased response rate we expect as a result of members’ associations endorsing (implicitly or explicitly) this survey.
B2. Statistical Power of the Sample
The sample composition is shown in Exhibit 2 below. A total of 3,715 potential respondents will be sampled across the four states and across the four constituent groups. Assuming a response rate of 85 percent, the expected overall respondent sample will include 3,157 individuals. Samples in individual states will be 899 in California, 850 in Arizona, 694 Utah, and 714 in Nevada. Samples of major role groups will be 1,360 teachers, 1,360 school administrators, and 388 school district superintendents. With these sample sizes, we expect to have 95 percent confidence intervals of 50 percent plus or minus 1.7 percent for the full sample; 3.3 percent for California, 3.4 percent for Arizona, 3.7 percent for Utah and Nevada; and 2.7 percent for teachers, 2.7 percent for school administrators, and 5.0 percent for school district superintendents (assuming a binomial outcome with a mean of .5).
We calculated the confidence intervals by multiplying the z-score for a 95 percent confidence interval by the standard error of the mean (the mean being 50 percent or .5). Since we are sampling a large proportion of the population of each group, in most cases (e.g., school administrators), we applied the finite population correction factor to our confidence intervals. The finite population correction factor is typically used when a survey samples all or most of the members of the population. The finite population correction factor is calculated by multiplying the standard error in the confidence interval calculation by (1-f) where f=n/N. Applying the finite population correction factor improves the confidence interval because it accounts for the fact that most of the population is being surveyed. In cases where less than 5 or 10 percent of the population is being sampled the finite population correction factor will not change or improve the confidence interval.
Confidence intervals were calculated using the following equation:
196*SQRT((.25/n)*(1-f))
Where SQRT=square root
n=expected total respondent sample
(1-f)=the finite population correction factor
f=n/N or expected total respondent sample/respondent universe
Exhibit 2. Sample composition and statistical power calculations
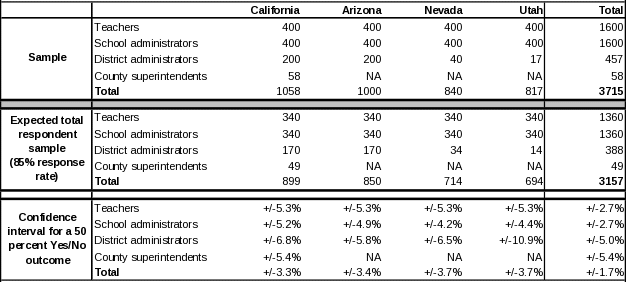
NA Not applicable.
NOTE: For California County Superintendents the entire population is being surveyed.
B3. Maximizing Response Rates
An important challenge in conducting this survey will be to obtain a sufficiently large response rate (85 percent) so that the findings will be valid and reliable. To address this challenge, we will administer the survey as follows:
1. Prior to our contacting potential respondents, the professional organizations that provide us with contact information will send their sampled members a letter (or we will send the letter) announcing the survey and explaining its importance for the field and for their membership (see Appendix E. Letter). This letter will also include information on how to access and complete the survey.
2. Using the contact information provided by the professional organizations, we will send all sample members an email (see Appendix E. Letter) with a web-link and a phone number. Sample members will be asked to complete the survey online, but will be given the opportunity to complete it by phone by calling BPA, where staff members will be ready to take their calls and will read the same introduction, instructions, and questions as those on the online version. Returned emails will be corrected and resent wherever possible. If respondents have not completed the survey within one week, a reminder email will be sent out. A reminder email will be sent out once a week until the respondent completes the survey or the end of the field period, whichever occurs first.
3. If the respondents do not respond within two weeks of receiving the first email (therefore they will have received a second, reminder email already as well), we will contact these sample members by telephone. (If the phone is not answered after a number of attempts —which is considered as a single contact — or no valid phone number is provided, we will follow up both by weekly email and by regular mail). If sample members do not have time to complete the survey during this follow-up call,10 they will be sent another email with a link to the survey and if they fail to respond to that email they will receive a second call. All of this is expected to produce a high response rate.
Using this approach, we are able to conduct this survey with a sufficiently large and representative sample, but also in a cost-effective manner. The expected overall response rate will be about 85 percent.
The nature of the online and phone formats of the survey we will implement allow for data quality control measures to be built in to the data collection process. The survey is programmed with skip patterns to both reduce burden on the respondents and the amount of data cleaning that will need to be conducted later. All telephone interviewers will be trained in conducting the interviews and some calls will be monitored for quality assurance. Once the data file is compiled, data quality control checks will be completed using SAS or SPSS programming techniques to check for inconsistencies in the data. Where appropriate, answers given in the “other” category will be up-coded for inclusion in the analysis.
B4. Pretesting of Surveys
We have conducted limited pretesting of the items designed specifically for this survey to ensure clarity, and have administered the full survey to nine respondents whose roles are similar to those we will sample for the full administration to ensure that the respondent burden does not exceed our estimates. This pretest confirmed that our burden estimate of 20 minutes for a respondent to read the instructions and then fill out the survey in full is conservative.
B5. Contact Information
BPA Contact:
Emily Rosenthal (Project director)
Research Analyst
Berkeley Policy Associates
440 Grand Avenue, Suite 500
Oakland, CA 94610
510-465-7884
Hans Bos (Lead methodologist)
CEO
Berkeley Policy Associates
440 Grand Avenue, Suite 500
Oakland, CA 94610
510-465-7884
WestEd Contact:
Kenwyn Derby
Research Associate
WestEd
730 Harrison St.
San Francisco, CA 94107
415-615-3279
References for Part B
Kittleson, M. (1997). Determining effective follow-up of e-mail surveys. American Journal of Health Behavior, 21(3), 193-196.
Mertler, C. A. (2003). Patterns of response and nonresponse from teachers to traditional and web surveys. Practical Assessment, Research & Evaluation, 8(22). Retrieved February 7, 2007 from http://PAREonline.net/getvn.asp?v=8&n=22.
National Center for Education Statistics. (2006). Common Core of Data Public Elementary/Secondary School Universe Survey Data: School Year 2004-2005, U.S. Department of Education. Washington, DC: National Center for Education Statistics.
Punch, K. F. (2003). Survey research: The basics. London, England: Sage Publications.
1 The differences between the versions of the survey are small. Each survey respondent group is asked to report about their particular jurisdiction (e.g., teachers are asked about their school, while others are asked about their district). Teachers are also asked more specific questions about what grade levels and subjects they teach.
2 The elementary level includes teachers who provide instruction classified by state and local practice as elementary and includes any span of grades not above grade 8. The secondary level includes teachers who are classified by state and local practice as secondary and composed of any span of grades beginning with the next grade following the elementary grades and ending with or below grade 12. Ungraded teachers are teachers in a state who instruct classes or programs to which students are assigned without standard grade designation. Middle School or Junior High School teachers may be included in either the elementary or secondary level based on how they are categorized by their state or local education agency, but none are double-counted here.
3 These numbers come from the following data source: National Center for Education Statistics. (2006). Common Core of Data Public Elementary/Secondary School Universe Survey Data: School Year 2004-2005, U.S. Department of Education. Washington, DC: National Center for Education Statistics.
4 See previous note for reference.
5 See previous note number 3 for reference.
6 In the teacher survey, we include a flag to identify whether CTA members being surveyed are active teachers or are in some other professional category.
7 To assess the likelihood of such bias we will explore the possibility of comparing membership demographics to other available data on teacher (or other respondent groups) characteristics and reweight the sample to adjust for any major discrepancies.
8 We are assuming that most of these member organizations have some of this basic information about their members. For example, we assume that the California Teachers Association would be able to provide us with a list of all of their members who are FTE teachers and an indication of what grade level they teach (e.g., elementary or secondary).
9 Unlike stratification, which increases precision, oversampling of specific subgroups would reduce the overall statistical precision of the survey findings. Hence, we will minimize any oversampling we might do.
10 We expect most respondents to complete the survey during the follow-up phone call.
| File Type | application/msword |
| File Modified | 0000-00-00 |
| File Created | 0000-00-00 |
© 2026 OMB.report | Privacy Policy