Att_Supporting_Statement_Part B_MAP

Because this is an efficacy study rather than an effectiveness study, we will be focusing on schools and districts willing to use the intervention and who are willing to participate in this experiment. This includes districts in which the implementation of MAP appears to be a collective decision involving both administrative and instructional staff. Participant schools will be drawn from schools electing to initiate the MAP assessment system in mathematics and reading/language arts and its associated training regimen for the 2008-09 school year. The pool of potential districts includes only those schools that have signed up for the MAP assessment and training. Before signing up, these schools would have been visited by representatives of NWEA describing the assessment and training battery. Conversations with NWEA staff revealed that NWEA has a set of “readiness” criteria for using the MAP system, and will recommend to schools that those schools who do not meet those criteria not sign up for the MAP system. This is a standard part of NWEA’s recruiting and is not a feature of this study. In addition, as has been noted elsewhere, over 99% of schools who use the MAP system do so for more than one year, indicating a high level of satisfaction with the system and “buy-in” by teachers and administrators.

Districts that sign up for MAP training are not automatically enrolled in the study; rather, they are given a detailed description of the study and asked if they would like to participate. At the time of recruitment, districts and schools will be fully informed of the features of the study design. The Memo of Understanding will describe the assignment process in detail and it will provide assurances that the delayed treatment for the control condition will be offered in year 3.

Teachers assigned to the no M+Tr condition will receive the schools’ customary form of professional development. We will encourage principals to assess the extent to which the M+Tr participation duplicates other professional planned development activities. M+Tr participants would be expected to complete non-duplicative professional development activities.

The study will engage 42 elementary schools (see power analysis below for more details) with a total count of about 168 teachers (about 4 per school). The 4th and 5^th grade teachers of reading/language arts and mathematics from all schools will be involved in the study in either the treatment or control group. A more formal discussion of the power analysis is in section 2C below.

The sample to be used is restricted to those schools that have already signed up (that is, have a contract with NWEA) to use the MAP system and its associated training. In that sense, the study is not representative of the nation. However, it is representative of schools that have allocated resources and have planned to use the MAP system and training, and have worked to NWEA to ensure that they have the appropriate level of readiness (which is mostly restricted to having an infrastructure that can handle the rigors of the assessment system), and currently includes up to 10% of the districts in the country. Schools that are not interested in using MAP, or who could not do MAP even if they wanted to because of infrastructure issues, would be inappropriate to include in the sample.

This study uses a cluster randomized design, in which individual schools will be assigned both a treatment and control group at grade level four and five. The overall design for the intervention arm of the proposed RCT is presented in Table 1. The design allows for a randomized test of the MAP program in which teachers and students in grades 3-5 will all eventually receive the MAP intervention over the course of the study (years 1 and 2) or in the following year (year 3). This design also allows for a “typical” roll-out of the program, as schools occasionally phase in MAP and its training across grades over a period of a couple of years.

Table 1

School Type 1 (4^th grade wins the toss)				School Type 2 (5^th grade wins the toss)
Year	Grade			Year	Grade
Year	3	4	5	Year	3	4	5
1		T₁ S₁		1			T₁ S₁
2	“T”	T₂ S₂		2	“T”		T₂ S₂
3			T₁	3		T₁

The designation of T₁ in Year 3 for the control condition is a delayed treatment for the control group, included to enhance the likelihood that schools will agree to randomization and participate in the study. The “T” in Year 2 for third grade is included as an incentive for the schools to retain the control group (either grade four or grade five) for the full two years of the study. Since grade three is not included in the study, this provides schools the opportunity to phase in the MAP program in each grade (3-5), one year at a time, while maintaining a control group for two years.

We assume a high response rate (over 90%) because the measures being used at the student level include state tests, which all students are required to take, and the MAP assessments itself, which, again all students will be required to take. The developer has processes in place to ensure that students who are not present the day of the test are flagged so teachers and administrators\leaders know their test results are needed. The system is computer-based and placed on the in-school server, so testing can be done at any time. The teacher measures include observations, which will not require any special burden on teachers. Other measures including the teacher and administrator\leader surveys will be collected online, which allows for easy tracking to ensure all potential respondents have answered the appropriate questions, and reminders can be sent to those who have not filled out the questionnaires.

Information Collection Procedures

Statistical Methodology for Sample Selection

We will use a cluster-randomized design where the school will be the unit of assignment. In Year 1, one-half of the schools will receive, at random, training (Tr) and access to MAP results (M) in grade four, with grade five conducted in a business as usual (BAU) fashion. The other half of the schools will receive training (Tr) and access to MAP results (M) in grade five, with grade four conducted in BAU fashion. In the second year of the project, grade three classes in all schools will receive MAP training and access to map results as an incentive to continue participation in the study. For clarity of this presentation, we refer the MAP testing and training components as the “M+Tr” condition. The basic research design is presented as Figure 1.

Figure 1

Year 1 Year 2

R_Schools

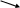
Here, schools will be randomly allocated to the M+Tr in either grade four or grade five in Year 1. Eligible 4^th and 5^th grade teachers, within participating schools and their students will be the study participants. The “Y-bars” in Figure 1 refer to generic pre- and post-test measures obtained for either teachers or students. The “I” or “C” superscript indicates whether the teacher involved was assigned under the intervention or control condition in year 1. The numeric subscript indicates if the measure was obtained in year 1 or year 2. Specific outcomes are described in a subsequent section.

In Year 1, outcomes for teachers and students in the M+Tr condition will be compared to the performance of participants in the BAU condition. The teachers from the M+Tr condition in Year 1 will be followed into the second year of the study with a new cohort students. Because teachers in the intervention condition will have been trained in Year 1, the intervention in Year 2 will be simply access to the MAP testing results (M) for the now new cohort of students.

This revised design addresses three concerns identified in this study’s original design in which 4^th and 5^th grade teachers were randomly assigned to a treatment and control condition within a school.

First, randomly selecting schools to a treatment and control condition prevents contamination across conditions due to interactions among intervention and control teachers. The MAP intervention entails training teachers in the use the MAP testing system and to differentiate their instruction based on the results of testing occasions. All of the training is framed within the use of the MAP system. Because only those teachers in the MAP +T condition will have access to the MAP test results, it is not possible for this aspect of the intervention to be shared across participants in the MAP+T and BAU conditions. On the other hand, it is conceivable that teachers in the intervention condition could share pedagogical strategies with teachers who were not trained in the MAP system. But, since the training for MAP+T participants is so highly connected with the use of MAP testing results, the prospects of contamination by this route are minimal.
Second, because all 4^th or 5^th grade teachers within a given school are included in the study, the possibility that students in treatment schools could get various combinations of exposure to the MAP program over the two year study is eliminated. In the previous teacher level design, some 4^th grade students would have been instructed by a MAP teacher, while others would not. When these students transitioned to 5^th grade, some would receive additional instruction by a new teacher who had been assigned to MAP in Year 1, while other would not. This uncontrolled “assignment” to different doses of MAP would make the analyses of the second year data difficult to interpret.
Finally, individuals knowledgeable about MAP-like professional development programs noted that implementation is unlikely to be accomplished fully in the first year. And, given how long it takes for the training to be “rolled-out”, there would be a limited amount of time (the end of January to mid-March) available for teachers to use MAP-based data to differentiate their instruction before statewide testing would begin. This would likely result in an underestimation of the effects of M+Tr. We do not expect a significant effect on either teacher or student performance during the first year of the study, based on the content of the trainings, as well as the timing of the trainings. As the trainings are currently spaced out, teachers would not receive training on differentiating instruction based on MAP results until late January. Thus, there would only be a short time for teachers to implement their training before students are tested using the state standardized tests. Therefore, we choose not to try and follow students over a two-year period, but rather focus on teachers over the two year period with a new cohort of students each year, students who would not have been exposed to teachers trained in the Year 1 of the study.

Because the pool of schools for this study is limited, by necessity, to those who are interested in using NWEA’s M+Tr system, to enhance willingness to participate in the study, a delay-treatment control design will be used. All districts/schools who sign-up for NWEA’s MAP program will be informed that one grade level at grade four and five will be offered the training and MAP in 2008-2009. In 2009-2010, all participating schools will receive the NWEA program at grade 3. In 2010-2011, the grade level not receiving M+Tr in 2008-2009 (i.e., the control group) will receive the program. The training that is paid for by the study would be the same training available to schools that use the MAP system and will be provided at no cost to the district at grades 3 through 5.

Estimation procedures / Analysis methods

Objective 1: Estimating Effects

In Year 1, outcomes for teachers and students in the M+Tr condition will be compared to the performance of participants in the BAU condition. The teachers from the M+Tr condition in Year 1 will be followed into the second year of the study with a new cohort students. Because teachers in the intervention condition will have been trained in Year 1, the intervention in Year 2 will simply be access to the MAP testing results (M) for the new cohort of students.

The design allows us to test three policy-relevant aspects of the NWEA intervention package.

The first question pertains to the immediate impact or effects of the intervention. The design provides two bases for estimating these effects. By comparing the average student achievement gain (or level) between participants in the MAP v. noMAP conditions in Year 1 we will be able to answer the question “Does the MAP intervention (i.e., training plus formative testing feedback) affect the reading and mathematics achievement of students?” We will also be able to examine differential effects by comparing across conditions in Year 1 within strata defined by categories of initial achievement. In terms of the notation introduced in Figure 1 we will be testing the null hypothesis that ( ) – ( )=0. We will refer to MAP effects estimated in this fashion as MAP* effects.

The second policy-relevant question concerns the sustainability of the NWEA/MAP program effects on teacher performance. In as much as the initial group of M+Tr teachers can be followed through the end of the second year of the project, we will be able to answer the question “Do the effects on teacher performance (if any) of M+Tr persist over time when delivered under the M (only) condition to a new cohort of students?” In terms of the notation introduced in Figure 1 we will be testing the null hypothesis that ( )-( )=0.

The third policy-relevant question that can be addressed using this design concerns how long it takes to see M+Tr effects. The delayed-treatment control condition provides an alternative way of determining immediate impacts of the MAP intervention. By pre-testing students, we can assess gain (or residual gain) in performance at the individual student level. Here, the relative gain (or level) in student performance due to MAP can be assessed within each treatment condition teacher by comparing achievement gain (level) for students in the year 1 M+Tr cohort with the gain (level) for students in the year 2 M only cohort. We refer to MAP effects estimated in this fashion as MAP** effects.

Objective 2: Implementation Assessment

The implementation study will focus on the extent to which there is school-to-school and teacher-to-teacher variability in the extent to which elements of the MAP training is learned and utilized in the school and classroom. This aspect of the proposed study will address three questions: (1) “What effect does MAP data and training have upon instructional practices?” (2) “Do teachers continue to use MAP results to alter their instructional practices in the subsequent year when only on-line resources are available (no further MAP training)?” and (3) “To what extent does variation in the implementation of MAP or variation in receipt of training account for the effects (or lack of effects) on teacher instruction and student achievement outcomes?

The MAP testing program and training (M+Tr) involves multiple intervention components. As shown in Figure 1, successful completion of the 4-step (session) training sequence by teachers is central to the success of NWEA’s intervention package in enhancing learning outcomes for students. In addition to the knowledge and skills highlighted in the training component, participants need to learn how to apply (transfer) this new knowledge and associated pedagogical skills in their classrooms so as to best meet the needs of their students (as indicated by the formative assessment). Training for the leadership team (e.g., principals) is also provided as part of the MAP training, and it appears to be an important contextual component of the overall intervention.

Given the presence of multiple, interdependent program components that are delivered over an extended time frame, there are numerous possibilities for there to be slippage between the program-as-conceptualized and the program-as-implemented. As such, in addition to addressing question of the effects of the NWEA’s M+Tr intervention, we will address the fidelity with which the M+Tr and M-only programs are implemented.

In addition to assessing the efficacy of NWEA’s MAP testing and training program, this study can serve as a model for assessing other similar assessment tools that are emerging in this field. Similar products are available from ETS, Scantron, PLATO Learning, ThinkLearning, and a host of others entering the market.

To test these hypotheses as they apply to student level outcomes, we will use Raudenbush and Bryk’s (2002) statistical models for analyzing data that are hierarchically structured. Actual statistical modeling will utilize the HLM statistical package (Raudenbush et al. 2004). Hierarchical modeling is not necessary to analyze teacher level outcomes as schools are regarded as fixed effects.

In the subsections below we provide the full specification for the hierarchical models that will be used to test the hypotheses mentioned above as they apply to student level outcomes. The model used will depend on the hypothesis being tested. There are two types of hypotheses that will be tested, those that involve comparisons across treatment conditions and those that involve comparisons across years within teachers. We consider first models for testing hypotheses involving comparisons across treatment conditions.

Hierarchical models for testing comparisons across treatment conditions

The two hypotheses that will be tested using the model described below are MAP*, which compares student improvement in year 1 across treatment conditions. First we present the analysis for student outcomes and then for teacher outcomes. The statistical model that addresses the first research question for student outcomes is descried via a two-level model (see below) where students are nested within schools. This analysis is conducted for each grade separately.

Level 1: Students-Within-Schools. Our system of equations begins at the student level. Equation 1 describes the relationship between student achievement, individual background characteristics, and random variation among the students in each school.

(1)

In this model,

= achievement of student i, in classj j; and

= vector of student characteristics (e.g., race/ethnicity, free and reduced-price lunch status,prior academic achievement) for student i, in school j (centered around their grand means across the sample).

= vector of teacher characteristics ((e.g., teaching experience, degrees held, gender, grade, average math and reading scores for prior classes, and prior professional development) or teacher fixed effects dummies (three dummies included in the model) for teachers within school j (centered around their grand means across the sample).

Therefore,

= average achievement in school j, adjusted for student and teacher effects;

= the vector of relationships between individual student characteristics and student achievement in school j ;

= the vector of relationships between individual teacher characteristics (or teacher fixed effects dummies) and student achievement in school j;

= the error associated with each student (adjusted for student and teacher effects); and

= the residual variance between students within schools.

Level 2: Schools. Given that random assignment occurs at the school level, program impacts are estimated at the school level of the system of equations:

(2)

where,

=1 if school j is in the treatment group, 0 otherwise;

= vector of characteristics of school j.

Therefore,

= the average treatment effect.

= vector of coefficients measuring associations between school level covariates (e.g., school characteristics) and average school achievement.

= vector of coefficients measuring average association between student covariates and response;

= vector of coefficients measuring average association between teacher covariates and response;

and

= the residual variance between schools.

If necessary, this two-level system of equations will be estimated separately within each district and translated into an effect-size metric (i.e., the impact estimate divided by the standard deviation). The average effect will then be estimated by taking a simple average of the impact estimates across all the districts in question. Though we can explore variation across districts, we are likely to lack the statistical precision to discern whether or not the observed variation represents systematic differences in program effects.

Hierarchical models for testing comparisons within teachers across years

The statistical model that addresses the second research question for student outcomes is descried via a two-level model (see below) where students are nested within schools. This analysis is also conducted for each grade separately.

Level 1: Students-Within-Schools.

(3)

In this model,

= achievement of student i, in school j;

Year_ij = Variable which is 1 if measurement is taken in second year of study, 0 otherwise; and

= vector of student characteristics (e.g., race/ethnicity, free and reduced-price lunch status, prior academic achievement) for student i, in school j (centered around their grand means across the sample).

Therefore,

= average achievement in school j, adjusted for student and teacher effects;

= the vector of relationships between individual student characteristics and student achievement in school j ;

= the vector of relationships between individual teacher characteristics (or teacher fixed effects dummies) and student achievement in school j ; and

= the average impact of year on student achievement for school j;

= the error associated with each student (adjusted for student and teacher effects); and

= the residual variance between students within schools.

Level 2: Schools:

(4)

where,

= vector of characteristics of school j.

Therefore,

= vector of coefficients measuring associations between school level covariates (e.g., school characteristics) and average school achievement.

= vector of coefficients measuring average association between student covariates and response;

= vector of coefficients measuring average association between teacher covariates and response;

= average year effect

and

= the residual variance between schools.

Similarly, two-level models (where teachers are nested within schools), like the ones described above, can be employed to determine the treatment effects on teacher outcomes.

Estimates of Effects on Teaching Practice

The key research questions here concern whether access to frequent formative assessment data and training in differentiation of instruction for teachers, as a package, improves instructional practices of teachers. Multi-level modeling is not needed for teacher level analyses. Thus, for comparisons across treatment conditions a standard regression model will be used. For comparisons within teachers a variation of a one-sample t-test will be used where teacher scores are adjusted to account for fixed school and grade effects prior to conducting the t-test.

The primary analysis of the effects of MAP on teacher practices will use indices derived from the classroom observations. The secondary analysis will rely on multiple indicators of teacher practice based on responses to surveys, plus the data from logs and from classroom observations. As indicated earlier, the validation study component for Year 1 is designed to determine how to accurately and cost-efficiently assess implementation fidelity at the teacher and student level. The emphasis of this study is on the interrelations (if any) among alternative methods for assessing implementation fidelity and relative strength of the M+Tr v. BAU contrast.

Analysis on the Effects of Intervention When Implemented With Varying Degrees of Fidelity

The final policy question pertains to the effects of the NWEA intervention when it is implemented with varying degrees of fidelity across teachers, school and students (see objective 2: Implementation Assessment, Item 2B, p. 7 above)^¹. The results of this analysis will provide important information about how fidelity of implementation (in both conditions) affects the outcomes of the study. Because there is no obvious statistical solution to account for the partial receipt or delivery of the intervention (or contamination of the control condition due to partial cross-overs), the results based on any analysis for this question will not be unbiased. The idea is that the fidelity measures may be related to unobserved student, teacher, and school variables and, therefore, the estimates may be biased, and should not be interpreted as casual effects.

However, using the indices of intervention fidelity (to be developed), it will be possible to examine the likely influence of incomplete MAP receipt (training and or testing) on teacher classroom practices, and in turn, on student achievement. These analyses will treat achieved fidelity as a moderator factor.

The two-level HLM model described in detail in the introduction of this section will be augmented by the inclusion of implementation fidelity indices at both levels of the model (the two-level model is described below). The models we will use to assess the effects of variation in implementation are simply expansions of the model described earlier. But unlike the covariate included in the full description of the two-level model (that is the level-1 pretest achievement score), the covariates to be included in this analysis are not independent of treatment assignment. We regard the results from this aspect of the study as non-experimental.

An analysis of the effects of variability in the implementation fidelity on student achievement will be undertaken using the best combination of fidelity measures and standardized achievement tests for n=8 students per class. Sampling is being used in the fidelity study to minimize data collection burden for teachers. An objective of the Year 1 phase of the study is to examine the psychometric quality of several approaches (surveys, logs, observations) to assessing fidelity, and to examine the extent to which data from these methods converge. The sample size (n=8) will be sufficient to detect validity coefficients of 0.40 or greater. Assuming a boost in the variance accounted for at level 2, the sample size will be sufficient to assess the linkage between fidelity level and student outcomes.

There is no guidance in the literature on how to measure the fidelity with which the key component of the MAP program -- differentiated instruction – is implemented in classroom settings. As such, this project is developing and pilot testing three approaches for literacy/reading. The sampling will be done within groups of students identified as in the lower or upper quartile on state reading tests. This assumes that we will be able to locate and select classes with mixed ability levels. Data from NWEA indicates that this is possible. Within the high and low reading readiness subgroups students will be randomly selected. Student with special needs (e.g., gifted or students with IEPs) will not be included in these ability subgroup pools.

The full model to account for differences in implementation fidelity could include the following covariates:

Level-1: Students.

Attendance,
Teacher ratings of engagement, and
Teacher ratings of student competence.

Level-2: Teachers/Classes. Indices of differentiated instruction:

From the CIERA, indices of the diversity in grouping, instructional activities, foci, materials, style, expected response;
From Logs, indices of diversity in content coverage, difficulty of instruct; and
From Surveys, self-reported indices of professional development, instructional strategies, knowledge of data use, knowledge of differentiated instructional strategies, topical coverage.

The following school. indicators are also included at the second level:

Attendance of school leaders at MAP training,
Administrative support for MAP-like programs, and
Nature and level of instructional improvement efforts at the school.

Specifically, the first part of the fidelity analysis will model student outcomes such as student achievement. The fidelity analysis on student outcomes can also be modeled via a two-level HLM, where students are nested within teachers. Specifically, for student i within teacher j the level-1 model is

the second level model for the intercept is

and the second level model for the m level-1 coefficients is

where X is a row vector that includes student measures of fidelity such as attendance, engagement, and competence (see page 19), and other covariates such as student gender, race, SES, and previous achievement, is the average value of the outcome across all students, teachers, and schools, the ’s are the effects of the student fidelity measures that need to be estimated (and m is the number of level-1 predictors), Z is a row vector that includes teacher measures of fidelity such as professional development (including teachers attending MAP training sessions and using online resources in the M+Tr condition and equivalent activities for the control teachers), and measures from classroom observations, teacher surveys and teacher logs (see pages 16-19), is column vector of the effects of the teacher fidelity measures that needs to be estimated, T is a row vector of teacher characteristics such as teacher experience, education, etc., is column vector of the effects of teacher characteristics that needs to be estimated, S₁ is a row vector that includes school measures of fidelity such school leaders attending MAP training sessions, administrative support of MAP-like programs, and instructional improvement efforts in the school (see pages 14-15), is column vector of the effects of the school fidelity measures that needs to be estimated, S₂ is a row vector of school characteristics such as school composition, etc, is column vector of the effects of the school characteristics that needs to be estimated, is a student-specific residual, and is a teacher-specific residual. The main objective in this analysis is to compute all the ’s (in particular those in ). Grade could also be included as a binary indicator at level 1.

The second part of the fidelity analysis will model teacher outcomes. The fidelity analysis on teacher outcomes can be modeled via a teacher-level regression. Specifically, for teacher j the regression model is

where X is now a row vector of classrooms averages of student fidelity measures, is now a column vector of the classroom average student fidelity effects that need to be estimated, and all other terms are as defined above. The objective of this analysis is to compute the ’s and ’s. Grade can also be included as a binary variable.

In both types of analyses the fidelity measures will be modeled as linear and non-linear (e.g., polynomial or dummies) effects in both types of analyses. The idea is to determine which coding produces a better fit.

Degree of accuracy needed

The proposed study entails two experimental-based hypotheses for which statistical power can be assessed. These include:

Does the MAP intervention (i.e. training plus formative testing feedback) affect the reading and mathematics achievement of 4^th and 5^th grade students^²?
What effect does MAP data and training have upon math and reading instruction?

To assure that statistical power is sufficient to adequately address either hypothesis, statistical power is estimated for each, separately. The needed sample size will be based on the hypothesis that requires the largest number of schools. These power analyses assume that schools will be treated as fixed effects. As such we assume that it is unnecessary to generalize the results of this study beyond the actual schools represented in this sample. Since schools are treated as fixed effects, such a generalization would be unwarranted.

The power computations were conducted using the ANCOVA framework and assuming two-level balanced cluster randomized designs (see Hedges & Hedberg, 2007). The power of the two-tailed t-test at level α is:

p₂ = 1 – Η [c(α/2, 2m-q-2), (2m-q-2), λ_A] + Η [-c(α/2, 2m-q-2), (2m-q-2), λ_A],

where c(α, ν) is the level α one-tailed critical value of the t-distribution with ν degrees of freedom [e.g., c(0.05,20) = 1.72], and Η(x, ν, λ) is the cumulative distribution function of the non-central t-distribution with ν degrees of freedom and non-centrality parameter λ_A.

Also, m is the number of clusters (schools) in each condition (2 conditions overall), q is the number of level-2 covariates (1 in this case), and λ_Ais the non-centrality parameter of the test statistic that has the non-central t-distribution when the null hypothesis is false. When covariates are included in the model, the non-centrality parameter is defined as

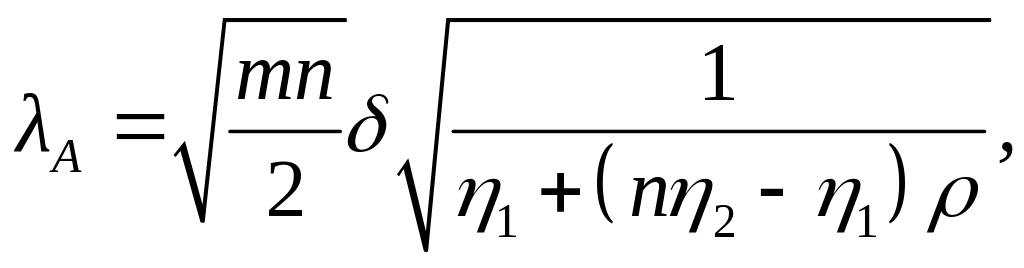
where n is the number of level 1 units (e.g., students or teachers) within level 2 units (e.g., schools), is the treatment effect, is the nesting effect, and the η’s indicate the proportion of the variances at each level of the hierarchy that is still unexplained (percentage of residual variation). For example when = 0.25, this indicates that the variance at the student level decreased by 75 percent due to the inclusion of covariates such as pre-treatment measures at the first level.

Sample Sizes

The power analysis for student and teacher outcomes assumes a two-level design, in which schools are randomly assigned to a treatment and a control. The first level units are students/teachers and the second level units are schools.

Student Outcomes

A meta-analytic study of the effects of formative assessment on learning outcomes (Nyquist, 2003) reveals that the effects of feedback on achievement depend on the quality of the assessment/feedback process that is delivered. It can range from about 0.15 to 0.50, with the highest effects appearing when feedback provides directions for improvement, explains why an answer is incorrect, provides a goal and so forth. The studies reviewed in that meta-analysis were mainly conducted in laboratory settings or in classrooms where the researcher had greater control over the delivery of the feedback and other important elements of formative assessment (e.g., use of meta-cognitive strategies to improve performance, goal specification). Because we expect that teachers will vary in the fidelity with which they use formative assessment in their class, we have chosen a fairly conservative effect between the extremes reported in Nyquist’s thesis (0.25).

To estimate the sample size for this study we assume that pretest (previous standardized tests) scores on the outcome measure explain 75% of the variation in the outcome at the first level and none of the between grade variance. We also assume that a grade level covariate (e.g., school or teacher level variable) is introduced at level 2 and explains 50% of the variance at the second level and none of the variance at the first level. We also assume intraclass correlations of .15 and 0.10, 20 students per classroom, 4 teachers per school and an effect size estimate of 0.25.

Given the assumptions listed above, the power calculations for this two-level design indicate that to achieve a power of .80 about 42 schools are needed when the intraclass correlation is 0.15, and about 30 schools when the intraclass correlation is 0.10.

Teacher Outcomes

To estimate the sample size for teacher outcomes we assume that a teacher level variable introduced at the first level will explain 50% of the variation in the outcome at the first level and none of the between grade variance. We also assume that a grade level covariate (e.g., school level variable) is introduced at level 2 and explains 50% of the variance at the second level and none of the variance at the first level. We also assume intraclass correlations of .15 and 0.10, 20 students per classroom, 4 teachers per school and an effect size estimate of 0.48. An analysis of CIERA-based classroom observations (Taylor et al, ) within 25 Reading First and 16 non-Reading First schools in Wisconsin showed that teachers in Reading First schools were more likely to engage in instruction involving small groups of students than teachers in non-Reading First schools (Hudgens/LPA, no date). Our calculations, based on the differences in aggregate proportion of small group instruction across conditions, revealed an effect size of 0.48.

Given the assumptions listed above, the power calculations for this two-level design indicate that to achieve a power of .80 about 28 schools are needed when the intraclass correlation is 0.15, and about 26 schools when the intraclass correlation is 0.10.

Methods to maximize response rates

As was stated earlier, the sample population consists only of those schools that were planning on using the MAP and its associated training. Thus, the schools, including teachers and administrators/leaders, will have already been prepared to go through the intervention, as opposed to other designs where the schools may or may not have been interested in the intervention before being approached by the study team. NWEA reports that more than 95% of the schools that participate in the training continue for 2 or more years (almost 100% after 1 year). Given this fact, and the 20-plus years of experience NWEA has had with this program, we feel confident in assuming that the schools in which this program is implemented are excited about the program, and want to do it, providing the institutional support that is crucial to full participation. In addition, REL Midwest will cover the cost of the training, freeing up dollars the school might have already committed to the program to help defray possible expenses that might be study related, such as union contracts which would require payments to teachers for their time beyond the training.

However, we recognize the study will add some additional burdens to teachers and administrators/leaders in terms of data collection. In some cases, the data to be collected do not require any additional effort from respondents. For example, the student achievement data will be gathered from existing records. Other data, such as the teacher survey and teacher logs, will require follow-up to maximize the response rates. We are very sensitive to minimizing the amount of time respondents will spend on the data collection, which helps to increase response rates. In addition, electronic data collection (e.g. online survey tools) will be used to allow for “anytime” entry of data. We will send reminder e-mails to study participants with embedded links to the appropriate site where they can enter their responses.

In general, there are two main principles we will use to increase response rates:

Justification: Providing respondents with sufficient information about why their participation is important. District and building administrators\leaders will be given information about the context of the study, the importance of their participation, and advance notice of site visits. Additionally, school and district leadership will have committed to participation in this data collection effort when they sign a Role and Responsibilities document that indicates their agreement to participate in the study and specifies what types of involvement is needed from them.
Accommodation: Working with the respondents’ schedules. Field researchers will be flexible in scheduling interviews with administrators\leaders and will make efforts to complete interviews at the respondent’s convenience on site. However, if this is not possible, interviewers will seek to complete the interviews over the phone.

The ability to communicate the importance of the respondents’ participation in the study and the ability of the study team to be flexible in seeking these interview data are expected to result in high response rates.

School- and teacher-level attrition. As stated, we anticipate little school-level attrition from our samples given NWEA’s reported past experience with their clients. Retention within this intervention is typically 100% during the first year. Additionally, all schools-level participants (districts and schools) have volunteered to be a part of the study. Treatment teachers will be involved in the intervention the first year and control teachers will receive the full treatment in Year 2 of the study.

Student-level attrition. In order to assess the latent structure of missingness (attrition, maturation, and other qualities), data could be reorganized by occasions of measurement (Raudenbush & Bryk, 2002)and a Level-1 HLM used to generate the required regression coefficients and standard error estimates for the subsequent analyses. For students with missing data, these estimates would be substituted in Model 2. This model adjusts the estimates for students by accounting observed and missing data patterns for each student rather than using multiple imputation methods which can be rather cumbersome and assume that data are missing at random^³.

Tests of procedures to be undertaken

All of the measures used in this data collection, except the measure examining teacher knowledge of concepts taught during the training (which is not considered as part of the burden estimate), are copyrighted measures that have been used in previous studies. Measures from the Study of Instructional Improvement (SII, 2001), including the Teacher and School Leader Questionnaire, and the Student Rating Form, will be used in this study. In addition, Instructional Logs, which were also developed for use in the SII (Rowan et al., 2004), will be used. Camburn & Barnes (2003) present evidence on the validity of these logs in represented enacted curricula. For the classroom observations we will use an adaptation of the Center for the Improvement of Early Reading Achievement (CIERA) observation system (Taylor, Pearson, Petersen, & Rodriguez, 2003).

Individuals consulted on statistical aspects of design

David Cordray, Professor of Public Policy, Professor of Psychology Quantitative Methods and Program Evaluation, Department of Psychology and Human Development, Vanderbilt University

Larry Hedges, Board of Trustees Professor of Statistics and Social Policy, Northwestern University

Spyros Konstantopoulos, Assistant Professor, School of Education and Social Policy, Northwestern University

References

Camburn, E. & Barnes, C.A. (2003). Assessing the validity of a language arts instruction log through triangulation. Unpublished report. University of Michigan.

Hudgens, S. (2007). Classroom Observations. Unpublished report. Naperville, IL: Learning Point Associates.

Nyquist, J. (2003). Reconceptualizing Feedback as Formative Assessment: A Meta-analysis. Unpublished Masters Thesis. Vanderbilt University.

Raudenbush, S. W., & Bryk, A. S. (2002). Hierarchical linear models: Applications and data analysis methods (2nd ed.). Newbury Park, CA: Sage.

Rowan, B., Camburn, E., & Correnti, R. (2004). Using teacher logs to measure the enacted curriculum: A study of literacy teaching in 3^rd grade classrooms. Unpublished paper. University of Michigan.

Taylor, B. M., Pearson, P. D., Petersen, D. S., & Rodriguez, M. C. (2003). Reading growth in high poverty classrooms: The influence of teacher practices that encourage cognitive engagement in literacy learning. Elementary School Journal, 104(1), 3–28.

1 When units are randomly invited to participate (or not) in the intervention and fail to enroll, random assignment can be used as an instrumental variable to obtain an unbiased estimate of the impact of the treatment on those electing treatment (see Angrist, Imbens, & Rubin, 1996). It is highly unlikely that in this experiment that the “no shows” will be as crisply defined as required by the Angrist et al. procedure.

2 For student achievement, we will use the state-level standardized test scores for math and reading/language arts. The specific tests will depend upon which state is chosen for study participation. The candidates are Illinois, Ohio and Minnesota. The standard tests used in these states are presumed to be psychometrically adequate.

3 For students that enter during the school-year, MAP testing will be administered to assess the student’s progress to date. All reasonable efforts will be made to gather prior test data on students entering mid-year.

File Type	application/msword
Author	mdawson
Last Modified By	Sheila.Carey
File Modified	2008-01-29
File Created	2008-01-29