Att_NEIREL SS Part B
Att_NEIREL SS Part B.doc
An Evaluation of the Thinking Reader Software Intervention
OMB: 1850-0837
An Evaluation of the Thinking Reader Software Intervention
OMB Clearance Request
Supporting
Statement
Part B
April 2007
Prepared For:
Institute of Education Sciences
United States Department of Education
Contract No. ED‑06‑CO‑0025
Prepared By:
Regional Educational Laboratory—Northeast and the Islands
55 Chapel Street
Newton, MA 02458-1060
Supporting Statement Part B
request for clearance of information collection forms for
an evaluation of the thinking reader software intervention
Study Overview
The Thinking Reader (TR) study will examine the effect of using this software program on 6th graders’ reading comprehension, vocabulary, use of comprehension strategies, and motivation to read. The study design involves within-school random assignment of teachers (and their intact classrooms) into the intervention or control condition. To balance the research activities done within the Northeast region, the Thinking Reader study will take place in the state of Connecticut. During the 2007-2008 school year, districts in Connecticut will have the opportunity to participate in this study, implementing the program with 6th graders. REL-NEI prefers to implement the program in high need, low resource, urban areas (e.g., Bridgeport, Harford, New Haven). Ultimately, 25 schools will participate in the study. We plan to recruit two 6th grade English/Language Arts (ELA) teachers in each of these 25 schools.
Because Thinking Reader is intended to be implemented as part of students’ ELA instruction, the classroom is the most obvious choice as the unit of assignment. However, our team has decided to use the teacher – and his/her multiple classrooms – as the unit of assignment. We found in a prior study that randomizing classrooms within teacher changed the dynamic of the instruction, where the teacher felt like he/she was in competition with the software. Therefore, 6th grade ELA teachers within each school will be randomly assigned into the Thinking Reader or control group condition. We assume that on average, there will be:
Two 6th grade ELA teachers in each school (one treatment and one control teacher in each school)
Each teacher teaches two classrooms (four classrooms in each school, the two classrooms taught by the treatment teacher, and two classrooms taught by the control teacher)
24 students in each classroom
B1. Sampling Variables and Approach
This study involves random assignment of teachers into study conditions, but not random selection of teachers into the sample. This study involves a purposive, volunteer sample of districts, schools, and teachers (and their intact classrooms). This evaluation focuses on high internal validity, and we acknowledge that without random sampling, external validity is limited. Because this research project is driven by regional priorities, the need to distribute research activities across the REL-NEI states, the cost concerns of conducting experimental field trials across many sites, and the intentional focus on high need schools, a probability sample is not feasible. The only part of this study that will involve simple random sampling is the selection of 12 Thinking Reader and 12 control groupwhich one of each teacher’s multiple classroom sections will be chosen for the classroom observations.
The Thinking Reader evaluation will involve approximately 50 teachers of 100 classrooms in 25 high-need1 schools (assuming an average of four classrooms per school). The intervention will focus on students in 6th grade; we assume 24 students per classroom (i.e., 48 per teacher), for a total of 2400 students. To balance the research activities done within the Northeast region, the Thinking Reader study will take place in the state of Connecticut.
We are targeting high-need school districts in Connecticut. Districts in this group are Ansonia, Bridgeport, Danbury, Derby, East Hartford, Hartford, Meridien, New Britain, New Haven, New London, Norwalk, Norwich, Stamford, Waterbury, West Haven, and Windham. We are also prepared to recruit in Vermont and Maine, if needed.We are targeting large, urban, high-need school districts in Connecticut. Connecticut groups its districts into Education Reference Groups (ERGs) for reporting purposes,2 and districts that fit the large, urban, high-need label fall into ERG I. Districts in this group are Bridgeport, Hartford, New Britain, New Haven, New London, Waterbury, and Windham. We will focus on Bridgeport, Hartford, and New Haven, but will also reach out to the other districts in the ERG to achieve our target of 25 schools. Of the seven high-need districts, these three have 76 of the 86 schools in the ERG that enroll a 6th grade and that hold regular school status,3 according to the most recent Common Core Data (2004-2005). Table 1 summarizes the characteristics of these seven 16 districts in Connecticut, based on the 2004-2005 CCD.
Table
1.
Characteristics of Districts to be Recruited
District |
Total Schools |
Total Students |
Percent Classroom Teachers (FTE)Economically Disadvantaged Students |
Percent ELL Students |
Percent Students with IEPs (special education) |
Ansonia |
4 |
2,705 |
46.3 |
3.1 |
10.8 |
Bridgeport |
3534 |
22,264 |
1,249.997.3 |
2,83012.7 |
2,1459.6 |
Danbury |
17 |
9,556 |
27.6 |
15.4 |
11.1 |
Derby |
3 |
1,492 |
37.4 |
7.6 |
10.0 |
East Hartford |
14 |
7,916 |
49.5 |
4.8 |
13.0 |
Hartford |
4136 |
22,296 |
1,458.966.6 |
3,79717.0 |
3,71116.6 |
Meridien |
12 |
8,946 |
54.1 |
7.5 |
13.3 |
New Britain |
15 |
10,936 |
51.3604.2 |
1,59514.6 |
16.41,790 |
New Haven |
4948 |
20,499 |
1,351.371.8 |
2,14210.4 |
1,7278.4 |
New London |
97 |
3,076 |
214.464.1 |
70022.8 |
46415.1 |
Norwalk |
19 |
11,039 |
23.1 |
11.6 |
11.2 |
Norwich |
14 |
4,045 |
52.1 |
8.2 |
14.3 |
Stamford |
20 |
15,077 |
42.7 |
15.0 |
10.9 |
Waterbury |
3027 |
17,896 |
1,213.264.9 |
1,96911.0 |
2,72515.2 |
West Haven |
11 |
7,037 |
44.4 |
5.7 |
6.5 |
Windham |
98 |
3,635 |
262.556.8 |
51314.1 |
56115.4 |
Because Thinking Reader is intended to be implemented as part of students ELA instruction, the classroom is the most obvious choice as the unit of assignment. However, our team has decided to use the teacher – and his/her multiple classrooms – as the unit of assignment. As noted previously, we found in a prior study that randomizing classrooms within teacher changed the dynamic of the instruction, where the teacher felt like he/she was in competition with the software. Therefore, 6th grade ELA teachers within each school will be randomly assigned into the Thinking Reader or control group condition. We assume that on average, there will be:
Two 6th grade ELA teachers in each school (one treatment and one control teacher in each school)
Each teacher teaches two classrooms (four classrooms in each school, the two classrooms taught by the treatment teacher, and two classrooms taught by the control teacher)
24 students in each classroom (48 per teacher, or 2400 total)
We will exclude schools that have only one 6th grade ELA teacher. If a school has more than two 6th grade ELA teachers, we will include and randomize all teachers who wish to participate in the study. We assume a 20% attrition rate at the student level, with 2400 students providing pretest data and 1920 students providing posttest data.
Thinking Reader is server-based software. According to Tom Snyder Productions, the recommended technical specifications for robust performance are:
Server: Must run TomSnyderServer software on Windows 2000/2003, Mac OS X 10.3/10.4, or Netware 6/6.5; Processor: 1Ghz or better; RAM: 1GB or more; Disk Space: 200 MB
Workstations: Windows XP or Mac OS 10.3.4 or later; Processor: 800Mhz or better ; RAM 128Mb or more; Disk Space: 250Mb per title
Network: 100 Mbit wired network or 802.11a/g/n wireless network
Assuming that: (a) at least one teacher (i.e., two classrooms) in each school will be using Thinking Reader, (b) the 24 students in each of her classrooms will need to be on the program three times per week, and (c) the two classes don’t meet at the same time (which is a given in the smaller schools with just one treatment teacher), a minimum of 12 computers per school would be necessary, and 24 computers per school would be ideal. As we proceed with our recruitment and discuss the study with districts and schools, we will be able to determine which schools have the technological capacity to implement the software.
Data analysis
Sample characteristics and baseline group equivalence
We will conduct a series of preliminary data analyses to carefully examine the distribution of teacher (e.g., experience, level of education) and student characteristics (e.g., gender, achievement level on pretest measures) after the random allocation into study groups has been done. In the case of “unhappy” randomization, we will include the variables on which we found statistically significant differences in our analyses to help adjust for baseline differences.
HLM analyses to assess impact on student achievement
This study is intended to assess the effect of Thinking Reader on student reading achievement and motivation. The study is designed as a multi-site cluster randomized controlled trial where 6th grade teachers are randomly assigned to either the Thinking Reader or control group within each participating school. The main research questions are whether students in the Thinking Reader classrooms demonstrate better reading achievement and reading motivation outcomes than students in the comparison classrooms. Given the nested data structure (i.e., students nested within teachers), we will use hierarchical linear modeling (HLM; Raudenbush & Bryk, 2002) to address our research questions.
The analytical model developed for this study attempts to identify the amount of the variance between the treatment and control group and to test its statistical significance. However, it is possible that teachers in different schools have different core curricula, which could explain why the intervention is effective for some students, but not for others. Therefore, an alternative way of assessing the effectiveness of the intervention is to estimate, in addition to the main effect of the intervention, how the treatment effect varies by strata, where each stratum includes teachers who use the same core curriculum before the study started.
Level-1 (student level)
![]()
where
Yi j: outcome measure for student i for teacher j;
Pretesti j: pretest reading score of student i for teacher j, grand-mean centered;
ELLi j: indicator variable representing whether student i for teacher j is an English Language learner;
SpecialEdi j: indicator variable representing whether student i for teacher j is in special education;
Low_Achij indicator variable representing whether student i for teacher j is a low achieving student;
π0j is the average outcome of students for teacher j;
π 1j - π 4j are effect of corresponding variable of student i for teacher j on the outcome measure; and
eij is a random error associated with student i for teacher j.
Level-2 (teacher level)
The level-2 or teacher-level model is composite of multiple equations, one for each coefficient in the level-1 model. We assume the teacher-level average outcome estimated in the level-1 model (intercept π0j) varies randomly across teachers as a function of the teacher-level intervention (the Thinking Reader), the core curriculum used, as well as teacher characteristics such as level of education, certification status, and years of professional experience, within-classroom percentage of ELL students, and percentage of special education students. Other level-1 coefficients (π1j - π 3j) are modeled as having fixed effects at level-2. The level-2 equations are shown below.

where
00 is the average student outcome measure across all teachers (i.e., grand mean);
(Treatment)j is an indicator variable for teacher j received intervention: 1/2=Thinking Reader teachers, and -1/2= control teachers;
01 is the difference between the Thinking Reader teacher’s students and the comparison teacher’s students on average student outcome;
(Stratum1)j, (Stratum2) j, …, and (Stratumk) j are k indicator variables representing a total of (k+1) curriculum strata, each coded as: ½=Stratum k, -½ = otherwise;
02, 03, …, and 0(k+1) are the differences in average student outcome between each of the k strata (curricula) and the omitted reference strata (i.e., fixed strata effects);
(Treatment)j*(Stratum1) j, (Treatment)j*(Stratum2) j, …, and (Treatment)j*(Stratumk)j are k intervention-by-school interaction terms;
0(k+2), 0(k+3), …, and 0(2k+1) are the coefficients for the k interaction terms;
(Education)j is an indicator variable for the teacher who taught classroom j received Master degree: 1=MA, and 0= BA;
0(2k+2) is the effect of teacher education level on the outcome measure;
(Certificate)j is a certification indicator variable for teacher j: 1=Yes, and 0= No;
0(2k+3) is the effect of teacher certification on the student outcome measure;
(Experience)j is the measure of experience teaching for teacher j;
0(2k+4) is the effect of teacher’s teaching experience on the student outcome measure;
(%ELL)j is the proportion of ELL students in the classrooms of teacher j;
0(2k+5) is the effect of proportion of ELL students on the student outcome measure;
(%SpecialED)j is the proportion of special education students in the classrooms of teacher j;
0(2k+6) is the effect of proportion of special education students on the student outcome measure; and
v0j is a random term associated with unmeasured effects on the student outcome measure of teacher j.
All the coefficients in the level-2 model are adjusted for student pretest scores, ELL, and special education status. Of primary interest among the level-2 coefficients is 01, which represents the intervention’s main effect on the outcome. A statistically significant positive value of 01confirms the hypothesis that students of a teacher implementing Thinking Reader demonstrate better outcomes than their counterparts in the control teachers’ classrooms. The interpretation of the intervention’s effect, however, might need to be qualified if significant treatment-by-strata interaction effects are found, as significant interaction effects indicate that the intervention’s effect differs significantly for different core curriculum rather than having a common effect across all core curricula.
Subgroup analyses
We are particularly interested in comparing three subgroups of students with their counterparts: low achievers, special education students, and English language learners. We test these secondary research questions by including cross-level interaction terms in the analytical model used to study the primary research question. . In essence, we are interested in examining whether the Thinking Reader intervention affects the slope associated with the subgroups. We use the ‘Low Achiever’ subgroup to illustrate the analytical approach.
Level-1 (student level)
![]()
where
Yi j: outcome measure for student i for teacher j;
Pretesti j: pretest reading score of student i for teacher j, grand-mean centered;
ELLi j: indicator variable representing whether student i for teacher j is an English Language learner;
SpecialEdi j: indicator variable representing whether student i for teacher j is in special education;
Low_Achij indicator variable representing whether student i for teacher j is a low achieving student;
π0j is the average outcome of students for teacher j;
π 1j - π 4j are effect of corresponding variable of student i for teacher j on the outcome measure; and
eij is a random error associated with student i for teacher j.
Level-2 (teacher level)
The level-2 or teacher-level model is composite of multiple equations, one for each coefficient in the level-1 model. We assume the teacher-level average outcome estimated in the level-1 model (intercept π0j) varies randomly across teachers as a function of the teacher-level intervention (the Thinking Reader) as well as teacher characteristics such as level of education, certification status, and years of professional experience, within-classroom percentage of ELL students, and percentage of special education students. Other level-1 coefficients (π1j - π 3j) are modeled as having fixed effects at level-2 while level-1 co-efficient π 4j is assumed to be affected by the intervention. The level-2 equations are shown as follows.
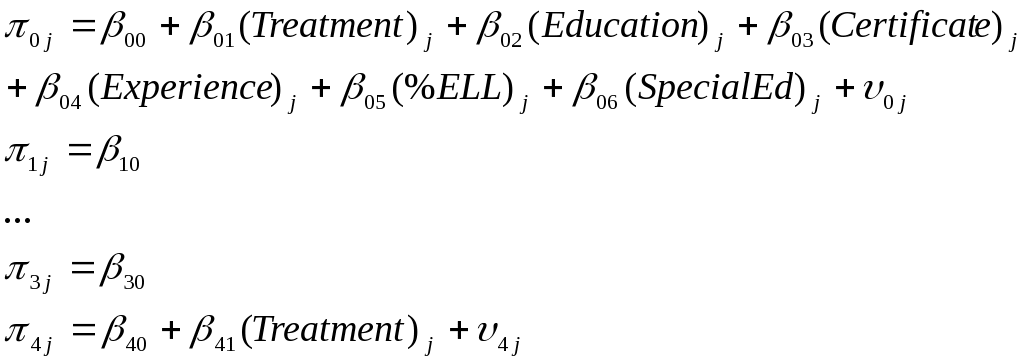
where
00 is the average student outcome measure across all teachers (i.e., grand mean);
(Treatment)j is an indicator variable for teacher j who received intervention: 1/2=Thinking Reader classes, and -1/2= control classes;
01 is the difference between the Thinking Reader teacher’s students and the comparison teacher’s students on average student outcome;
(Education)j is an indicator variable for whether teacher j received Master degree: 1=MA, and 0= BA;
02 is the effect of teacher education level on the student outcome measure;
(Certificate)j is a certification indicator variable for teacher j: 1=Yes, and 0= No;
03 is the effect of teacher certification on the student outcome measure;
(Experience)j is the measure of the teaching experience of teacher j;
04 is the effect of teaching experience on the student outcome measure;
(%ELL)j is the proportion of ELL students in the classrooms of teacher j;
05 is the effect of proportion of ELL students on the student outcome measure;
(%SpecialED)j is the proportion of special education students in the classrooms of teacher j;
06 is the effect of proportion of special education students on the student outcome measure; and
v0j is a random term associated with unmeasured effects on student outcome measure of teacher j.
41 is the effect of the intervention on the slope of Low Achieving subgroup.
Of primary interest among the level-2 coefficients is 01, which represents the intervention’s main effect on the outcome. A statistically significant positive value of 01 confirms the hypothesis that students of a teacher implementing Thinking Reader demonstrate better outcomes than their counterparts in the control teachers’ classrooms. The coefficient 41 shows whether Low Achieving students differ from other students in terms of the strength of association between Thinking Reader and the student outcome.
Missing data
Attrition from the sample can undermine the validity of a study, causing groups to be non-comparable on factors unrelated to the treatment. An intent-to-treat analysis is used to preserve the effects of the randomization procedure: i.e., “as randomized, as analyzed.” In this study, our unit of assignment is the teacher, and so an intent-to-treat analysis would require that we collect data from students whose teachers leave the study. We do not expect that teachers will decide to stop using the software mid-year, but teachers do leave for personal and professional reasons. We will train replacement teachers to use Thinking Reader, and keep track of which classrooms experienced this change. We recognize that we may have attrition at the student level, and so we will compute attrition rates (overall and between study groups) to monitor possible selection bias. Our intent-to-treat analyses will include baseline covariates to improve impact estimates. We will not impute outcome data because this will violate our intent-to-treat approach, but should there be missing pretest data from students who have been randomized into the conditions, we will use multiple imputation to generate plausible values for missing pretest data.
B2. Statistical Methods for Sample Selection and Degree of Accuracy Needed
In this section, we present power analyses for the Thinking Reader study. We assess the precision of impact estimate by computing the minimum detectable effect size (MDES) based on a multi-site cluster randomized design, in which teachers are randomly assigned within schools. Teachers are randomly assigned to treatment or control conditions, so clustering is assumed to take place at the teacher level, even though one teacher may teach more than one classroom.
The following assumptions are made in the power calculations:
Power: 80 percent.
Statistical significance: the statistical significance has been lowered to 0.0125, due to multiple comparisons (4 outcomes, simple Bonferroni corrections, two-tailed).
ICC = 0.15 between teachers.
R-square: three different values, for simplicity assumed to be the same for student, class, and school-level.
0.50
0.60
0.70
Three districts, total of 25 schools.
Each school is assumed to have 2 teachers; 4 classrooms. Each classroom includes 24 students. Power calculations were conducted assuming 80 percent response rates (i.e., about 19 students per classroom at the posttest)
Balanced allocation of teacher/classrooms in treatment and control conditions.
Schochet (2005) suggests three different approaches to calculating power for this type of a design. We believe that the formula for the case where schools are assumed as fixed effects is the most appropriate for our purposes. There will not be enough degrees of freedom with two teachers per school to estimate between-teacher effects within schools (which are confounded with between-school effects), unless we assume either (a) teacher variance equals zero, or (b) fixed school effects. Given the nature of the intervention and how it is delivered (reading software that complements teacher instruction), we consider teacher and classroom effects to be more important than differences between schools. The schools we are targeting are all urban, high need, and in districts that are in the same cluster defined by the state (as being similar in SES, demographics, etc.). Faced with a choice between assuming teacher variance as zero or fixed school effects, we decided that fixed school effects made more sense.
Here, the statistical formula in which schools are treated as fixed effects is used, but the fixed school effects are not included in the model. Then the between-classroom/teacher effect is estimated by combining classrooms across schools (in essence, ignoring school-level clustering):
![]()
Where
s is the total number of schools in the study sample;
k is the number of classrooms in each school;
![]() is
the average number of students per classroom (including 20 percent
attrition);
is
the average number of students per classroom (including 20 percent
attrition);
![]() is the unconditional
intra-class correlation (without covariates);
is the unconditional
intra-class correlation (without covariates);
![]() is the proportion of the
classroom-level variance component explained by the student-level
pretests;
is the proportion of the
classroom-level variance component explained by the student-level
pretests;
![]() is the proportion of the
student-level variance component explained by the student-level
pretests;
is the proportion of the
student-level variance component explained by the student-level
pretests;
M is
the multiplier that translates the standard error into a minimum
detectable effect
estimate. It is equal to the t
critical value for![]() ,
the significance level of the intended statistical test, plus the t
critical value for
,
the significance level of the intended statistical test, plus the t
critical value for![]() ,
the likelihood of detecting significant effects given a true effect
of a particular, size, i.e., the power of the test.
,
the likelihood of detecting significant effects given a true effect
of a particular, size, i.e., the power of the test.
If this approach is followed, the MDES estimates are 0.29, 0.26, and 0.22, for R-squared values of 0.50, 0.60, and 0.70, respectively.
These figures are well within the neighborhood of ES=0.29 that was reported by Dalton et al. (2002), in a small randomized controlled trial of Thinking Reader.4 This MDES range is consistent with meta-analyses conducted by Rosenshine and his colleagues, which suggest that the median effect sizes for the instructional techniques that underlie Thinking Reader are in the 0.30 range when standardized tests of reading comprehension are used as the outcome measures. Rosenshine & Meister (1994) report a median ES of 0.32 for the reciprocal teaching technique. Rosenshine et al. (1996) report a median ES of 0.36 for teaching students to generate questions.
We also conducted power analyses to address two additional considerations: (1) the inclusion of core curricula as strata, and (2) student subgroup analyses.
Including core curricula as strata impacts our data analyses much more than our statistical power. Although the statistical power of the study does not change, we have adjusted the degrees of freedom to acknowledge the strata (we assume five strata). If that is done, and using the same formula presented above, the MDES estimates remain the same: 0.29, 0.26, and 0.22, for R-squared values of 0.50, 0.60, and 0.70, respectively. If indicator variables for schools (but not treatment*school interaction terms) are included in addition to the strata (curricula) related variables, the MDES estimates are 0.30, 0.27 and 0.24, for R-squared values of 0.50, 0.60, and 0.70, respectively.
We recognize that subgroup analyses have far less statistical power. Below, we present results based on what we believe to be conservative assumptions. We did try to get more precise student demographic information from the CCD, based on school-level reports of disaggregated student achievement data (part of NCLB reporting requirements). But even though we know not all ELL and special education students end up getting tested, the numbers from the CCD seemed extraordinarily low. Therefore, we used the following numbers in our calculations:
Low achieving students: 5 for each teacher (across both her classrooms; i.e., with two teachers, 10 in the 6th grade/school);
ELL students: 3 for each teacher (6 in the 6th grade/school);
Special education students: 2 for each teacher (4 in the 6th grade/school).
The other assumptions used in the power calculations are the same as stated previously, as is the formula treating schools as fixed effects. Table 1 shows the estimates of MDES for different subgroups in the study. Again, we note that these are based on conservative assumptions, made in the absence of more precise school-level data. We believe that the numbers of students in these subgroups will be higher, so the MDES estimates presented in Table 2 paint a more pessimistic scenario than what we will actually observe.
Table
2.
MDES estimates for student subgroup analyses
|
R2 = 0.50 |
R2 = 0.60 |
R2 = 0.70 |
Low Achieving Students |
0.39 |
0.35 |
0.30 |
ELL Students |
0.45 |
0.40 |
0.35 |
Special Education Students |
0.52 |
0.47 |
0.40 |
B3. Procedures to Maximize Response Rates
Using the procedures described below, we expect a 100% response rate at the teacher level (the level of random assignment), and an 80% response rate at the student level.
A key feature of our recruitment strategy is providing, at no cost to the schools, the Thinking Reader materials. Tom Snyder Productions will install the Thinking Reader software, provide hard copies of the selected novels in sufficient quantity for all the treatment teachers’ classrooms prior to the onset of the intervention, and deliver free technical assistance by telephone during the school year. REL-NEI will provide supporting equipment (such as headphones for each student, and microphones if the computers available do not already have them built in). At the completion of the study, Tom Snyder Productions will install additional software and provide hard copies of the novels in sufficient quantity so that control teachers’ classrooms may use the program in the subsequent year. This injection of valuable resources to the schools should help our recruitment efforts.
To recruit schools, we will build upon EDC’s longstanding relationship with SEA and LEA technology and reading education leaders in the states. AIR will work with EDC’s Connecticut state liaison to identify the key persons to contact, then set up individual meetings with state, district, and school leaders, to promote interest in the study. Our experience in past evaluations has demonstrated the importance and value of building a consensus of support with schools. This leads to schools that have the capacity, willingness, and commitment to implement the intervention and to cooperate fully with the research and data collection procedures. Investing in site development at the front end reduces problems in the back end, helping to ensure smooth implementation of the evaluation.
Once districts have been identified, AIR will begin contacting schools. It is important to have clear, non-technical descriptions of the goals of the study, its methods, the roles and responsibilities of the various organizations involved, and the reasons to participate (see Attachment 4 for a study overview, as a PowerPoint presentation). Our past experience suggests that the research team must craft a message that leads with the benefits of participating and then is clear about the responsibilities assumed by participating schools, students, and by the research team. Schools that clearly understand the benefits of participating and the goals of the study are more likely to relate this to back to parents clearly. Furthermore, multiple conversations with potential sites are needed and final discussions are best held prior to the last month of the previous school year. We have found that the best recruitment strategy requires in-person discussion, especially when trying to explain to schools what participating in a random assignment study means and what their role in the study will be. Having that face-to-face contact is important for recruitment processes and will increase the likelihood that schools will participate and encourage their families to participate.
Families of students selected for the study classrooms will be sent an introductory letter and parental permission form (see drafts of these forms, Attachment 5). Only students who return the parental consent forms can participate in the evaluation, so it will be critical to get a high rate of return of these forms.
To obtain high response rates and high quality teacher- and student-level data the following
Clear parental consent forms that explain the purpose of the study and related data collection without jargon.
Clear explanation of study requirements to ensure that participating schools (both principals and teachers) fully understand the burden created by study participation;
Emphasizing the importance of participating in this evaluation, whose results are relevant not only for the participating classrooms, but potentially for all English/Language Arts classrooms with high percentages of striving readers.
Provide thorough training for the staff members who will be responsible for data collection regarding each instrument to guarantee high quality and consistency in data collection across classrooms and schools;
Assign a staff member(s) with experience with complex data collection to be a data manager. This person will be responsible for:
Building and maintaining good working relationship with the school districts and school personnel;
Scheduling data collection;
Overseeing and participating in data collection in person;
Use two sessions to administer the student-level tests to avoid testing fatigue;
Schedule an extra day for each data collection site-visit to account for last minute unexpected changes in school/teacher schedules. The extra day will also make possible testing students who were not in school during the originally scheduled test day.
B4. Tests of Procedures and Methods to Be Undertaken
In choosing the instruments, we drew heavily on standardized reading achievement tests and survey questionnaires that are either widely-used or have been used successfully in previous studies. Consequently, most of the survey questions have been thoroughly tested on large samples with prior OMB approval. Instruments and survey questionnaires are described below.
Gates MacGinitie Reading Tests. The Gates MacGinitie Reading Tests are well-established, widely-used standardized tests of reading achievement. Each test form consists of a vocabulary subtest and a comprehension subtest, designed to be administered at the same testing session. The vocabulary subtest measures reading vocabulary. Each target word is presented in a brief context that suggests the part of speech, and students are asked to select the word or phrase that most closely approximates the meaning of the test word. The comprehension subtest measures a student’s ability to read and understand different types of prose. Passages are excerpts from published books and periodicals, and represent materials that students may encounter in either academic tasks or during recreational reading. Students are asked a variety of questions, some of which tap into literal understanding of the text, while others require that the students make inferences or draw conclusions. The comprehension subtest also measures student ability to determine the meaning of words in an authentic context. The vocabulary subtest is approximately 20 minutes long, and the reading comprehension subtest is approximately 35 minutes long. (The Gates MacGinitie Reading Tests are assessments of ability/knowledge and are not included in our burden calculations.)
Reading Comprehension Strategy Survey for Students. We plan to measure students’ use of reading comprehension strategies with a self-report survey. The Metacognitive Awareness of Reading Strategy Inventory (MARSI; Mokhtari & Reichard, 2002) was selected. The developers found the reliability for the total sample was .89. At 6th grade, the Cronbach’s Alpha was .91. MARSI was subjected to multiple cycles of field-testing, validation and revision. Evidence suggests this is a valid measure that takes no more than 15 minutes to complete. We consulted with members of the REL-NEI Technical Working Group who provided input on the final selection of this measure. (The MARSI is an assessment of ability/knowledge and is not included in our burden calculations.)
Motivation for Reading Questionnaire. Students’ motivation to read will also be measured with a self-report survey. The Motivation for Reading Questionnaire (MRQ; Guthrie & Wigfield, 2000; Wigfield & Guthrie, 1997) is a well-known and widely used measure of reading motivation, and was developed to measure 11 possible dimensions of reading motivation. The reliabilities for the various subscales are not high, but a composite score based on 28 items of the MRQ has been used as an overall, robust measure of reading motivation, with an internal consistency of 0.85 (Guthrie, Wigfield, Metsala, & Cox, 1999). This survey typically requires 20 minutes to complete. (The MRQ is an assessment of ability/knowledge and is not included in our burden calculations.)
Brief Teacher Background Survey. A brief teacher background survey will be given to teachers. This survey will include questions such as years of experience, highest degree completed, and certification status, and is based on an instrument developed for the Teacher Knowledge of Instructional Processes Study, conducted by AIR for the National Center for Educational Statistics.
Classroom instruction. We propose sending field staff to visit a random subset of 24 teachers six times each year, so that we may gather information on how instruction, processes, and engagement differ between the Thinking Reader and the control group classrooms. We will schedule these visits to coincide with the treatment teachers’ coverage of each of the Thinking Reader novels, which will take place approximately December 2007 to April 2008. Twelve treatment teachers and 12 control teachers will be visited twice during each 4-week period that a Thinking Reader novel is covered.
We have selected the CIERA Classroom Observation Scheme (Taylor & Pearson, 2000) as a reliable, low-inference tool that can be used to document reading instruction in both the intervention and control classrooms. The measure documents seven parameters of the instructional environment: (1) who in the classroom is providing instruction and working with students; (2) the observed instructional groupings; (3) the major academic/social area being covered; (4) the materials used by the teacher and students; (5) the specific literacy activity; (6) the interaction style used by the teacher, and (7) the mode of student response.
The CIERA Classroom Observation Scheme protocol has been used in previous research and inter-rater reliability statistics between 0.92 and 0.95 are reported. The measure comes complete with a training manual, illustrative video clips and an additional practice video that can be used to attain reliability. These tools will help ensure the consistency of observer training. The protocol has been validated for grades 2-6 in a variety school districts, including several in Connecticut. These included high poverty districts (81% subsidized lunch) with diverse populations (20% ELL; 71% students of color) (Taylor & Pearson, 2005). (The classroom observations to be conducted using the CIERA protocol involve no questions of the teachers or students, and therefore not included in our burden calculations.)
Fidelity of treatment. The brief checklist that we plan to send biweekly to teachers in the treatment group is based on work that has been done by Dalton and her colleagues, in pilot studies of the Thinking Reader intervention. (The electronic student work logs that are automatically generated as part of the software’s operation and use are not included in our burden calculations.)
B5. Names of Statistical and Methodological Consultants and Data Collectors
The study, sponsored by the U.S. Department of Education, is being conducted through the Regional Education Laboratory – Northeast and the Islands (REL-NEI). Subcontractors to REL-NEI will carry out the study: the American Institutes for Research (AIR), Center for Applied Special Technology (CAST), and Sun Associates.
Table
3.
Key Study Staff
Name |
Role |
Organization |
Telephone Number |
Dr. Teresa Duncan |
Principal Investigator |
AIR |
(202) 403-6853 |
Dr. Bridget Dalton |
Director of Implementation |
CAST |
(781) 245-2212 x258 |
Dr. Katherine Drummond |
Study Director |
AIR |
(202) 403-5347 |
Dr. Yu Zhang |
Methodologist |
AIR |
(202) 403-5448 |
Dr. Anja Kurki |
Methodologist |
AIR |
(202) 403-5153 |
Dr. Jeff Sun |
Task Leader, Data Collection |
Sun Associates |
(978) 251-1600 x204 |
In addition to the persons listed above, members of the REL-NEI Technical Working Group (listed in Section A) provided substantial input to the study design.
1 Although the majority of students attending high-need schools may be struggling readers, we anticipate that a range of reading achievement will be represented in these classrooms. Thinking Reader is scaffolded so that students who are stronger readers may read with minimal or no support, or may choose to read the print version of the novel while still responding to the strategy prompts, completing the comprehension quick checks, and participating in the class discussions. Thinking Reader is designed to be responsive to individual differences, and was developed using principles of universal design for learning.
2 According to the Terms and Definitions document on the Connecticut State Department of Education website, “ERGs are a classification of the state’s public school districts into groups based on similar socio-economic status and need.” Factors that were considered in creating the ERGs were: family income, parental education, parental occupation, district poverty, family structure, home language, and district enrollment.
3 This excludes vocational, special education, and alternative/other schools.
4 The effect size of 0.29 was based on MANCOVA analyses, which adjusted for several covariates. A simple difference of differences computation produces an ES=0.41 for the same study.
| File Type | application/msword |
| Author | Courtney Zmach, Ph.D. |
| Last Modified By | DoED User |
| File Modified | 2007-07-10 |
| File Created | 2007-07-10 |
© 2025 OMB.report | Privacy Policy