Att_PD MATH OMB Part B 042007 7pm
Att_PD MATH OMB Part B 042007 7pm.doc
Impact Evaluation on Student Achievement of Teacher Professional Development In Mathematics
OMB: 1850-0816
STUDY OF THE IMPACT ON STUDENT ACHIEVEMENT OF TEACHER PROFESSIONAL DEVELOPMENT DESIGNED TO ENHANCE TEACHER CONTENT KNOWLEDGE AND PEDAGOGICAL CONTENT KNOWLEDGE IN MATHEMATICS
OMB Clearance Request, Part B
April 2007
Prepared for:
Institute of Education Sciences
United States Department of Education
Contract No. ED-04-CO-0025/0005
Prepared By:
American Institutes for Research®
Table of Contents
Page
Part B. Description of Statistical Methods 2
1. Respondent Universe and Sampling Methods 2
2. Procedures for Data Collection 7
3. Procedures to Maximize Response Rates 8
5. Names of Statistical and Methodological Consultants and Data Collectors 10
Appendix A Teacher Survey Fall 11
Appendix B Teacher Survey winter 12
Appendix C Teacher Survey Spring 13
Part B. Description of Statistical Methods
AIR and MDRC established the sample of participating districts by administering screening interviews across a pool of 120 districts and attempting to recruit approximately 24 eligible districts. These activities were approved by OMB in the first submission (OMB 1850-0816) and led to final agreements with 12 districts. Because the Mathematics PD Impact Study is not a program evaluation and does not employ random sampling of districts or schools for the sake of generalizability, these districts were screened and recruited on the basis of characteristics required by the study design. Districts were considered eligible for the study if they met all four of the following criteria:
Curriculum. One of the mathematics curricula of interest (Prentice Hall Mathematics, Glencoe McGraw- Hill Mathematics: Applications and Concepts or Connected Mathematics) was the primary mathematics curriculum for seventh grade in at least six middle schools.
Change in curriculum. The district had not recently changed its mathematics curriculum and did not anticipate a significant change in the next two years.
Duplicate treatment. The district was not already planning to provide professional development similar to that planned for the Mathematics PD Impact Study for seventh grade teachers.
Eligble schools. The district had at least four middle schools with two or more teachers of grade 7 mathematics, and with appromiximately one-third or more students in poverty.
An additional consideration in selecting the final sample of 12 districts was balance across curricula of interest. The final sample will include approximately equal numbers of districts using two contrasting curricula such that the sample embodies two sub-studies. One sub-study will be conducted in a set of districts using typical commercial texts, either Prentice Hall Mathematics or Glencoe McGraw-Hill Mathematics: Applications and Concepts; the parallel study will take place in a set of districts using a contrasting text, Connected Mathematics, which uses different instructional strategies. Each sub-study will include a sample of 42 schools drawn from six qualifying districts, located in several different states. Each sub-study will include six schools per district in three districts and eight schools per district in the other three districts to participate in the study. Within each district, the schools will be randomly assigned to the professional development treatment condition and the “business as usual” condition.1 This will yield 21 schools per condition within each parallel sub-study.
Having recruited the necessary schools, we are preparing to begin data collection in summer 2007. Project staff anticipate approximately three seventh-grade teachers per school, each teaching an average of three relevant2 seventh grade mathematics class sections with roughly 25 students per class section, i.e., 225 students per school, in a given academic year. Thus, the total universe of seventh grade teachers across the two sub-studies will be about 252; the total universe of students will be about 18,900. Testing will be restricted to random samples of students drawn from each of the teachers’ eligible classes in each school. Approximately 5 to 10 students will be drawn randomly from each class section, targeting an average of 60 students in each school. The total sample for each cycle of testing will be approximately 5,040 students (see Exhibit 2 for the complete structure of the design and Exhibit 3 for a summary of the sample sizes).
Exhibit 2. Study Design
District |
Mathematics Curriculum |
Treatment Group |
Number of Schools (unit of random-ization) |
Number of Teachers (based on estimate of 3 teachers per school) |
Number of Students in study classrooms (based on estimate of 25 students in each of three relevant class sections) |
Number of Students in assessment sample |
District 1 |
Prentice Hall or Glencoe |
Treatment |
4 |
12 |
900 |
240 |
Control |
4 |
12 |
900 |
240 |
||
District 2 |
Prentice Hall or Glencoe |
Treatment |
4 |
12 |
900 |
240 |
Control |
4 |
12 |
900 |
240 |
||
District 3 |
Prentice Hall or Glencoe |
Treatment |
4 |
12 |
900 |
240 |
Control |
4 |
12 |
900 |
240 |
||
District 4 |
Prentice Hall or Glencoe |
Treatment |
3 |
9 |
675 |
180 |
Control |
3 |
9 |
675 |
180 |
||
District 5 |
Prentice Hall or Glencoe |
Treatment |
3 |
9 |
675 |
180 |
Control |
3 |
9 |
675 |
180 |
||
District 6 |
Prentice Hall or Glencoe |
Treatment |
3 |
9 |
675 |
180 |
Control |
3 |
9 |
675 |
180 |
||
District 7 |
Connected Mathematics |
Treatment |
4 |
12 |
900 |
240 |
Control |
4 |
12 |
900 |
240 |
||
District 8 |
Connected Mathematics |
Treatment |
4 |
12 |
900 |
240 |
Control |
4 |
12 |
900 |
240 |
||
District 9 |
Connected Mathematics |
Treatment |
4 |
12 |
900 |
240 |
Control |
4 |
12 |
900 |
240 |
||
District 10 |
Connected Mathematics |
Treatment |
3 |
9 |
675 |
180 |
Control |
3 |
9 |
675 |
180 |
||
District 11 |
Connected Mathematics |
Treatment |
3 |
9 |
675 |
180 |
Control |
3 |
9 |
675 |
180 |
||
District 12 |
Connected Mathematics |
Treatment |
3 |
9 |
675 |
180 |
Control |
3 |
9 |
675 |
180 |
||
Total |
|
|
84 |
252 |
18,900 |
5,400 |
Exhibit 3. Sample Size by Treatment Group
-
Treatment Group
Number of Schools
Number of Teachers
Number of Students
Sub-study conducted within Prentice Hall or Glencoe Mathematics curricular context
Treatment
21
63
1,350
Control
21
63
1,350
Sub-study conducted within Connected Mathematics curricular context
Treatment
21
63
1,350
Control
21
63
1,350
Total
84
252
5,400
With the resulting design and conditions, the key comparison, treatment vs. “business as usual” (the control condition), can be examined in order to address the primary research question regarding the effects of professional development in mathematics on teacher instruction and student achievement separately within the context of each type of mathematics curriculum. In order to assess the statistical power of the study design, we used data from several large urban school districts from across the country to calculate the variance components and estimate Minimum Detectable Effect Sizes (MDES) for seventh grade mathematics achievement.3 Based on this analysis, Exhibit 4 presents estimates of how MDES for the estimated program effect on seventh grade achievement outcomes vary with different configurations of school and student sample sizes. These estimates confirm that, with the planned design parameters, the average estimated MDES fall within the target effect size range for the study. In particular, the first column of Exhibit 4 suggests that for an experiment involving 42 schools and 60 sampled students per school, the MDES is expected to be 0.20 standard deviations. Exhibit 4 also shows that if the samples from the two studies are combined for a total sample of 84 schools, the estimated MDES falls to 0.14 standard deviations. The statement of work in which ED specified the desired precision identified a target range for the MDES of 0.15 to 0.2 standard deviations.4 The estimated MDES of 0.20 for each sub-study and 0.14 for the combined sample suggest that precision for this study fits within this range.
Exhibit 4. Minimum Detectable Effect Sizes
Number of Schools |
Grade 7 Students Per School
|
|
||||
60 |
75 |
100 |
200 |
225 |
|
|
16 |
0.34 |
0.34 |
0.33 |
0.33 |
0.32 |
|
24 |
0.27 |
0.27 |
0.26 |
0.26 |
0.26 |
|
32 |
0.23 |
0.23 |
0.22 |
0.22 |
0.22 |
|
36 |
0.21 |
0.21 |
0.21 |
0.20 |
0.20 |
|
40 |
0.20 |
0.20 |
0.20 |
0.19 |
0.19 |
|
42 |
0.20 |
0.20 |
0.19 |
0.19 |
0.19 |
|
48 |
0.18 |
0.18 |
0.18 |
0.18 |
0.17 |
|
56 |
0.17 |
0.17 |
0.17 |
0.16 |
0.16 |
|
64 |
0.16 |
0.16 |
0.15 |
0.15 |
0.15 |
|
72 |
0.15 |
0.15 |
0.14 |
0.14 |
0.14 |
|
80 |
0.14 |
0.14 |
0.14 |
0.13 |
0.13 |
|
84 |
0.14 |
0.14 |
0.13 |
0.13 |
0.13 |
|
88 |
0.13 |
0.13 |
0.13 |
0.13 |
0.13 |
|
96 |
0.13 |
0.13 |
0.12 |
0.12 |
0.12 |
|
104 |
0.12 |
0.12 |
0.12 |
0.12 |
0.12 |
|
112 |
0.12 |
0.12 |
0.12 |
0.11 |
0.11 |
|
Data collection will be carried out by project staff at AIR, REDA International, MDRC and Westat. AIR will have overall responsibility for managing data collection and ensuring quality, coordination, and timeliness.
The following paragraphs describe the procedures to be used in collecting survey, inventory, and extant data. The data collection instruments to be cleared in this submission are included in a series of attached appendices. They include the Teacher Survey (fall, winter, and spring versions), the Teacher Knowledge Inventory (a secure instrument and therefore not attached), and the Extant Data Collection Protocol.
Teacher Surveys and Teacher Knowledge Inventory
REDA International will be responsible for administering all Teacher Surveys and Teacher Knowledge Inventories. The Teacher Surveys will be administered to all teachers by mail. The Teacher Knowledge Inventories will be administered to all teachers on site in proctored settings monitored by REDA staff. REDA will also convert responses from the these paper and pencil instruments into electronic files and produce public use datasets in accordance with the requirements of the U.S. Department of Education.
Extant Data Collection Protocol
Extant student data will be collected in the fall of each year, at the same time that students are rostered and sampled for achievement testing. The student test subcontractor will be responsible for this activity: they will compile rosters of eligible students at each participating school, incorporate requisite extant student data into the rosters, and apply simple sampling algorithms provided by AIR to create samples of approximately 60 students per school. All data for rostering will be requested in electronic form and will eventually be merged with the electronic Student Achievement Test records. Rostering and extant data collection will be updated in the spring of each year prior to the spring achievement testing.
The anticipated response rate is approximately 85 percent for each instrument and wave of data collection. These estimates are based on the previous experience of study staff in conducting the Study of PD Impact in Reading where survey response rates of 87% and over 90% were achieved for the Teacher Survey and the Teacher Knowledge Survey respectively. The following procedures will be used to ensure high response rates:
Obtaining high response rates depends in part on the quality of the instruments. See the next section for information on procedures designed to insure instrument quality.
Obtaining high response rates also depends in part of the length of the instruments. Each instrument for this study requires a brief time per administration. Teacher survey – Fall: 30 minutes, Teacher survey – Winter: 15 minutes, Teacher survey – Spring: 30 minutes, Teacher Knowledge Inventory: 45 minutes.
As part of the subcontract with REDA International, district coordinators employed by the study will be responsible for maintaining contact with respondents as well as garnering the support of school principals in an effort to track returns and follow up with non-respondents.
The Teacher Knowledge Inventory will be administered in-person and on site at professional development sessions or at the teachers’ schools to make completion of the TKI as convenient as possible.
The study will offer a social incentive to respondents by stressing the importance of the data collections as part of a high-profile study that will provide much-needed information to districts and schools.
Respondents in both the treatment and control groups will receive a small amount of compensation in return for participating in data collection activities. This is to make them feel that we value their time and participation thus encouraging them to participate and increasing the response rate.
The Teacher Survey has been pretested with small numbers of respondents (fewer than 10 respondents per instrument) and revised to ensure that the questions are clear and as simple as possible for respondents to complete. Pretest subjects included some teachers who had experienced the pilot version of our PD and other teachers whose experiences approximated our control condition. A think aloud, or cognitive lab format was used for pretesting, whereby each respondent was asked to complete the draft instrument, explain their thinking as they constructed their responses, and identify the following:
questions or response options that are difficult to understand;
questions in which none of the response options is an accurate description of their circumstance;
questions that call for a single response, but for which more than one of the options is an appropriate response;
terms that are not defined that should be defined; and
questions for which the information requested is unavailable.
The items for the Teacher Knowledge Inventory are undergoing rigorous internal review as well as external review by mathematicians consulting on the project. Each item is also being pretested using cognitive think aloud interviews with at least six middle grades mathematics teachers, to determine that each item is measuring the intended construct. In additon, to ensure that the instrument and procedures work effectively, and to verify preliminary estimates of the respondent burden and item difficulty, we are conducting a pilot in which intact forms of the Teacher Knowledge Inventory are tested under operational conditions (small group, proctored sessions). This pilot was discussed in the previous clearance request. Instruments and burden estimates will be revised using the pilot findings.
The Classroom Observation Protocol will be pretested by AIR staff in spring of 2007 to ensure that protocol procedures and items are working as designed. Following revisions to the instrument, classroom observers will be trained in the use of the protocol and will practice using the protocol in a combination of live and videotaped classroom settings.
Finally, the Extant Data Collection Protocol will be pretested in two districts, one of which participated in the pilot study, in order to ensure that the instrument and procedures work effectively.
This project is being conducted under contract to the Department of Education by AIR and MDRC. The instruments were developed by Michael Garet, Andrew Wayne, Fran Stancavage, James Taylor, Helen Duffy, and Suzannah Herrmann of AIR. Data collection will be carried out by project staff at REDA International, AIR, MDRC and Westat.
Appendix
A
Teacher Survey Fall
Appendix
B
Teacher Survey winter
Appendix
C
Teacher Survey Spring
Appendix D
classroom observation form
Appendix E
Extant Data Collection Protocol
1 Although it may not be feasible to include exactly the same number of schools per district in the evaluation sample, the study will approximate this objective as closely as possible.
2 The estimate of three teachers of seventh grade mathematics and three relevant class sections per teacher includes only those class sections eligible for the study. Eligible class sections are regular middle-track seventh grade mathematics class sections, thereby excluding advanced class sections such as gifted and talented programs and algebra courses as well as remedial class sections such as self-contained special education classes.
3 In particular, we used district-wide individual student databases from four recent school years in Houston, TX, Columbus, OH, Atlanta, GA and Newark, NJ in order to calculate the individual and school level parameters required to estimate minimum detectable effect sizes. These effects were calculated assuming “fixed effects” and the availability of both individual and school level prior achievement data. They were calculated using the equation:
MDES
=
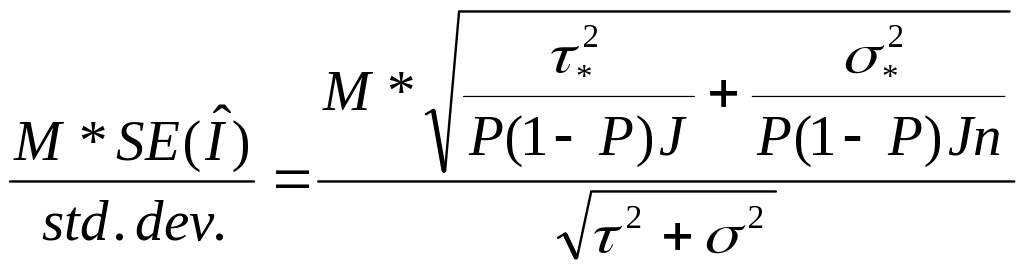 ,
where
,
where
M
= ![]() ,
and
is the multiplier that translates the standard error into a minimum
detectable effect estimate. It is equal to the t
critical value for
,
and
is the multiplier that translates the standard error into a minimum
detectable effect estimate. It is equal to the t
critical value for![]() ,
the
significance level of the intended statistical test, plus the t
critical value for
,
the
significance level of the intended statistical test, plus the t
critical value for![]() ,
the
likelihood of detecting significant effects given a true effect of a
particular, size, i.e., the power of the test.
,
the
likelihood of detecting significant effects given a true effect of a
particular, size, i.e., the power of the test.
![]() = the
school level variance component;
= the
school level variance component;
![]()
= the
school level variance, after controlling for whatever student or
school level characteristics are to be added to the impact
regression;
![]() = student
level variance of the outcome in question;
= student
level variance of the outcome in question;
![]() = student
level variance after controlling for student or school level
characteristics added to the regression;
= student
level variance after controlling for student or school level
characteristics added to the regression;
P= the proportion of treatment schools;
J = the total number of schools in the analysis;
n = the number of students within each school.
4 No absolute standard exists as to what represents a large versus a small effect size. Nevertheless, many researchers have relied on a rule of thumb that suggests that effect sizes of approximately 0.20 standard deviations or less be considered small, effect sizes of 0.50 be considered moderate, and effect sizes of 0.80 be considered large (Cohen, 1988). Further, a meta-analysis of treatment effectiveness studies by Lipsey (1990) found that, out of 102 studies, most of which were from education research, the vast majority found effects larger than the MDES implied by the design parameters of this study. In particular, the bottom third of the distribution of impacts ranged from about 0 to 0.32, the middle third of impacts ranged from 0.33 to 0.50, and the top third of impacts ranged from 0.56 to 1.26. Relevant studies focusing on teachers’ content knowledge reviewed by Kennedy (1998) obtained an effect size of 0.4 or larger for some outcomes – substantially greater than the 0.2 minimum detectable effect size target for our design, but with interventions of greater intensity and volunteer teachers. In short, prior research and our analysis of data across several large urban school districts suggest that the design parameters specified in the RFP are sufficient to detect policy-relevant effects should they exist.
| File Type | application/msword |
| File Title | STUDY OF THE IMPACT ON STUDENT ACHIEVEMENT OF TEACHER PROFESSIONAL DEVELOPMENT DESIGNED TO ENHANCE TEACHER CONTENT KNOWLEDGE AND |
| Author | American Institutes for Research |
| Last Modified By | DoED |
| File Modified | 2007-05-09 |
| File Created | 2007-05-09 |
© 2026 OMB.report | Privacy Policy