Att_PD MATH OMB Part A

Att_PD MATH OMB Part A.doc

Impact Evaluation on Student Achievement of Teacher Professional Development In Mathematics

OMB: 1850-0816

Document [doc]
Download: doc | pdf



STUDY OF THE IMPACT ON STUDENT ACHIEVEMENT OF TEACHER PROFESSIONAL DEVELOPMENT DESIGNED TO ENHANCE TEACHER CONTENT KNOWLEDGE AND PEDAGOGICAL CONTENT KNOWLEDGE IN MATHEMATICS



OMB Clearance Request, Part A





April 2007





Prepared for:

Institute of Education Sciences

United States Department of Education

Contract No. ED-04-CO-0025/0005


Prepared By:

American Institutes for Research®

Table of Contents

Page


list of exhibits


Page


Introduction



This is the second of a two-stage clearance request to carry out data collection activities for the Study of the Impact on Student Achievement of Teacher Professional Development to Enhance Teacher Content Knowledge and Pedagogical Content Knowledge in Mathematics (“Mathematics PD Impact Study”) . The purpose of the Mathematics PD Impact Study is to test a model of professional development that holds promise for improving middle school mathematics instruction and student achievement.

Last year, OMB approved the first clearance request, which described the study, the design, and two data collections that had to be completed prior to the study itself (OMB 1850-0816). These data collections included: 1) contacting a sample of districts and schools to establish their eligibility for the study and recruit them to participate in the full study, and 2) conducting a pilot test of a Teacher Knowledge Inventory (TKI) in the area of rational numbers in order to ensure that this critical outcome will be well measured in the full study.

In this second request, the Institute of Education Sciences (IES) of the U.S. Department of Education requests clearance for the study’s data collection instruments, specifically the Teacher Survey, Teacher Knowledge Inventory, and Extant Data Collection Protocol. Other data collections (e.g., forms completed by study staff, Student Achievement Tests) related to this study are included to provide a complete picture of the study.

This document contains three major sections. The first section is a full description of the Mathematics PD Impact Study, which provides context for the data collection instruments for which we are seeking clearance. The second section contains Parts A and B of the Supporting Statement for the Paperwork Reduction Act Submission. The final section (a set of appendices) contains the instruments for which we are requesting clearance.

Description of the Mathematics PD Impact Study

Purpose

IES and its contractors have designed a randomized field trial, hereafter referred to as the Mathematics PD Impact Study, to examine the impact of professional development on teacher knowledge, instruction and student achievement in mathematics. This study will examine two experimental conditions:

  • Treatment: A professional development intervention consisting of a three-day summer institute (18 hours per teacher), five one-day seminars held during the school year (30 hours per teacher), and 10 days of intensive in-school coaching (20 hours per teacher)

  • Control: A “business as usual” condition within the same districts where teachers receive the mathematics professional development that is typically covered, absent our intervention.

The study will focus on grade 7 mathematics teachers, and the treatment will focus on the critical domain of rational numbers (i.e., fractions, percents, decimals, and proportional reasoning). Mastery of rational numbers is an essential foundation for algebra, and rational numbers account for a significant percentage of grade 7 mathematics content in all states.

The Mathematics PD Impact Study is actually two parallel sub-studies of the same design conducted in two different , but widely used curricular contexts. The two curricula cover essentially the same mathematics content, but represent contrasting instructional approaches and consequently make somewhat different demands on teachers’ skills.

A pilot test of the professional development intervention is being conducted during the 2006-07 school year. Draft data collection instruments are also being piloted with less than 10 respondents. Purposive samples of districts using each of the two predetermined curricula are being recruited for the full study during the 2006-2007 school year. The professional development intervention will be implemented during the summer of 2007 and the 2007-08 school year, and data will be collected on the implementation and impact of the intervention from the summer of 2007 until the spring of 2009. To ensure objectivity, the study will be carried out by two teams. One team selected the professional development intervention and manages its implementation at the sites recruited for the study, and a separate team leads the data collection and analysis of the effects of the professional development intervention.



Research Questions

The proposed study focuses on one central research question:

  1. What are the impacts on teacher knowledge, teacher practice, and student mathematics achievement of providing teachers with intensive professional development in the area of rational numbers?

In addition, attention will be given to the following supplementary questions:

  1. Is the mathematics professional development intervention implemented with fidelity (treatment only)?


  1. To what extent do teachers (both treatment and control) participate in mathematics professional development activities?


  1. To what extent is the amount of teacher participation in the professional development intervention related to changes in teacher practice and student learning?


  1. What is the relationship between teacher experience or prior knowledge and the impacts of the professional development intervention?

  2. What is the relationship between student characteristics and the impacts of the professional development intervention?

  3. Do the impacts of the professional development intervention change over time?

  4. Of practical importance to administrators, what are the per teacher costs of participating in this type of professional development?


Treatment Selection and Characteristics

The professional development model at the core of this study has been developed through an extensive review of the literature, where there is concurrence regarding three core features and three structural features of professional development that show strong associations with changes in teacher practice. The three key structural features include:

  1. duration of the activity (Garet et al., 2001; Cohen & Hill, 2001; and O’Connor, 1999);

  2. form of the activity, how professional development activities are organized (Garet et al., 2001; Hargreaves & Fullan, 1992; Little, 1993; and Stiles, Loucks-Horsley, & Hewson, 1996); and

  3. collective participation of groups of teachers (Ball, 1996; Knapp, 1997; Talbert & McLaughlin, 1993; Elmore, 2002).

The three key core features include:

  1. a focus on the content teachers teach (Cohen & Hill, 2001; Garet et al., 2001; Kennedy, 1998; Carpenter, Fennema, et al., 1989);

  2. opportunities for teachers to learn actively and connect their learning to practice (Garet et al., 2001; Lieberman, 1996; Loucks-Horsley et al., 1998); and

  3. coherence among professional development goals, teachers’ own goals, and the standards and assessments that should guide teachers’ practice (Cohen & Hill, 1998; Garet et al., 2001; Grant, Peterson & Shojgreen-Downer, 1996; Lieberman & McLaughlin, 1992).

Exhibit 1 depicts a conceptual model of the key features of this study’s professional development treatment as well as the intended outcomes of the study.







Exhibit 1. Conceptual Model




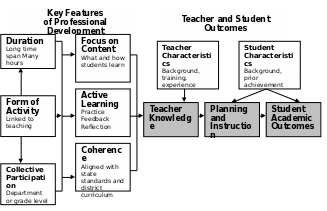
The providers who will deliver the professional develpoment were selected through a competitive process in April 2006. The providers—America’s Choice and Pearson Achievement Solutions—and the study’s implementation team have now piloted and refined the professional development. As summarized in Exhibit 2, the professional development includes intensive, content-based summer institutes, follow-up seminars, and ongoing coaching during the school year.



Exhibit 2. Summary of Treatment

Professional Development Activities

Treatment

Summer Institute for teachers

18 hours

Seminars during the school year

30 hours (5 days)

On-site coaching during the school year

20 hours per teacher (10 days per school)

Total per teacher, 2007-08

68 hours




Data Collections

In this second request, IES requests clearance for the full study’s data collection instruments, specifically the Teacher Survey, Teacher Knowledge Inventory, and Extant Data Collection Protocol. Other data collections (e.g., forms completed by study staff, Student Achievement Tests) related to this study are included to provide a complete picture of the study.



The data collections for the PD Mathematics Impact Study serve three broad purposes:

  1. Documenting the implementation of the two interventions, both to verify the fidelity with which the models were implemented and to produce a description of the interventions that will allow others to replicate them.


  1. Assembling contextual data to help understand the results:

  • data to describe the sample of schools and teachers

  • data to compare treatment and control schools and teachers prior to implementing the treatment (i.e., to assess how well randomization has balanced the samples)

  • covariates (control variables) that can be included in analyses to reduce unexplained variance

  • variables that may interact with the treatment


  1. Measuring the outcomes, including teacher knowledge, teacher practice, and student achievement (see Exhibit 1).


An overview of the study’s instruments, their primary purposes, and the schedule for their use is provided in Exhibit 3. The bolded instruments involve burden and are therefore the basis for seeking clearance. The unbolded instruments are listed to provide a complete picture of the study.

As the table shows, several of the instruments will be administered more than once during the study. This is important for two reasons: (1) to measure changes in the outcome measures over time and (2) to document contextual and treatment data within a timeframe that can be easily recalled by respondents. Data collection instruments will only be administered multiple times when necessary for one of these reasons.

Note that the table does not include two activities for which clearance has already been received: (1) district screening and recruitment and (2) the pilot of the Teacher Knowledge Inventory. District screening and recruitment are complete.


Exhibit 3. Summary of Data Collection Instruments and Schedule

Primary Purpose
Data Collection Instrument

Data Collection Schedule

Document Treatment

Provide Screen/ Context/ Covariates

Measure Outcomes

Fall 2006 and Winter 2007

Spring 2007

Summer 2007

Fall

2007

Winter 2008

Spring 2008

Summer 2008

Fall

2008

Winter 2009

Spring 2009

Summer 2009

X



1. Institute/Seminar Documentation Protocols:

--PD Observation Form

--Training Sign-in Sheet

--PD Evaluation Form: Teacher Reflections



X

X

X

X





 

X



2. Coach Log of Coaching Activities




X

X

X





 

X

X


3. Teacher Survey




X

X

X


X

X

X

 


X

X

4. Teacher Knowledge Inventory



X



X




X

 



X

5. Classroom Observation Form






X



X


 


X

X

6. Student Achievement Test 7th grade

(Student Achievement Test 8th grade)




X


X


X


X

X(option)



X

X

7. Extant Data Collection Protocol



X



X

X



X

X

Institute and Seminar Documentation Protocols

Row 1 of Exhibit 3 describes the forms that will be used to document the delivery of the intervention and the participation of each teacher in the intervention. These instruments are listed in order to give a broader overview of the data that the study will have available for analysis. In each of the twelve districts, the treatment teachers will receive their professional development in a 3-day summer institute followed by 5 days of seminars during the ensuing school year. These professional development days will be documented using two observation forms that are designed to measure the fidelity with which the planned institute and seminar programs are implemented in each district. AIR study staff will document adherence to/departures from each day’s presentation schedule and will rate the quality of presentation and participants’ involvement on a standardized PD Observation Form. In addition, participants will provide evidence of their hours of exposure to the PD program by signing a Training Sign-in Sheet twice during each professional development day. Teachers will also complete end-of-day, end-of-institute, and end-of-seminar Teacher Reflections Forms. These are typically provided as part of district professional development. Although the primary purpose of these reflections will be to provide the presenters with rapid feedback on teachers’ comprehension, confusions, and desire for additional information, the evaluation team will summarize the responses as one type of evidence about the participants’ assessment of the professional development they have received.



Coaching Documentation Protocols

Row 2 of Exhibit 3 shows the Coach Log of Coaching Activities, which will be used to document the delivery of the cooaching component of the intervention. This information will be used to gain a picture of the amount and type of coaching in which each individual teacher participated. The instrument is not included because the coach is an employee of the study.



Teacher Survey

Row 3 of Exhibit 3 highlights the Teacher Survey, a written questionnaire that will be used to collect information on their mathematics teaching experience, their course assignments, chapters covered, and their training. This survey will be administered in both the treatment and follow-up years during the fall, winter and spring. To reduce the length of each survey administration as much as possible, teachers will report on their teaching background only on the first fall survey. They will report on their course assignments on the fall forms for each year, and they will update the information on their most recent training on each survey.

The primary purpose of the teacher background module on the Fall 2007 Teacher Survey is to collect data that will (1) enable comparisons between the sample teachers and national population of teachers, (2) enable comparisons between the treatment and controls prior to intervention, and (3) provide covariate and interaction variables for the impact analyses. (An example of a factor that might prove to interact with the treatment is the teacher’s previous training—e.g., teachers with less prior training related to mathematics instruction might show greater gains in knowledge and greater changes in certain instructional strategies than teachers with substantial training similar to that offered by the intervention.)

Given that the mathematics performance of seventh grade students at end of the school year is the primary outcome of interest to the study, the main purpose of the classroom context module on the Fall 2007 and Fall 2008 forms is to enable comparisons between treatment and control classrooms and to identify possible covariates and interaction variables for the impact analysis. It should be noted that some aspects of classroom context will be investigated prior to randomization. For instance, some methods of organizing mathematics instruction, such as the use of mixed-grade mathematics classes, would unduly complicate the analysis, and an attempt will be made to eliminate such cases from the study prior to randomization. However, the classroom context questions on this survey will ensure that we are aware of cases that may not have been appropriately eliminated.

Each administration of the Teacher Survey also will be used to gather information about the full set of professional development activities experienced by both treatment and control teachers over several months prior to each survey administration, allowing teachers to recall more recent events and complete shorter forms at each administration. The main purposes of this fine-grained examination of teachers’ experiences are to assess (1) the magnitude of the contrast between the background level of professional development (including coaching) experienced by teachers in each district and the level experienced by teachers in the experimental treatment and (2) differences among treatment teachers in the treatment “dosage” they experience , which could occur due to possible variations in program implementation or individual attendance.

Each winter and spring form of the Teacher Survey contains an item on chapter coverage to detect possible differences in the amount of time spent by treatment and control teachers on chapters addressing rational numbers. The professional development is not designed to affect time spent on these chapters, but it will be important to have data to rule out the possibility that any observed effects on student achievement can be attributed to additional time spent on rational numbers topics. Each winter and spring form currently shows three items on chapter coverage – one for each of the three of the textsbooks in use in participating districts—and will be customized before administration to include only the applicable item.

The fall, winter, and spring forms of the Teacher Survey are included in Appendices B, C, and D.



Teacher Knowledge Inventory

Row 4 indicates the assessment instrument that will be used to collect outcome information on changes in teachers’ knowledge. This instrument will be the final version of the Teacher Knowledge Inventory (TKI), which OMB gave clearance for pilot testing last year. The TKI will be administered to treatment and control teachers three times over the course of the study: in summer 2007, in spring 2008, and spring 2009. The TKI is designed to be administered in 45 minutes.

The TKI will consist of three parallel forms, each comprising 24 items. The items will be divided equally between common content knowledge (CCK) and pedagogical content knowledge (PCK), and they will also be distributed evenly across 12 key understandings, 6 in the general area of fractions and decimals (FD1-6) and 6 in the general area of ratios, proportions, and percents (RPP1-6). Thus, each form will exhibit the distribution of items depicted in Exhibit 4.

Exhibit 4. Teacher Knowledge Inventory Item Distribution

Type of item


Key Understanding

Common Content Knowledge (CCK)

Pedagogical Content Knowledge (PCK)

Total

Fractions and decimals




FD1

1

1

2

FD2

1

1

2

FD3

1

1

2

FD4

1

1

2

FD5

1

1

2

FD6

1

1

2

Ratio, proportion, and percent




RPP1

1

1

2

RPP2

1

1

2

RPP3

1

1

2

RPP4

1

1

2

RPP5

1

1

2

RPP6

1

1

2

Total

12

12

24



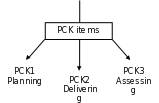
Each CCK item will require conceptual understanding related to a specific key understanding. Each PCK item will address both a specific key understanding and a specific pedagogical skill. Allowable pedagogical skills are classified under three aspects of instruction: planning instruction, delivering instruction, and assessing understanding. Across the three forms, each key understanding will be paired once with each aspect of instruction, and each form of the TKI will exhibit a balance across the three aspects of instruction as depicted in Exhibit 5.



Exhibit 5. Distribution of Items within Each Key Understanding

Key Understanding



















All PCK items will be multiple choice. CCK items will be equally divided between multiple choice items and short constructed response items, but only CCK items with numeric solutions will be candidates for constructed response.



Classroom Observation Form

Differences in the instructional practices of the treatment group and control group teachers will be assessed by using the Classroom Observation Form, as indicated in Row 5 of Exhibit 3. Observations will be conducted during the 2007-08 and the 2008-09 school years. One observation per teacher will be conducted for each school year. Approximately 252 teachers will be observed for a total of approximately 504 classroom observations. The length of each observation will be one class session that can last from 45 to 90 minutes. Comprehensive training of observers will be conducted by AIR staff prior to the 2007-08 and 2008-09 school years. Lead observers will conduct new observer orientations and reinforcement sessions as needed.

The Classroom Observation Form is intended to measure only a few key dimensions of classroom instruction. These dimensions are the variables most relevant to this intervention and therefore most likely to be helpful in interpreting the mechanism through which the PD Math intervention may exert an effect on student learning. The observation instrument is based on those developed for evaluations such as the TIMMS Video study (Hiebert et al., 2003), Cognitively Guided Instruction Study (Carpenter et al., 1989), and the QUASAR project (Silver and Stein, 1996). More specifically, the use of teacher instructional practices will be observed along the following dimensions: 1) clarity and grounding of lesson focus; 2) lesson planning and anticipation of student needs involving responses, errors, and misconceptions regarding mathematical procedures and concepts; 3) explanations, answers, and feedback to students; 4) questioning and examination of student work to assess student understanding; 5) use of materials and representations of mathematical concepts and procedures in the lesson; and 6) student engagement. This form will be filled out by study staff and is described here for the purpose of providing a full picture of the scope of the study.


Student Achievement Test

Students’ performance on assessments of their knowledge and skill in the domain of rational numbers at the end of seventh grade is the ultimate outcome of interest to the study. Row 6 of Exhibit 3 indicates the assessment instrument that will be used to collect information on this critical outcome. The Student Achievement Test will be administered to a sample of students in grade 7 classes taught by participating teachers. It will also be administered in grade 7 classes taught by those teachers in the year following the professional development, to determine whether any impact of the intervention on teachers’ effectiveness is sustained. During each of those years, the test will be administered in both the fall and spring, with the fall test score serving as a pretest covariate. Note that the X marked as optional in row 6 indicate the possibility of collecting spring eighth grade test data on the students who were 7th graders during the intervention year.

We describe the nature of the Student Achievement Test below to provide a more complete picture of the study. The student rational numbers knowledge test, which is designed to be administered within a single class period of 45 minutes, is a computer‑based adaptive test developed by the Northwest Evaluation Association (NWEA). The test platform on which our custom test will run is well tested and in widespread use by school districts nationwide. The test items have been previously field tested and validated as well as reviewed for quality by mathematicians consulting on the project.

The content of the test aligns with the content of the professional development treatment. The 30 test items per form will be distributed equally between 1) decimals and fractions, and 2) percents, ratios, and proportions and will produce separate subscales for each of these domains. Within decimals and fractions the test will place relatively more emphasis on fractions than decimals in order to reflect the actual relative emphasis on these topics in the curricula in use and current state standards documents. With these goals in mind, during each administration each student will see 30 items distributed across subgoals as depicted below in Exhibit 6.


Exhibit 6. Distribution of Student Knowledge Assessment Items Across Subgoals Within One Student for One Test Administration

Fractions

Decimals

Ratio, Proportion, and Percent

Concepts

1a. Concepts of Fractions    


3

2a. Concepts of Decimals


2

3a. Concepts of Percent, Ratio, and Proportion

5

Operations

1b. Operations with Fractions


3

2b. Operations with Decimals


2

3b. Operations with Percents, Ratios and Proportions

5

Problem Solving

1c. Solve Applied Problems Involving Fractions

3

2c. Solve Applied Problems Involving Decimals

2

3c. Solve Applied Problems: Percent, Ratio, Proportion

5


Total Fractions Items


9

Total Decimals Items


6

Total Percent, Ratio, Proportion Items

15





Extant Data Collection Protocol

Finally, row 7 of Exhibit 3 refers to data collection protocols that will be used to collect rostering data needed for sampling of students and demographic information for students of participating teachers. These data will be collected by the test administration subcontractor before each test administration—that is, just prior to the start of the school year and again in the early spring—in the form of electronic files from participating schools (or districts if possible). The student data include school and teacher/classroom identifiers, birth month/year, gender, race/ethnicity (current U.S. census categories), days absent (up to rostering date), school lunch program status, English language status, Individualized Education Plan status, and gifted and talented program status. Each summer, the subcontractor will also collect the previous spring’s state accountability mathematics test results for each participating student. State tests are not as well aligned with the professional development as the Student Achievement Test described earlier. However, the state test data have the greatest policy relevance and may reveal that the professional development affected achievement in topics outside of rational numbers. See Appendix E for a copy of the protocol.

Supporting Statement for Paperwork Reduction Act Submission

  1. Justification

  1. Circumstances Making Collection of Information Necessary

The No Child Left Behind (NCLB) legislation sent a message that the federal government seeks to improve the quality of schooling in the United States for all students. Good teachers, of course, are critical to the improvement of schooling and student achievement (ECS, 2003; Rowan, 2002; Sanders & Rivers, 1996; Whitehurst, 2002). NCLB recognizes this point, as evidenced by the Title I requirement that every child have “highly qualified” teachers and the requirement that states report the percentage of their teachers participating in high-quality professional development. Title II places heavy emphasis on achieving this goal by seeking to improve both pre-service and in-service professional development. School districts and states receive nearly $3 billion in federal Title II, Part A funds which they may use for a wide range of activities, including providing professional development to improve the knowledge of teachers. The law stipulates that these funds be used for professional development activities that advance teacher understanding of effective instructional strategies that are based on scientifically based research and that improve student academic achievement or substantially increase the knowledge and teaching skills of teachers [Title IX, Part A, Section 9101(34)].

Many states and districts have also recognized the importance of professional development and have launched ambitious initiatives to upgrade the knowledge and skills of their teachers. However, without studies such as the Mathematics PD Impact Study, states and districts have little scientific research on which to base their decisions about where their professional development dollars should be spent. The Mathematics PD Impact Study examines the impact of a strong model of teacher professional development that includes intensive, content-based summer institutes, follow-up seminars, and ongoing coaching during the school year. The professional development will be delivered by two providers—America’s Choice and Pearson Achievement Solutions—selected through a competitive process.



The Mathematics PD Impact Study is aligned with the larger goals of NCLB in two ways. First, it is one of the first rigorous, large-scale studies of the impact of professional development. Second, because it is the intention of the Department of Education to focus on the effectiveness of professional development for improving the mathematics achievement of students in high-poverty schools, it aligns with the interest of NCLB in improving the academic achievement of students in such schools.


  1. Purposes and Uses of the Data

The purpose of the Mathematics PD Impact Study is to test a model of professional development that holds promise for improving middle school mathematics instruction and student achievement. The success of several federal programs (e.g., Title I, Title II) relies on the selection of effective professional development strategies, and current studies of professional development interventions do not provide significant guidance in middle school mathematics. Therefore, the Institute of Education Sciences (IES) of the U.S. Department of Education has commissioned the Mathematics PD Impact Study to evaluate whether a comprehensive content-based in-service professional development program—following the model given earlier and depicted in Exhibit 1—can substantially improve middle school mathematics instruction and thereby improve students’ mathematics achievement. Data collected by the Mathematics PD Impact Study will be of immediate interest and import for policymakers, researchers, and practitioners.



  1. Use of Technology to Reduce Burden

The use of technology will differ by instrument. The Teacher Survey and the Teacher Knowledge Inventory will be administered using pencil and paper questionnaires. The Teacher Survey will be administered by mail, and the Teacher Knowledge Survey will be administered in person and proctored by study staff. Proctoring the Teacher Knowledge Survey will allow us to verify that the teachers have completed the instrument without consulting reference materials or peers, and will ensure that teachers receive, complete, and return the instrument in a timely manner.

The Student Achievement Test will be administered via computer and will adapt to individual student performance levels during the test. The use of a computer-adaptive test reduces the time needed to obtain good measures of student performance and will therefore minimize the study’s disruption of instructional time.

The Extant Data Collection Protocol will make use of electronic database technology and secure email communications to the maximum extent possible. Ideally, district-wide data base reports will be accessed so that there will be no burden on individual schools.



  1. Efforts to Identify Duplication

Although NCES collects sample survey data on teacher participation in professional development, it is descriptive and does not permit analyses of impact. The Mathematics PD Impact Study is one of very few rigorous impact studies of professional development currently underway, and it is distinguished further by its focus on mathematics.

The possibility of linking to existing data rather than collecting new information was investigated for each instrument, and in no case were there adequate alternative sources of information. Regarding student achievement, we determined that state tests were not sufficently aligned to the intervention, which focuses on rational numbers content. Furthermore, a review of several state frameworks and test blueprints revealed substantial state variation in the percentage of items that focus on rational numbers (e.g., 23% of 7th grade items in Texas and 41% of 7th grade items in Connecticut).



  1. Methods to Minimize Burden on Small Entities

No small businesses or entities will be involved as respondents.



  1. Consequences of Not Collecting the Data

The Mathematics PD Impact Study represents the first effort by the Department of Education to conduct a rigorous study of the effects of professional development in mathematics. As required by NCLB, states must adopt professional development that is grounded in scientifically based research. Without this study, states and districts will have a limited basis on which to comply.



  1. Special Circumstances

No special circumstances apply to this study.



  1. Federal Register Comments and Persons Consulted Outside
    the Agency

The 60-day notice for this collection was published on Feb. 23, 2007 on page 8153, vol. 72. No public comments were received.

To assist with the development of the screening criteria and the study as a whole, project staff have drawn on the experience and expertise of a network of outside experts. The consultants and their affiliations are listed in Exhibit 7.

Exhibit 7. Project Advisor, Project Consultants, and Technical Working Group Members

Project Advisor

Expert

Affiliation

Andy Porter

Patricia and Rodes Hart Professor of Educational Leadership and Policy, and Director of the Learning Sciences Institute at Vanderbilt University


Project Consultants

Expert

Affiliation

Mark Hoover Thames

Research Scientist, Learning Mathematics for Teaching Project, University of Michigan

Sybilla Beckmann

Professor, University of Georgia

Jim Lewis

Professor, University of Nebraska

Cathy Brown

Independent Consultant


Technical Working Group Members

Expert

Affiliation

Julian Betts

Professor of Economics, University of California-San Diego

Doug Carnine

Director, National Center to Improve the Tools of Educators, University of Oregon

Mark Dynarski

Senior Research Fellow, Mathematica Policy Research

Lynn Fuchs

Professor, Department of Special Education, Vanderbilt University

Russell Gersten

Professor Emeritus in the College of Education, University of Oregon

Kenneth Koedinger

Associate Professor, Carnegie Mellon University

Brian Rowan

Professor, University of Michigan

John Woodward

Professor of Education, University of Puget Sound

Hung-Hsi Wu

Professor of Mathematics, UC Berkeley



To date, the project advisor and Technical Working Group (TWG) members have convened twice. In October 2005, TWG members provided comments on the study design, the treatments, and the data collection instruments. An additional meeting was held in March, 2007 to provide final review of the study design and the instruments. Subsequent meetings will be held in spring 2009 and spring 2010 to solicit feedback on the study reports. Project staff also use outside experts individually for consultation on an as-needed basis.









  1. Payment or Gifts

Incentives are planned for the Teacher Survey, Teacher Knowledge Inventory, and Classroom Observation Forms. The proposed incentive amounts are based on experience in a similar study—the Study of Professional Development Impact in Reading. The amounts never exceed those proposed in the NCEE memo Guidelines for Incentives for NCEE Evaluation Studies, dated March 22, 2005.

The Fall and Spring Teacher Surveys each require 30 minutes to complete and are therefore considered high-burden teacher surveys. They are administered by mail, and high response rates are needed from both the treatment and control group. The planned incentive amounts is $30 for each instrument, which proved sufficent for similar instruments in the Study of Professional Development Impact in Reading.

The Winter Teacher Survey requires 15 minutes to complete and is also administered by mail. We plan a $15 incentive for each administration, which is consistent with the guidelines in the NCEE memo. Despite requiring little time, the survey is one of three that will be administered each year. It is very important for the study to maintain participants’ cooperation with all data collections for the entire course of the study.

The Teacher Knowledge Inventory is an assessment. It requires a higher incentive rate in order to account for the potential resistance to being rated and to account for respondents’ fears that information will be misused. The Teacher Knowledge Inventory requires 45 minutes and therefore is considered a medium-to-high burden assessment. Because it is administered in person, the incentive amount can be lower than the amount of $75 recommended in the NCEE memo. A similar instrument administered in-person in the Study of Professional Development Impact in Reading required 30 minutes, and an incentive of $30 was sufficient. We plan an incentive of $50 to account for the additional time required (45 minutes).

The Classroom Observation Form is also an assessment but poses significantly lower burden than the Teacher Knowledge Inventory, because teachers are observed doing what they would normally do. The NCEE memo recommends an incentive of $25 per observation, and that amount was used successfully in the Study of Professional Development Impact in Reading. The planned incentive is $25 per observation.

Note that no payments will be given to district or school administrators for the completion of the Extant Data Collection Protocol.



Exhibit 8. Schedule of Incentives for Participation in Data Collections

Data Collection Activity

Schedule/Payment

Summer 2007

Fall /Winter2007

Spring 2008

Fall /Winter2008

Spring 2009

Teacher Survey - Fall

$30

$30

Teacher Survey – Winter

$15

$15

Teacher Survey – Spring

$30

$30

Teacher Knowledge Inventory

$50

$50

$50

Classroom Observations

$25

$25

$25

$25



  1. Assurances of Confidentiality

The Education Sciences Reform Act of 2002, Title I, Part E, Section 183 requires "All collection, maintenance, use, and wide dissemination of data by the Institute" to "conform with the requirements of section 552 of title 5, United States Code, the confidentiality standards of subsection (c) of this section, and sections 444 and 445 of the General Education Provision Act (20 U.S.C. 1232g, 1232h)." These citations refer to the Privacy Act, the Family Educational Rights and Privacy Act, and the Protection of Pupil Rights Amendment.

In addition for student information, "The Director shall ensure that all individually identifiable information about students, their academic achievements, their families, and information with respect to individual schools, shall remain confidential in accordance with section 552a of title 5, United States Code, the confidentiality standards of subsection (c) of this section, and sections 444 and 445 of the General Education Provision Act.

Subsection (c) of section 183 referenced above requires the Director of IES to "develop and enforce standards designed to protect the confidentiality of persons in the collection, reporting, and publication of data.”

Subsection (d) of section 183 prohibits disclosure of individually identifiable information as well as making the publishing or communicating of individually identifiable information by employees or staff a felony.

AIR, MDRC, REDA International, and the student test administration contractor will all protect the confidentiality of all information collected for the study and will use it for research purposes only. No information that identifies any study participant will be released. Information from participating teachers and students will be presented at aggregate levels, by treatment condition, in reports. Information on students will be linked to their teachers, and information on teachers will, in turn be linked to their schools and districts, but neither students nor teachers will be linked to any individually identifiable information. No individually identifiable information will be maintained by the study team. All members of the study team having access to the district-level data have been certified by AIR's Institutional Review Board (IRB) as having received training in the importance of confidentiality and data security. All district-level identifiable information will be kept in secured locations and identifiers will be destroyed as soon as they are no longer required. 



  1. Justification of Sensitive Questions

No questions of a sensitive nature will be included in the Teacher Survey or Teacher Knowledge Inventory.



  1. Estimates of Hour Burden

The total estimated annual hour burden for the data collections for the Mathematics PD Impact Study is 1,492 hours. Exhibit 9 summarizes the estimates of respondent burden for study activities. The burden estimate for the Teacher Survey includes time for 85 percent of all 252 teachers (treatment and control) in the 12 districts to respond to a 30-minute survey in the fall, a 15-minute survey in the winter , and a 30-minute survey in the spring in each of the two years of the study. The burden estimate for the Teacher Knowledge Inventory includes time for the same treatment and control teachers to complete three 45-minute assessments. The averaged burden estimate for district or school staff to complete the Extant Data Collection Protocol includes time for all 84 schools in 12 districts to read the request, participate in a follow-up phone call, locate and submit the required data files.



Exhibit 9. Hour Burden for Respondents

Task

Total Sample Size

Estimated Response Rate

Number of Respondents

Responses

Time Estimate (in hours)

Number of Admini-strations

Total Hours

Hourly Rate

Estimated Monetary Cost of Burden

School Year 2007-2008

Teacher Survey –

Fall

252

85%

214 Teachers

214

0.5

1

107

$40

$4,280

Teacher Survey - Winter

252

85%

214 Teachers

214

0.25

1

54

$40

$2,160

Teacher Survey - Spring

252

85%

214 Teachers

214

0.5

1

107

$40

$4,280

Teacher Knowledge Inventory

252

85%

214 Teachers

428

0.75

2

321

$40

$12,840

Extant Data Collection Protocol

84

100%

84 School Administrators

168

1

2

168

$50

$8,400

Totals







757


$31,960

School Year 2008-2009

Teacher Survey –

Fall

252

85%

214 Teachers

214

0.5

1

107

$40

$4,280

Teacher Survey - Winter

252

85%

214 Teachers

214

0.25

1

54

$40

$2,160

Teacher Survey - Spring

252

85%

214 Teachers

214

0.5

1

107

$40

$4,280

Teacher Knowledge Inventory

252

85%

214 Teachers

214

0.75

1

161

$40

$6,440

Extant Data Collection Protocol

84

100%

84 School Administrators

252

1

3

252

$50

$12,600

Totals







681


$29,760

Annual Avg.





926



1492


$61,720




  1. Estimate of Cost Burden to Respondents

There are no additional respondent costs associated with this data collection other than the hour burden accounted for in item 12.

  1. Estimate of Annual Cost to the Federal Government

The estimated cost for all aspects of the study is $20,996,081 over five years, making the annual cost to the federal government $4,199,216.



  1. Program Changes or Adjustments

When OMB migrated version 1 of this collection into ROCIS, there were two differing NOA's generated by OMB. The electronic version of the NOA showed 51 burden hours. The Rocis generated NOA approved 1011 burden hours. Phase two of the collection is in clearance now and this problem has been discovered. Since the burden hours from the first phase (pilot and recruitment efforts) are completed and are no longer needed, the program office is deducting the 1011 hours (from the ROCIS NOA) from the burden hours being requested to come up with the amount of the program change. This program change is calculated as being an increase of 481 hours (1492 hours- 1101 hours=481 hours).



  1. Plans for Tabulation and Publication of Results

Data collection for the Mathematics PD Impact Study will begin in July, 2007 and will end in August, 2009. Findings will be reported to IES by AIR and MDRC in two substantive reports. The schedule for the dissemination of these reports is summarized in Exhibit 10.



Exhibit 10. Schedule for Dissemination of Study Results

Activity/Deliverable

Due Date

First Report

Summer 2009

Final Report

Summer 2010





The first report will focus on analyses of the data collected during the 2007-08 school year. This report will include a description of the study design (i.e., treatments, sample size, study sites) and employed methodology. The descriptive analyses will include the following:

  • Description of the school districts and schools in the treatment and control groups;


  • Description of the treatment and control groups which address group equivalence after randomization;


  • Descriptive information on the fidelity of implementation of the treatments and dosage of professional development delivered to the treatment group; and


  • Description of the rate of student and teacher mobility over the period following random assignment, and the characteristics of students and teachers entering and leaving the study schools.


The report will also provide results regarding the effects of the treatments on the three outcome measures during the treatment year: teacher knowledge, teacher practice, and student achievement between.

The final report will be a capstone report summarizing the entire project and its results. The main focus of the report will be the results pertaining to the effects of the treatments on the three outcomes during the year after the treatment (e.g., persistence or late appearance of effects, depending on the first-year results). In addition, the report will examine (1) the possible relationships between teacher experience or prior knowledge and the impact of the interventions, (2) the relationship between student characterstics and impact, (3) the relationship between dosage of professional development received and impact, and (4) the cost of the treatments. (See the Description of the Mathematics PD Impact Study for a more complete discussion of the research questions that will be addressed.) The report also will include a comprehensive analysis of teacher and student mobility and its potential effects on study results.

Both reports will require complex analytical techniques in order to estimate impacts. In both reports, we will compare schools that are randomly assigned to receive an intervention with those that are not. Because treatment groups are determined at the school level, the primary unit of analysis will be the school. The average outcome levels in the group of schools not receiving the intervention in question represents a reliable estimate of the achievement levels that would have been observed for the treatment group schools in the absence of the program. Therefore, the difference between the average outcomes in the schools that receive the particular intervention and those randomly assigned to “business as usual” in the district represents a reliable and unbiased estimate of the intervention’s impact.

The data for this evaluation can be thought of as hierarchical or nested. Students are nested within classrooms or teachers, and teachers and classrooms are nested within schools. Since units at the same level are not statistically independent from one another, the most appropriate way to estimate the effect of the intervention on student achievement and to correctly estimate the statistical precision of these estimates is to apply a multilevel model—estimating separate models at the student, classroom, and school levels.

Level 1: Students-within-Classrooms-within-Schools

Our system of equations begins at the student level. Equation 1 describes the relationship between student achievement, individual background characteristics, and random variation among the students in each classroom.

(1)

In this model,

= mathematics achievement of student i, in classroom j, at school k; and

= individual student characteristics (e.g., prior academic achievement, race/ethnicity, free and reduced price lunch status, etc.) of student i, in classroom j, at school k, centered on the grand mean across the sample).


Therefore,

= average achievement in classroom j, at school k, for students with average characteristics and prior achievement;


= the relationship between individual student characteristics and student achievement within classroom j at school k; and


= the difference between the achievement of student i and average achievement in classroom j at school k (adjusted for student background characteristics).


Level 2: Classrooms-within-Schools

(2)

. (3)

= average achievement at school k; 1

= difference between average achievement in classroom j at school k and average achievement at school k; and


= relationship between individual characteristics and student achievement at school k.


Level 3: Schools

Given that random assignment occurs at the school level, program impacts are estimated at this level of the system of equations.

(4)

, (5)

where

= 1 if school k is in district d, 0 otherwise;

= 1 if school k is in the treatment group, 0 otherwise;

= the average outcome for schools in district d.


= the difference between average achievement at schools randomly assigned to the treatment group versus schools assigned to the control condition in district d (i.e., the effect of the intervention on student achievement in district d).


= the difference between average achievement in school k and average achievement in district d


= the average pretest slope for students in schools in district d.



This multilevel system of equations can be estimated using Hierarchical Linear Modeling (HLM) software, or it can be solved into a composite equation and estimated using SAS Proc Mixed. The analytical strategy regarding teacher knowledge and teacher instruction outcomes is similar. The primary difference is that because there is no “within classroom” variation in teacher characteristics, and therefore the analytic model involves two levels (teachers nested within schools) rather than three. For the teacher practice outcome, we will lack a pre-treatment measure of teachers’ practice to use as a covariate to increase precision.



  1. Approval to Not Display OMB Expiration Date

Approval is not being requested; all data collection instruments will include the OMB expiration date.



  1. Explanation of Exceptions

No exceptions are requested.

References


Ball, D. L. (1996). Teacher learning and the mathematics reforms: What we think we know and what we need to learn. Phi Delta Kappan, 77, 500-08.


Ball, D., Rowan, B and Hill, H. (2003). Effects of teachers' mathematical knowledge for teaching on student achievement. Paper presentation at the annual meeting of the American Educational Research Association.


Bloom, H.S. (2003) Sample design for an evaluation of the Reading First Program. New York: MDRC.


Bos, C. S., Mather, N., Narr, R. E., & Babur, N. (1999). Interactive, collaborative professional development in early literacy instruction: Supporting the balancing act. Learning Disabilities Research and Practice, 14, 227-238.

Carpenter, T.P., Fennema, E., Peterson, P.L., Chiang, C., & Loef, M. (1989). Using knowledge of children’s mathematics thinking in classroom teaching: An experimental study. American Educational Research Journal, 26, 499-531.


Cohen, D.K. & Hill, H.C. (2001). Learning policy: When state education reform works. New Haven: Yale University Press.

Cohen, D. K., & Hill, H. C. (1998). Instructional policy and classroom performance: The mathematics reform in California (RR-39). Philadelphia: Consortium for Policy Research in Education.

Cohen, Jacob. 1988. Statistical Power Analysis for the Behavioral Sciences. Hillsdale, NJ: Lawrence Erlbaum.

Education Commission of the States (2003). Eight questions on teacher preparation: What does the research say? Denver, CO: Author.

Elmore, R. (2002). Bridging the gap between standards and achievement: The imperative for professional development in education. [Online.] Available: http://www.ashankerinst.org/Downloads/Bridging_Gap.pdf.


Garet, M, Porter, A, Desimone, L, Birman, B., & Yoon, K. (2001). What makes professional development effective? Results from a national sample of teachers. American Educational Research Journal, 38, 915–945.

Garet, M., Birman, B. F., Porter, A. C., Desimone, L., Herman, R., & Yoon, K. S. (1999). Designing effective professional development: Lessons from the Eisenhower program. Washington, DC: American Institutes for Research.

Gearhart, M., Saxe, G.B., Seltzer, M., Schlackman, J., Ching,C.C., Nasir, N., Fall, R., Bennett, T., Rhine, S., & Sloan, T.F. (1999). Opportunities to learn fractions in elementary mathematics classrooms. Journal for Research in Mathematics Education, 30, 286-315.


Grant, S. G., Peterson, P. L., & Shojgreen-Downer, A. (1996). Learning to teach mathematics in the context of systemic reform. American Educational Research Journal, 33, 502-541.


Hargreaves, A. and Fullan, M. G. (1992). Understanding teacher development. London: Cassell.


Hill, H., Schilling, S., & Ball, D. (2004). Developing measures of teachers' mathematics knowledge for teaching. Elementary School Journal, 105, 11-30.


Kennedy, M. (1998). Form and substance in inservice teacher education. Research Monograph No. 13. National Institute for Science Education. Madison, WI: University of Wisconsin.


Knapp, M. S. (1997). Between systemic reforms and the mathematics and science classroom: The dynamics of innovation, implementation, and professional learning. Review of Educational Research, 67, 227-266.


Lieberman, A. (1996). Practices that support teacher development: Transforming conceptions of professional learning. In M. W. McLaughlin & I. Oberman (Eds.), Teacher learning: New policies, new practices (pp. 185-201). New York: Teachers College Press.


Lieberman, A., & McLaughlin, M. W. (1992). Networks for educational change: Powerful and problematic. Phi Delta Kappan, 73, 673-677.


Lipsey, Mark, 1990. Design Sensitivity: Statistical Power for Experimental Research. Newbury Park, CA: Sage Publications, Inc.


Little, J. W. (1993). Teachers’ professional development in a climate of educational reform. Educational Evaluation and Policy Analysis, 15, 129-151.


Loucks-Horsley, S., Hewson, P. W., Love, N., & Stiles, K. E. (1998). Designing professional development for teachers of science and mathematics. Thousand Oaks, CA: Corwin Press, Inc.


McCutchen, D., Abbott, R. D., Green, L. B., Beretvas, S. N., Cox, S., Potter, N. S., Quiroga, T., & Gray, A. (2002). Beginning literacy: Links among teacher knowledge, teacher practice, and student learning. Journal of Learning Disabilities, 35, 69-86.

Milgram, J.R. (2004).The mathematics that pre-service teachers need to know. Department of Mathematics. Stanford, CA: Stanford University.



National Research Council. (2001). Adding it up: Helping children learn mathematics. J. Kilpatrick, J. Swafford, and B. Findell (Eds). Mathematics Learning Study Committee, Center for Education, Division of Behavioral and Social Sciences and Education. Washington, DC: National Academy Press.

O’Connor, R. E. (1999). Teachers learning Ladders to Literacy. Learning Disabilities Research and Practice, 14, 203-214.

Rowan, B., Correnti, R., & Miller, J. (2002). What large-scale survey research tells us about teacher effects on student achievement: Insights for the Prospects study of elementary schools (CPRE Research Report Series RR-051). Philadelphia: Consortium for Policy Research in Education.

Rowan, B. (2005). NCEE workshop on measuring classroom practice. Presented at the US Department on September 27, 2005.


Sanders, W. and Rivers, J. (1996). Cumulative and residual effects of teachers on future academic achievement. Knoxville, Tenn.: University of Tennessee Value-Added Research and Assessment Center.


Silver, E.A. & Kenny, P.A. (2000). Results from the seventh mathematics assessment of the National Assessment of Educational Progress. Reston, VA: National Council of Teachers of Mathematics.


Silver, E. A., & Stein, M. K. (1996). The QUASAR project: The "revolution of the possible" in mathematics instructional reform in urban middle schools. Urban Education, 30(4), 476-521.


Hiebert, James, Ronald Gallimore, Helen Garnier, Karen Bogard Givvin, Hilary Hollingsworth, Jennifer Jacobs, Angel Miu-Ying Chui, Diana Wearne,Margaret Smith, Nicole Kersting, Alfred Manaster, Ellen Tseng,Wallace Etterbeek, Carl Manaster, Patrick Gonzales, and James Stigler.(2003). Teaching Mathematics in Seven Countries: Results From the TIMSS 1999 Video Study, (NCES 2003–013 Revised). Washington, DC: U.S. Department of Education, National Center for Education Statistics.


Stiles, K., Loucks-Horsley, S., & Hewson, P. (1996). Principles of effective professional development for mathematics and science education: A synthesis of standards (NISE Brief, Vol. 1). Madison, WI: National Institutes for Science Education.


Talbert, J. E., & McLaughlin, M. W. (1993). Understanding teaching in context. In D. K. Cohen, M. W. McLaughlin, & J. E. Talbert (Eds.), Teaching for understanding: Challenges for policy and practice (pp. 167-206). San Francisco: Jossey-Bass, Inc.


Tirosh, D., Fischbein, E., Graeber, A.O., & Wilson, J.W. (1999) Prospective elementary teachers’ conceptions of rational numbers. Available: http://jwilson.coe.uga.edu/Texts.Folder/tirosh/Pros.El.Tchrs.html.


Whitehurst, G. J. (2002, Summer). Improving teacher quality. Spectrum: The Journal of State Government, 12-15.



1 We may include a small number of fixed teacher-level variables (for example, undergraduate mathematics major) as covariates in equation 2.


File Typeapplication/msword
File TitlePROFESSIONAL DEVELOPMENT IMPACT
AuthorSCronen
Last Modified ByDoED
File Modified2007-05-09
File Created2007-05-09
© 2024 OMB.report | Privacy Policy