Supporting Statement Part A
Supporting Statement Part A.doc
The Effects of Odyssey Math Software on the Mathematics Achievement of Selected Fourth Grade Students
OMB: 1850-0830
Effects of Odyssey® Math Software on the Mathematics Achievement of Selected Fourth Grade Students in the Mid-Atlantic Region: A Multi-Site Cluster Randomized Trial
Supporting Statement for Request for OMB Approval of Data Collection Instruments
Section A. Justification
Submitted: January 7, 2007 Revision Submitted: March 21, 2007
Kay Wijekumar, Ph.D. John Hitchcock, Ph.D.
|
TABLE OF CONTENTS
Page
INTRODUCTION 1
A.JUSTIFICATION 2
1. Circumstances That Make Data Collection Necessary…………………………........2
2. How, by Whom, and for What Purpose the Information Is To Be Used .3
3. Use of Information Technology .6
4. Efforts to Identify and Avoid Duplication .7
5. Impacts on Small Businesses and Other Small Entities .8
6. Consequences to Federal Programs or Policies if Data Collection is Not Conducted .8
7. Special Circumstances .9
8. Solicitation of Public Comments and Consultation with People Outside the Agency .9
9. Justification for Respondent Payments …………………………………………..... 9
10. Confidentiality Assurances 10
11. Additonal Justification for Sensitive Questions 11
12. Total Annual Hour and Cost Burden to Respondents 12
13. Estimates of Total Annual Cost Burden to Respondents or Record Keepers………14
14. Estimate of Total Cost to Government 15
15. Program Changes or Adjustments 15
16. Tabulation, Analysis and Publication of Results 15
17. Approval Not to Display the Expiration Date for OMB Approval 28
18. Exception to the Certification Statement 28
LIST OF EXHIBITS
Exhibit A ODYSSEY MATH® THEORY OF ACTION
Exhibit B INVITATION TO EXPRESS INTEREST IN STUDY
Exhibit C SUPERINTENDENT LETTER
Exhibit D MEMORANDA OF UNDERSTANDING
Exhibit E SCHOOL INFORMATION SHEET
Exhibit F TEACHER SURVEY
Exhibit G TEACHER INFORMED CONSENT FORM
Exhibit H PARENT WAIVER OF CONSENT FORM
Exhibit I STUDENT ASSENT FORM
Exhibit J FIDELITY OBSERVATION CHECKLIST
Exhibit K Odyssey Math Fact Sheet
Exhibit L SAMPLE LIST OF MAILING ADDRESSES
Exhibit M Sample demographic report to be generated by Schools for REL MA data analysis purpose
Exhibit N Odyssey MATH Intervention Professional Development Package Description
LIST OF APPENDICIES
Appendix A COMPUTER REQUIREMENTS FOR USE OF ODYSSEY MATH
Appendix B COMPASSLEARNING WEB-BASED RESOURCES AND PEER
SUPPORT
Appendix C INTERMEDIATE UNITS IN PENNSYLVANIA
Appendix D FLOW OF CLASSROOMS AND STUDENT FROM BASELINE
THROUGH REPORTING
INTRODUCTION
This document presents the Supporting Statement for a multi-site cluster randomized control trial (or multi-site CRT) designed to test the impacts of Odyssey Math Software in fourth grade classrooms in the Mid-Atlantic region of the United States (i.e., Pennsylvania, Maryland, New Jersey, Delaware and the District of Columbia), during the 2007-08 academic year.1 We are requesting OMB approval for the following data collection activities:
recruitment of schools and participating teachers
teacher informed consent
teacher background survey
sample memorandum of understanding
pre and post academic achievement testing
treatment fidelity and control group observation checklists
notification of parents
parental completion of a waiver of consent form (if they choose not to allow their child to participate in the study)
school information request sheets
Support for the idea of developing stronger mathematics curricula comes from national organizations such as the National Council of Teachers of Mathematics (NCTM), the US Department of Education, and the American Federation of Teachers (AFT). Leaders in each organization call for their members to change their instructional practices to meet the NCTM Standards, which emphasize instruction in mathematical “habits of mind,” rather than memorization, to solve mathematics problems (NCTM, 1989; NCTM, 1998). Despite the importance of mathematics education in K-12 schools, there have been a limited number of interventions that have the breadth, depth, and instructional strategies to deliver math instruction to students using computer technologies.
Odyssey® Math may be an exception. The intervention is a computer-based mathematics curriculum designed to offer opportunities to engage in more challenging mathematics in (presumably) interesting contexts. The developer, CompassLearning, designed the curriculum on the premise that for students to achieve at the highest levels in mathematics, they must first understand basic concepts. From there they can build new knowledge and understanding through what the developer describes as rich and rigorous content. The intervention is designed from a learning theorist’s perspective that not all students build new knowledge and understanding at the same time, and in the same way. Thus, the overarching approach of CompassLearning’s Odyssey® Math program is to assist students, from kindergarten through high school, learn fundamental skills and develop processes for inquiry and exploration, as well as to provide a meaningful context for applying ideas, and tools.
Despite the promise the intervention holds, existing studies on Odyssey® Math have not adequately controlled for threats to the internal validity. So in keeping with the No Child Left Behind Act of 2001 (P.L. No. 107-110), which requires that education decision makers base instructional practices and programs on scientifically valid research, the Regional Education Lab-Mid-Atlantic has designed a multi-site CRT to evaluate the effectiveness of Odyssey® Math in improving math scores. The evaluation will use an experimental design where classrooms will be randomly assigned, within schools, to Odyssey® Math or control (i.e., business as usual) conditions. The experimental condition will use Odyssey® Math Software for 60 minutes each week and control classrooms (again, in the same schools) will use their standard mathematics curriculum.
This submission provides an overview of all aspects of the planned data collection, subsequent analyses, and reporting. It also provides details on forms used for teacher informed consent, a teacher background survey, parental waiver of consent, student assent, measures used for data collection, and observation checklists. In addition, the submission includes estimates of respondent burden associated with the data collection efforts.
A. JUSTIFICATION
Circumstances That Make Data Collection Necessary
The Regional Education Laboratory, Mid-Atlantic (hereafter referred to as the Lab) is planning a multi-site CRT to study the effects of Odyssey® Math Software on the mathematics achievement of fourth grade students in the Mid-Atlantic region. Mathematics education is becoming increasingly important in a global society; meanwhile, there is a dearth of scientifically valid evidence to support the use of one instructional approach over another. The systematic review the What Works Clearinghouse (WWC) conducted on Mathematics instruction has found only a few studies that used internally valid research designs.
The review of Odyssey® Math identified five empirical studies and none met WWC evidence screens because the researchers did not use a strong causal design that creates comparable groups. Another review, "Technology Solutions that Work," identified similar methodological shortcomings in studies on Odyssey® Math. Factors other than Odyssey® Math were not controlled for when researchers estimated the impact of the curriculum on student achievement. In other words, the effect size estimates from this research were probably biased.
A study by Learning Point Associates charted the progress of three schools that used the CompassLearning fourth grade level curriculum as part of their school reform program. To assess the impact on mathematics achievement, researchers compared the performance of students in the intervention year with students in the previous year on the state's NCLB test (MCAS). They reported the increases in the percentages of students scoring at the "Proficient" rating or above in each of the three schools at 23.7%, 32.3%, and 22.6% compared to a statewide increase of only 8%. Effect sizes were presented, but they were calculated inappropriately, so they are not reported here.2 More importantly, in the absence of a valid group of control schools, it is impossible to determine causality — whether the percentage increases were caused by Odyssey® Math or some other factor(s).
Other studies in the WWC review present similar correlational evidence with some studies suggesting the product improves student math achievement and other studies suggesting the product has no effect. Given the correlational nature of the existing research on Odyssey® Math, and their equivocal findings, the primary lesson learned from the WWC review is that there is a need for a randomized controlled trial that is sufficiently powered, well designed (e.g., creates comparable groups at baseline and maintains this comparability to the end of the trial), and is implemented with high fidelity (i.e., the methodological characteristics of the study adhere to well-established standards for a randomized controlled trial). A trial of this kind would generate unbiased estimates of the effects of CompassLearning on outcomes of interests such as student achievement. Filling this void in the education research literature, and more importantly, in the education curriculum policy arena is pertinent.
Though there is a lack of valid empirical evidence to justify the financial investment in the Odyssey® Math product for classrooms, the developer claims that thousands of elementary schools in the U.S. invest large amounts of time, money and other instructional resources to use Odyssey® Math. This may be due, in part, to how the intervention was designed. Consistent with the company’s overall approach to instruction, CompassLearning developed certain components of the curriculum that differentiate and target mathematics instruction according to student needs. The combination of direct instruction, guided feedback, and exploration purportedly allows students to develop an in-depth understanding of mathematics. According to the developer, Odyssey® Math features the best practices for mathematics concept development and instruction by blending skill-building with a problem-based approach that allows students to expand their knowledge and gradually increase their problem-solving skills.
Given that the intervention is widely used but supported by a research base that consists solely of quasi-experiments with potentially biased estimates of the intervention’s effectiveness, the data collection activities for the proposed RCT is warranted. The Lab proposes data collection activities designed to minimize the burden on teachers and students and to generate evidence to rigorously address the following research questions:
Do Odyssey® Math fourth grade classrooms outperform control classrooms on the mathematics subtest of the TerraNova CTBS Basic Battery?
What is the effect of Odyssey® Math on the math performance of males and female students?
What is the effect of Odyssey® Math on the math performance of low and medium/high achieving students?3
The presumed causal influences in the study are outlined in the theory of action (Exhibit A). The study assumes that the intervention influences teacher and student behavior through professional development activities and the introduction of the software (used as a supplement to existing curricula during the regular school day). Provided the intervention is used with fidelity, it is assumed that Odyssey® Math will impact teacher knowledge and practice while simultaneously influencing student motivation and the use of graduated learning strategies. These in turn will influence student achievement, which is the focus of the proposed impact study. Student achievement will be assessed using the TerraNova. The study will be conducted in schools that commit fourth grade teachers and all their classrooms to random assignment, are not already using the intervention, and have the technology platforms needed to use the software. As noted above, the Lab plans to conduct analyses on whether Odyssey® Math has differential outcomes for males and females, as well as high and low achievers, as there is extensive empirical literature on the factors and mathematics achievement
To be eligible to participate in the study, teachers must meet three requirements: (a) can teach math, (b) are willing to use the intervention and (c) are not already using Odyssey® Math. The general schedule for the proposed study will be to have teachers complete background surveys and randomly assign classrooms to conditions during the summer of 2007. The intervention will follow the completion of the student assent forms in September 2007. Student baseline performance in math will be assessed via the Terra Nova Basic Battery (Form A). This will be followed by three fidelity observations conducted by Lab personnel at the beginning, middle, and end of the 2007-2008 academic year. We also document teaching in the control conditions via checklists to provide contexts for observed program impacts. In spring 2008, students will complete the Terra Nova Basic Battery Form A post-test.4 We assume most participating schools will have four classrooms available for random assignment resulting in two classrooms per condition (Odyssey® Math and control). As our power analyses will show later in this submission, we will need 31 schools to participate in the study. We assume this will yield approximately 124 classrooms and 2480 students.
In conclusion there is an immediate and important need to conduct a careful research study on the effectiveness of the Odyssey Math software in elementary schools. There have been extensive calls for improving mathematics learning experiences for students. In response to these calls, CompassLearning, Inc., created Odyssey® Math to address many of the identified challenges. The software has gained in popularity and the developer claims it is now used in over 2000 schools. Nevertheless, there have been no studies that unequivocally found a causal link between use of Odyssey® Math software and improved learning in mathematics. Reviews of research on Odyssey® Math by "Technology Solutions that Work" and the What Works Clearinghouse (WWC) have identified serious methodological shortcomings in studies that comprise the current empirical research base on CompassLearning. Specifically, these studies did not use a strong causal design with the internal validity, such as a comparable control group formed through random assignment, necessary to casually attribute student gains in math achievement to Odyssey® Math.
How, by Whom, and for What Purpose the Information Is To Be Used?
Study Approach (how the information is collected)
The authors of this study propose using a multi-site cluster randomized trial (or multi-site CRT). In what follows, we describe all associated burden to the students, teachers, and schools, as well as proposed statistical analyses and reporting schedules.
Description of Data Collection
Data collection efforts and analyses will be led by Co-PIs with support from Analytica and a statistical analysis expert from The Pennsylvania State University.
The data collection plan for this research starts with the agreement to participate with the schools and is followed by teacher demographics surveys, professional development, notifying parents of the waiver of consent, student pre-tests, one full year of data collection, and a post-test. The respondents, mode of data collection, timeline, and key data to be collected at each stage are presented in Table 1. Details about each instrument follow the table.
TABLE 1
DATA COLLECTION PLAN5
Respondent |
Mode |
Timeline |
Key Data |
Teachers |
Teacher informed consent |
June 2007 |
Teacher agreement to participate in the research. |
Teachers |
Teacher Demographics Survey on-line6 |
June-July 2007 |
Demographic information and math teaching and technology experience. |
Schools |
Agreement to Participate in Study |
Summer 2007 |
Letter stating that the school will implement Odyssey Math for at least 60 minutes each week during the academic year. |
Schools |
School/classroom data information request sheet |
Summer 2007 |
Most of the time, needed data can be collected via the Internet. For example, the Pennsylvania Dept of Education tracks computer lab availability and the percentage of economically disadvantaged and minority students in their on-line data sources at the school level. However, schools will be asked to complete information specific to the fourth grade classrooms. |
Parents |
Waiver of Consent Form (IF they choose NOT to participate) |
August September 2007 |
Agreement to participate. |
Students |
Informed Assent Form |
September 2007 |
Agreement to participate in the study. |
Students |
Pre-test |
September 2007 |
Pre-test math assessment. |
Teachers |
Fidelity Observations of Teachers |
September 2007 through April 2008 (3 times through the year) |
Descriptive information to support the statistical analysis of data in the study. Description of instructional objectives, strategies, and use of technology. |
Students |
Post-test |
April – May 2008 |
Post-test math assessment to assess the improvement through the year. |
Teacher Informed Consent
Teachers participating in the study will be given an outline of the project and be notified whether they will be in the experimental or control group. The teachers will be also notified that there will be three observations during the academic year to collect information on treatment and control implementation and provide descriptive data for the statistical analyses. The consent form is in Exhibit G.
Parent Waiver of Consent Form
The parents of students in fourth grade of participating schools will be sent a letter with a waiver of consent form that they will return if and only if their child is not allowed to participate in the study. This method will be used pending approval from each School District (local IRB or school legal counsel) and The Pennsylvania State University IRB. Generally speaking, waiver of consent can be used with USDOE studies that use academic interventions and outcomes. The consent form is in Exhibit H.
Student Assent Form
The students who have their parents’ permission to participate will be given a description of the project by the teacher. At that time the teachers will ask the students if they are willing to participate in the project. They will also be advised that they can withdraw their participation at any time during the project. The consent form is in Exhibit I).
Teacher Demographics Survey on-line for intervention and control teachers
The teachers will be completing this survey designed to gather information about their degrees, years of teaching, and experience with technologies. The survey will be included as part of the 2 day Odyssey Math training planned during the summer and will take approximately 10 minutes to complete in a web-based interface designed to minimize the burden of completing a paper form. However, the control group teachers cannot attend the summer training during that time and therefore they will be given a paper version of the same form with a self-addressed stamped envelope to return the survey to the Lab. The survey is in Exhibit F.
Student Pre-Test
TerraNova Math Subtest. TerraNova CTBS Basic Battery (Basic Battery), published by CTB/McGraw-Hill, will be used as the only outcome measure of this study. The Basic Battery edition consists of the Reading/Language Arts subtest and the Mathematics subtest, which can and will be administered separately. For the Mathematics subtest, content objectives reflect the National Council of Teachers of Mathematics (NCTM) Standards as well as state and local curriculum documents and the conceptual framework of NAEP.7 This fourth grade math subtest is comprised of 57 selected-response items and takes 1 hour and 10 minutes to administer. Form A of the Basic Battery will be administered as the pre- and post-test measures of math achievement of this study, and in accordance with the test developer’s recommendation.8 For the math sub-test, internal consistency measured with the Kuder-Richardson formula 20 (KR20) coefficient is .93 and standard error of measurement (SEM) is 3.13.
TerraNova Forms. The Terra Nova CTBS has three forms (A, B, and C). Form A was initially normed in 1997 followed by an update in 2005. Form B is a computerized version that cannot be used in this CRT. Form C (sometimes referred to as the second edition) was normed in 2003 but is unavailable for us to use with this CRT. It is embargoed in some parts of Pennsylvania and a number of other states, because the Battery is used as part of the State or District standardized assessment program. The same form A can be administered at pre and post-tests as suggested by the test developer.
Accommodations and Scoring. According to the publisher, a series of test accommodations are designed to further assist test users with administration and explain the potential implications for these accommodations on test result interpretation. Updated norms are representative of the K-12 student population and include students with disabilities and ELLs. In this study, 2005 norms will be used to interpret the test scores.9 To score the fourth grade math subtest, we will use the CTB/McGraw-Hill scoring service (which considers test accommodations), to minimize burden on teachers and to ensure accuracy of scores. Complete test score data files will be in ASCII format; and will also include selected student demographic information such as gender or student ID numbers as specified by the research team.
Administration. Where possible, the pre- and post-tests will be administered in the same common noise free setting (such as an auditorium) which will reduce the number of study personnel needed per school. We will, of course, negotiate with schools to work out the details of test administration on a school-by-school basis. The tests will be administered by the LESs or field research coordinators, or both (depending on the number of supervisors required), in collaboration with teachers during approximately the third week of the school year for the pretest and five weeks prior to the end of the school year (approximately the last week in April) for the post-test. The LESs and field research coordinators will be trained on the administration of the test and the teachers will be given written guidelines on the test administration.
Classroom Observations Checklist (to be used three times during the academic year)
A classroom observation checklist will include three subsections to document descriptive information about the math domain knowledge and strategies covered in the observed class period. Additionally, the checklist will include how the Odyssey® Math software was used in the classroom, and overall technology implementation. There will be two versions of this form created. The first will be for the experimental classrooms with questions specific to Odyssey® Math use. The second version will be for the control classrooms to document any use of other technologies. The observation forms are in Exhibit J.
Student Post-Test
Similar to the pre-test the post-test will use the TerraNova Basic Battery Form A.10
Use of Information Technology
Whenever possible, we will use information technologies to maximize efficiency when gathering data and to minimize the burden on respondents. Initial recruitment will begin with electronic searches of existing data sources (e.g., Common Core Data) to identify eligible schools. Study staff will use electronic communication and telephone calls, in addition to mail, to gain district approval for school recruitment. Additionally, requests for student data will be managed by telephone and email so that school or district staff can provide us with student data in electronic form.
The intervention teachers will complete their demographics survey on the WWW during the summer 2-day training session. However, the control group teachers will be mailed the survey in hard copy format since they will not receive technology related training or instructions until the second year of the project (when they will have access to the Odyssey Math software as an incentive). They will be provided a self-addressed return envelope to send the survey back to the Lab.
TerraNova achievement measures will be scored using McGraw Hill’s (the TerraNova vendor) scoring service. The service will provide individual student data files, marked by a student ID, to the study team. The scoring service not only has the advantage of properly accounting for accommodations based on special needs and English language learner status, data files can also be readily uploaded to statistical software for analyses.
Computer log files from Odyssey Math will be used to calculate the time each student spent on the use of the software each week and to assess the quality of their work. This information will be used to supplement observations of intervention fidelity and thereby reduce the study teams need to be present in classrooms.
Efforts to Identify and Avoid Duplication
Judging from results the What Works Clearinghouse has published to date, the proposed multi-site CRT of Odyssey® Math is, at the time of this writing, the only study designed to use a rigorous design to test the impacts of the software. The data to be collected is necessary to provide reasonable descriptions of the sample and sites, as well as to estimate the impact of Odyssey® Math relative to a counterfactual (i.e., group of control classrooms). The Mid-Atlantic Regional Educational Lab has created a checklist that captures the necessary data on fidelity observations as well as the teacher survey. These forms were generated by synthesizing many sources of information and creating the minimal amount of questions that can still help provide descriptive information necessary to assess the impact of the Odyssey® Math software.
Observation Checklists. Classroom observations will be conducted using two different checklists. One checklist was developed to assess if critical elements of Odyssey® Math are used in the treatment condition, and to document overall implementation fidelity. A second checklist developed by Stonewater (1996), will be used to document mathematics instruction in control and treatment classrooms during times when Odyssey® Math is not being used (the checklist was updated by consultants with expertise in mathematics instruction and content, as the original form is based on previous NCTM standards). These checklists will use simple Likert-type response formats and study personnel will be instructed to use them without interacting with the classroom and interrupting instruction. These checklists are needed to describe treatment and control instruction and serve as a check for the unlikely event that there is cross teacher contamination, where control teachers somehow gain access to and use the software. This is unlikely given the software is password protected and proper use requires extensive professional development. Nevertheless, findings will be more convincing if this is considered during classroom observations.
Teacher Background Survey. The following teacher characteristics will be compared across conditions: years of teaching experience, level of education, number of hours of professional development in mathematics instruction (during the past year), and number of hours of professional development in using computer-technology to teach (during the past year). The teacher background survey is needed to describe the degree of professional development associated with mathematics instruction and computer use educators have in the treatment and control classrooms, as school records will likely not have accurate and current information about these characteristics.
Classroom & Student Characteristics. The analyses will also consider mean pre-test at the classroom level, proportion of ethnicity/minority, proportion of free or reduced-price lunch status, proportion of special needs students, and proportion of English language learners. These data should be readily available from school records. We will also include gender and student achievement status at pre-test in separate HLM models. Student-level data for these characteristics can be questionable or difficult to tie to specific answer sheets. McGraw-Hill will therefore create response sheets that will capture gender and we will rely on pretest scores to identify low achieving students (i.e., students who score at or below the third grade).
Achievement Measures. Student mathematics achievement data cannot be obtained from state assessments because these are administered only once during the year, whereas we require assessment data at baseline (of course, at post-test as well) to obtain better precision of the impact estimates and help assess whether randomization was successful. Furthermore, all students in the study must take the same assessment and we plan to recruit from multiple states that do not use the same tests. Indeed, these will likely vary greatly in purpose, content and psychometric properties such as how they were normed. On a related matter, state achievement data may not be provided on a timely basis. Other research organizations (e.g., Mathematica Policy research) have reported on having to wait up to six months to receive state data and this would seriously delay completion of the project.
Impacts on Small Businesses and Other Small Entities
Schools are considered small entities and the research plans are designed to minimize their burden using four approaches. First, the Lab will use existing information from Federal and State databases on school demographics minimizing the data that schools have to provide. Second, the Lab will support the mailing of letters and information to parents by using Lab resources. Third, the administration of all assessments will be managed by Field Research Coordinators trained by the Lab to minimize the burden on the school. Finally, classroom observations of the teachers will be conducted using trained Field Research Coordinators who will be non-intrusive to the classroom environment and conduct the observations during only three class periods during the school year.
Consequences to Federal Programs or Policies if Data Collection is Not Conducted
NCLB requires states to improve mathematics achievement, but as noted above, few curricula have been investigated using rigorous trials. However, Odyssey® Math is a widely available intervention that is at least supported by quasi-experimental research of varying quality. This makes it a promising intervention, but failure to conduct the study will leave open an existing knowledge gap about mathematics instruction. The data collection for which we are requesting clearance: (a) Terra Nova baseline and outcome measures, (b) observation checklists, (c) teacher background surveys and (d) school/classroom descriptive data are critical for assessing intervention impacts and understanding the context in which the intervention is carried out.
Special Circumstances
No special circumstances apply to this study.
Solicitation of Public Comments and Consultation with People Outside the Agency
a. Federal Register Announcement
IES will prepare the Federal Register Notice.
b. Consultations Outside the Agency
The research team has consulted with a number of people with expertise in randomized controlled trials, multi-level analyses, and mathematics instruction. These experts include members of our Technical Working Group (experts gathered to guide rigorous design studies, as stipulated in all IES lab contracts), consultants at Mathematica Policy Research, and general advisors.
TABLE 2
LIST OF CONSULTANTS
Consultants |
||
Expert |
Affiliation |
Telephone Number |
Dr. Robert Boruch |
University of Pennsylvania |
(215) 898-0409 |
Dr. Rebecca Maynard |
University of Pennsylvania |
(215) 898-3558 |
Dr. Pui-Wa Lei* |
Pennsylvania State University |
(814) 865-4368 |
Dr. Herbert Turner |
Analytica |
(215) 808-8880 |
Dr. Michael Puma |
President of Chesapeake Research Associates, LLC |
(410) 897-4968 |
Dr. John Deke |
Mathematica Policy Research |
(609) 799-3535 |
Dr. Ed Smith |
Pennsylvania State University |
(814) 865-1201 |
*Also a study team member
Justification for Respondent Payments
The Lab is limiting incentives so that we can control any effects that the incentives may have on the outcomes of the study. By limiting the incentives we are able to study the efficacy of the Odyssey® Math software as it would be used if the school opted to purchase and install the software.
The planned multi-site CRT has built in the incentives designed to recruit participating schools in a competitive environment where resources are scarce and schools are reluctant to participate in a trial where their students may be assigned to the control group. The following incentives were carefully chosen to address the recruitment challenges but minimize any potential impact on the outcomes of the research: The first incentive for participation is free use of the Odyssey® Math software by the intervention teachers and classrooms during Year 1 when the study is first implemented; students who were in the control group during Year 1 will be given free access to the software in the second year.
Teachers will have the opportunity to participate in professional development that comes with Odyssey® Math. The teachers will be paid for their time for attending the summer training sessions and school districts will be reimbursed the cost of substitutes during the academic year.
We have budgeted costs for training the school district’s curriculum coordinators in use of the Odyssey® Math software use to support a longer term implementation, if they choose.
The Lab will include a monetary incentive of $150.00 a day for 2 days of summer professional development and to complete the 10-minute teacher survey ($25.00), three classroom observations ($ 25 per each observation for 3 observations=$75.00). The school will be reimbursed for teacher aides during the school year if the teacher needs to attend any additional training. Again, this value pertains to control teachers since we will provide them with training after the trial is over. Each group will be pre-paid for each segment of their participation in the research project.
Students will be provided a snack after completing the pre and post-tests.
Confidentiality Assurances
The Mid-Atlantic Regional Educational Lab has worked with the Institutional Review Board at The Pennsylvania State University to seek and receive approval on the study and all its controls. The forms shown in Exhibits G-I show the teacher informed consent, parent waiver of consent, and child assent. The information on confidentiality assurance is central to the IRB process at Penn State and will be conducted in full compliance with ED regulations. Data collection activities will also be conducted in compliance with The Privacy Act of 1974, P. L. 93-579, 5 USC 552 a; the “Buckley Amendment, “ Family Educational and Privacy Act of 1974, 20 USC 1232 g; The Freedom of Information Act, 5 USC 522; and related regulations, including but not limited to: 41 CFR Part 1-1 and 45 CFR Part 5b and, as appropriate, the Federal common rule or ED’s final regulations on the protection of human research participants. Additionally, the following summary is compiled based on the PSU IRB application:
All students will use usernames and passwords and they will be identified by an assigned ID number. Only the co-PIs, the study manager, and Dr. Peck (Director of the Lab) will have access to the information linking the students with their ID number. Pre- and post-test data will be stripped of names once ID numbers have been affixed, and at no time will the results for individuals, teachers, classes, schools, or districts be reported.
The only data that will be reported will be aggregated. These data will describe the treatment and control conditions, as well as the pre-test performance of students classified as “high,” “average,” and “low.” Requests for any other information will be denied, except where required by law to release it.
All data and forms collected from the students will be stored in a secured file cabinet at the Penn State Beaver Campus, at the co-PI’s office.
All identifying information will be replaced with the ID numbers when scores and demographic data is entered into the statistical analys programs and HLM files for data analysis.
Responses to this data collection will be used only for statistical purposes. The reports prepared for this study will summarize findings across the sample and will not associate responses with a specific district or individual. We will not provide information that identifies individuals, schools, or districts to anyone outside the study team, except as required by law.
All copies of the informed consent forms will be maintained in the co-PI’s Penn State office in a locked cabinet with a signed copy returned to the participating teachers.
Similarly, any waiver of consent form returned will be carefully noted to remove the student’s information from the study and data analysis. This will be conducted by the Penn State co-PI and the forms will be maintained in the locked cabinet.
Access to sample selection data is limited to those who have direct responsibility for selecting the sample. At the conclusion of the research, these data will be destroyed.
Identifying information on schools, students, and parents is maintained on separate forms which are linked to the interviews only by a sample identification number. These forms are separated from the interviews as soon as possible.
Access to the hard copy documents collected from respondents is strictly limited. Documents are stored in locked files and cabinets. Discarded material is shredded.
Computer data files are protected with passwords and access is limited to specific users. With especially sensitive data, the data are maintained on removable storage devices that are kept physically secure when not in use.
Responses to this data collection will be used only for statistical purposes. The reports prepared for this study will summarize findings across the sample and will not associate responses with a specific district or individual. We will not provide information that identifies an individual or individual district to anyone outside the study team, except as required by law.
Additional Justification for Sensitive Questions
There will be no sensitive questions in the teacher survey instrument designed to collect demographic information, years of teaching experience, and technology experience. There will be no information collected from any other participants except the standardized TerraNova Basic Battery Form A test.
Total Annual Hour and Cost Burden to Respondents
Table 3 presents our estimate of each respondent’s burden and Table 4 presents the summary. The data collection summarized for the study in Table 3 includes schools’ letters of agreement to participate, teacher informed consent form, parent waiver of consent form, and student assent. Where needed, we will also use school information request forms if we cannot get adequate descriptive data on-line. Students will also complete a pre-test and post-test of the TerraNova Basic Battery Form A test. During the data collection, the Field Research Coordinators from the Mid-Atlantic Regional Educational Lab will conduct three classroom observations at the beginning, middle, and end of the school year to provide descriptive information for the statistical analysis procedures to be run on the quantitative data. In addition, we will collect baseline administrative records for all students in the sample using data that is readily available at the State Departments of Education, in each state where the study is planned. If any additional information is necessary the school or district staff will assist the team.
TABLE 3
BURDEN ESTIMATE FOR EACH STAGE OF THE RESEARCH DESIGN
Assumptions: 2,480 students in 124 classrooms (124 teachers), 8 Field Research Assistants (5 to 6 schools for each FRA) |
|||||
Instrument or Data Source |
Average Number of Respondents |
Number of Responses Per Respondent |
Number of Total Responses |
Average Time Per Response |
Total Burden (Hours) |
Parental waiver of consent form (Exhibit H) |
2,480 |
1 |
2,480 |
10 minutes |
413.33 |
Burden associated with mailing of consent forms by schoolsa/ (Exhibit L) |
31 |
1 |
31 |
60 minutes |
31.00 |
Burden associated with any additional information need on students b/ (Exhibit M) |
31 |
1 |
31 |
30 minutes |
15.55 |
Teacher consent (Exhibit G) |
124 |
1 |
124 |
5 minutes |
10.33 |
Teacher demographic surveys during summer training (Exhibit F) |
124 |
1 |
124 |
10 minutes |
20.67 |
Teacher meetings about observations with field research assistants (Exhibit J) |
124 |
3 |
372 |
25 minutes (Usually 1 class period ~50 minutes) three times during the academic year |
155.00 |
Teacher training (Odyssey Math 2 days in summer; 4 additional days throughout the school year) (Exhibit N) |
124 |
1 |
124 |
48 hours |
5,952.00 |
Total |
3,038 |
9 |
3,286 |
|
6,597.88 |
a/ REL-MA will generate all letters and forms (Exhibit H and I) and pay for mailing. The estimated burden is for schools to generate a mailing list for 4th graders to send parent consent waiver form and student assent form.
b/ School may be asked to generate demographic data on students for data analysis purposes.
Our assumptions for the study participants include 31 schools, 124 teachers, and 2,480 students. Summaries are provided in Table 4 below; these summaries were calculated from information in Table 3, which presents additional details about respondent burden such as individual items that contribute to the total estimated burden of time. The assessment burden has not been included in the burden hour total since assessments are exempt under the Paperwork Reduction Act. This assessment tests the aptitudes of students. In all, total respondent hours are 6,598. These hours include 413 hours estimated for the parents’ waiver of consent forms. However, it must be noted that the forms need to be completed and returned ONLY in the instance where the parent does NOT allow their child to participate in the study. Therefore this estimate is actually much higher than our expectations of approximately 1% of participants actually completing the forms.
There are minimal costs associated with each respondent as calculated in Table 4. For the time required to complete short surveys and informed consent forms we have estimated costs of $9420.98. There will be no capital equipment, start-up, or record maintenance requirements on the respondents. All of those burdens will be assumed by the Lab.
The teacher training and teacher administration of tests are not included in the respondent burden estimates earlier. The teachers will be paid in the summer to attend the training session. Teachers will assist Lab personnel in the administration of tests.
TABLE 4
RESPONDENT BURDEN COST ESTIMATES
Informant |
Number of Responses |
Number of Rounds |
Average Time Per Response (Hours) |
Total Respondent Time (Hours) |
Estimated Hourly Wage (Dollars) |
Estimated Lost Burden to Respondents (Dollars) |
Parents |
2,480a\ |
1 |
1/6 (10 minutes) |
413.0 |
14.95d\ |
6,174.35 |
Teachers (Consent & Survey) |
124b\ |
1 |
1/4 (15 minutes) |
31.0 |
14.95 |
463.45 |
Teachers (Observation related meetings) |
124 |
3 |
1.25 (25 minutes * 3) |
155.0 |
14.95 |
2,317.25 |
School District Staff (Mailing Consent Forms & School Survey) |
31c\ |
1 |
1.5 per school |
46.5 |
10.02e\ |
465.93 |
a\ Each parent of our target of 2,480 sample participants from 31 schools and 124 classrooms (with approximately 20 students per classroom) will receive a letter from the school. However, we expect that MOST parents will NOT return the form that withdraws participation of the child from the study. Therefore we present an overestimate of this cost.
b\ Teachers will complete an informed consent form, a demographics survey during the summer training, and be observed for 25 minutes three times during the data collection. The time spent in training is compensated separately and not included here. The time that the teachers may assist the field research coordinators in administering the pre- and post-tests is also not included in this total.
c\ The school districts (31 schools) may provide very limited information and therefore this is another overestimate. The majority of the information will be obtained from existing data files submitted by schools to the State Departments of Education in each participating state. We have made a high end estimate of 103 hours for administrative work on the project such as mailing letters to parents.
d\ 2003 Statistical Abstract of the U.S. Table No. 636: Average Hourly Earnings by Private Industry Group: 1980-2002 (estimate in table is for 2002).
e\ 2003 Statistical Abstract of the U.S. Table No. 251: Average Salary and Wages Paid in Public School Systems: 1980-2002 (estimate in table is for 2002).
Estimates of Total Annual Cost Burden to Respondents or Record Keepers
No start-up costs will be incurred on the respondents. All of those burdens will be assumed by the Lab.
Estimate of Total Costs to the Government
For the data collection activities for which OMB approval is currently being requested, the overall cost to the government for 2 years is $3,695,233.72. This includes
Thus, the overall costs to the government of the full range of the cluster randomized control trial over the entire two years of study period will be $3,695,233.72. This estimate is based on the evaluation contractor's previous experience managing other research and data collection activities of this type, and the amount that has been budgeted for the study. |
Program Changes or Adjustments
This is a new data collection effort.
Tabulation, Analysis and Publication of Results
Overview of Analysis Plan
This multi-site CRT is designed to detect the impact of Odyssey® Math against a counterfactual. The design entails randomly assigning fourth grade teachers, and all their class sections, to intervention and control conditions within each participating school (to clarify, teachers’ classrooms will be randomly assigned to either a treatment or control condition, but not both). Recall that Odyssey® Math is a computerized, supplementary curriculum (it can be used as its own curriculum but it will not be used that way in this study) that requires passwords to gain access, extensive teacher training for proper use, and continual on-line support. Given the nature of the intervention, control group contamination within schools (where control teachers are instructing students at the same grade level and on the same subject as intervention teachers) is expected to be negligible. It is unlikely that casual conversation between treatment and control teachers, or even sporadically exposing the control teachers to the program, will degrade the treatment impact. In short, Odyssey® Math is an excellent candidate for the multi-site CRT design.
The analyses plan that follows will address three research questions that are reiterated here for the readers’ convenience:
Do Odyssey® Math classrooms outperform control classrooms on the mathematics subtest of the Terra Nova CTBS Basic Battery?
What is the effect of Odyssey® Math on the math performance of males and female students?
What is the effect of Odyssey® Math on the math performance of low and medium/high achieving students?
Given the multi-level structure of the data, in which students are nested within classrooms, we address the research questions in this study using multi-level modeling (Raudenbush & Bryk, 2002). Three HLM models (presented in detail later on in this section) will be used, one for each question.11 The first model will estimate the impact of Odyssey® Math on student achievement, and is designed to address the first research question. To address the second question, the first model will be replicated with a gender interaction term to assess if there is a differential impact for boys and girls. The first model will be replicated again, but this time with a (dichotomous) prior achievement interaction term. That is, this third HLM analysis will include two subgroups based on initial achievement status. Students scoring at or below the third grade level at pre-test will be designated as low achievers; students scoring above the third grade level at pre-test will be designated as high achievers. Note that only simple impact analyses will be conducted in this study, so each interaction (i.e., gender and achievement) will be examined separately.
Where possible, we will use random (as opposed to fixed) effects analyses. Sniders & Bosker (1999) note that, in a three-level model, the use of 10 or more groups/sites is probably too large to be thought of as unique entities. In these cases, they recommend the use of random effects models.
Descriptive analyses will be used to examine the: (a) sample characteristics and baseline equivalence of the two study groups, (b) participant flow, and (c) level of implementation fidelity among the Odyssey classrooms. To conduct an intent-to-treat analysis, every attempt will be made to collect student data for students who withdraw from the study. Observation checklists will be used to document the fidelity of treatment implementation and the nature of mathematics instruction in control classrooms. Finally, effect sizes will be calculated to estimate the magnitude of program impacts, as will confidence intervals to determine whether the results are due to chance.
Sample Characteristics and Baseline Group Equivalence
Descriptive Analyses. Descriptive analyses will track the flow of participants and clusters during the pre-analysis stages of the trial (see Boruch, 1997; Flay et al., 2005). We will report the number of clusters and participants for each group (intervention and control) through the following stages of the trial:
Assessment of eligibility
Random Assignment
Follow-up
Analysis
The results will be reported as a flow chart adapted from the CONSORT and attached as Appendix D. We will also describe sample characteristics. This will entail examining the demographic composition of both the full sample and each of the study groups. If district- and state-level data are available, we will also compare the demographic characteristics of the participating schools with those of the districts or states where the schools are located, which will allow us to understand the extent to which the study sample is similar to the larger population. We will also conduct outlier analyses. Statistical outliers will not be automatically removed from the data set but rather flagged, checked for accuracy, and corrected as needed. If and when data are deemed to be unusable they will be dropped, although this will be avoided whenever possible to maintain the integrity of the design.
Baseline Differences. Random assignment of classrooms should generate equivalent pre-intervention study groups, although sampling error and pre-test attrition may undermine this in the analytic sample. This in turn can yield biased estimates of the intervention’s impacts; it is therefore necessary to assess such equivalence and make corrections, as needed, during outcome analyses. If baseline differences are found on observable characteristics, they will be controlled by including these characteristics as covariates (at the appropriate level) in the multi-level models used to estimate impacts.
Baseline equivalence of the analytic sample will be assessed by comparing Odyssey® Math and control classrooms on the following: mean pretest at the classroom level, proportion of ethnicity/minority, proportion of free or reduced-price lunch status, proportion of special needs students, and proportion of English language learners. The following teacher characteristics will also be compared across conditions: years of teaching experience, level of education, number of hours of professional development in mathematics instruction (during the past year), and number of hours of professional development in using computer-technology to teach (during the past year).12 Differences between the two study groups will be tested using independent-samples t-tests for continuous variables and large sample z-tests on proportions as appropriate. Group characteristics for which there are statistically significant differences, based on these tests, will be controlled for during the impact analyses by including the group characteristics as covariates in the multi-level models. Again, the purpose of these tests is to identify whether the intervention and control groups are statistically equivalent at baseline. Consequently we want to use liberal unadjusted tests (i.e., we will make no attempt to control for elevated Type 1 error).
Describing the Implementation of the New Curricula & Overview of Classroom Observation Plan
Odyssey® Math and control classrooms will be observed to document intervention implementation and the type of mathematics instruction used in the control condition. The focus of the observations will be on goals for the class period, student-teacher interactions, student-technology interactions, teacher role in the use of the software, and general classroom management. By conducting the observations of both the intervention and control classrooms, we will document the types of activities that are conducted by all teachers participating in the study. Observations of control classrooms will also help document if there are any differences between control classrooms in terms of whether teachers and students use any mathematics curriculum software at all. In short, we intend to provide descriptive information that will contextualize quantitative analyses of the intervention’s impact.
Observations will be conducted three times throughout the academic year. The first observation will be scheduled approximately three weeks after the initial implementation of the intervention. A second observation will be conducted mid-year, and the third will occur approximately three weeks prior to the post-test. Observers will be a combination of Lab Extension Specialists and field research coordinators, who are required to have some post-baccalaureate experience with schools.13 All observers will receive prior training on the critical elements of the software and broader intervention components, and proper use of the observation checklists.
Observing Intervention Implementation
Developer Rubric. CompassLearning has generated a rubric for documenting implementation of the curriculum software. Sample items include: orients students and self to hardware, answers students’ questions about lesson, uses assessments, controls sequence of activities to complement instruction, guides students through instructional program blending software components, and classroom activities (CompassLearning, Inc., 2003, p. 310-311).14 Elements of the rubric are being used to generate a checklist that will be used during classroom observations.
Software Logs. The fidelity observations of the intervention group will be enhanced through the use of computer log data from the Odyssey® Math Software. The logs (gathered electronically) will be used to track student use of the system to ensure that each student is participating for at least 60 minutes during each week. The logs will provide information on each student’s progress, the tasks they attempted, how well they completed them, and the time spent on each task. Schools will be asked to submit logs to study personnel on a bi-weekly basis (the effort involves downloading and emailing records). In addition, schools will designate a contact person who will maintain weekly correspondence with the vendor to troubleshoot any technology problems. These records will also be submitted to the research team at regular intervals throughout the study so that we can address any unusual problems that would adversely affect the impact analyses (i.e., ones that occur outside of normal use of Odyssey® Math, such as school-wide computer viruses). This will also allow us to document the presence of any disruption or history effects.
Observing Control Classrooms
Observers will document the mathematics instruction in control classrooms using a modified version of the Standards Observation Form (Stonewater, 1996). The form will be used to document mathematics instruction and to assess the degree to which classroom instruction is consistent with the National Council of Teachers of Mathematics (NCTM) standards (See Exhibit J). Math content experts at Penn State have updated the form to address NCTM revisions that have taken place since the original checklist was developed ten years ago. The form will also be used to document math instruction in treatment classrooms when Odyssey® Math is not being used to better understand instructional context. Finally, the updated form will be altered so that it can check for the use of Odyssey® Math software in control classrooms to check for (the unlikely occurrence of) contamination.
Estimating the Effects of Odyssey® Math on Student Achievement: Multi-level Analyses and Impact Estimates
To address the research questions for this study, we specify three HLM models that will be estimated during the analysis phase using data collected from the study. For the readers’ convenience, we reiterate each research question and discuss the models that will be estimated to address it.
Question 1. Do Odyssey Math® classrooms outperform control classrooms on the mathematics subtest of the Terra Nova CTBS Basic Battery?
To address this question, a multi-level model (with students at level 1, classrooms at level 2, and school at level 3) will be used to compare the outcomes of students in the Odyssey® Math classrooms with comparison classrooms. The level 1 model is unconditional and is specified as follows:
Level 1 (student level):
Yijk= 0jk + rijk
where,
Yijk is the outcome for student i in class j in school k;
0jk is the average outcome of students in class j in school k;
rijk is a random error associated with student i in class j in school k; rijk ~ N (0, σ2).
The classroom average outcome estimated from the above model (i.e., level 1 intercept π0jk) will be modeled as varying randomly across classrooms and as a function of the intervention at level 2, the classroom level, controlling for the classroom average pre-test and the baseline covariates for which there is a statistically significant imbalance at the classroom level. The inclusion of these covariates should yield improved statistical precision of the parameter estimates (Bloom, Hayes, & Black, 2005; Raudenbush, Martinez, & Spybrook, 2005). The level 2 specification is as follows:
Level 2 (classroom level)
π0jk
= 00k
+ 01k*(Odyssey)jk
+ 02k*(Pretest)jk
+
![]() +
r0jk
+
r0jk
where
00k is the average student outcome across all classrooms in school k;
01k is the difference in student outcome between the Odyssey classrooms and the comparison classrooms (i.e., intervention effect) in school k;
Odyssey is an effect indicator variable for the intervention: ½ = Odyssey, and -½ = comparison;
02k, is the effect of mean class pre-test on classroom average student outcome in school k;
0pk, is the effect of the pth baseline characteristic for which there is a statistically significant pre-intervention imbalance on classroom average student outcome in school k;
r0jk is a random error associated with classroom j in school k on classroom average student outcome; r0jk ~ N (0, τπ00).
Pretest is the classroom average pretest score, grand-mean centered.
BICp is the pth baseline characteristic (or variable), for which there is a group imbalance of classroom average student outcome in school k, grand-mean centered if the characteristic is measured on a continuous scale or dummy coded if it is categorical. Statistical significance of each covariate will be re-examined in the model and non-significant covariates will be removed to obtain a parsimonious model.
In the level 3 model, both the school average outcome and the Odyssey® Math impact within each school (00k and 01k), estimated from the classroom-level model, will be modeled as random effects, assuming that both the classroom average achievement and the Odyssey effect differ systematically across schools (the Odyssey effect will be re-estimated as fixed effect if the variance of the coefficients is not significantly different from zero). Assuming that the coefficients for classroom average pre-test and the other covariates are homogenous across schools, the effects of pretest and other covariates will be fixed at the school level, as shown in the following specification:15
Level 3 (school level)
00k = 000 + u00k
01k = 010 + u01k
02k = 020
0pk = 0p0
where,
000 is the adjusted average student outcome across all schools;
u00k is a random error associated with school k on adjusted school average student outcome; u00k ~ N (0, τβ00);
010 is the average Odyssey effect across all schools after controlling for differences in pretest and the other covariates;
u01k is a random error associated with school k on the Odyssey impact; u01k ~ N (0, τβ11); and
020 is the average effect of pretest on the student outcome across all schools after controlling for differences in other covariates.
0p0 is the average effect of the pth baseline characteristic for which there is a statistically significant imbalance on the student outcome across all schools after controlling for differences in other covariates.
Of primary interest among the level 3 coefficients is 010, which represents the intervention’s main effect on the outcome across all schools. A statistically significant positive value of 010 will confirm the hypothesis that students in the Odyssey classrooms demonstrate higher levels of mathematics achievement than their counterparts in the comparison classrooms. The interpretation of the intervention’s effect, however, might need to be qualified. This depends on whether there is a significant amount of variation of the effect across schools as indicated by a statistically significant value of τβ11, which would suggest that the intervention has different effects in different schools rather than having a common effect across all schools. The level 3 residuals for the intervention effect generated from the above model (u01k) will further reveal those schools in which Odyssey has a particularly strong effect, and those schools in which Odyssey has a limited or no effect.
In addition to the statistical significance of Odyssey effect, we will also gauge the magnitude of the effect with the effect size index. Specifically, we will compute the effect size as a standardized mean difference (Hedges’ g) by dividing the adjusted group mean difference (010) by the unadjusted pooled within-group standard deviation of the outcome measure. It is possible that the intervention will impact only the treatment group standard deviation. In this case, Glass’ Delta (adjusted group mean difference divided by the control group standard deviation) may be a better metric although it utilizes less information because it does not consider treatment group variance (Lipsey & Wilson, 2001). Large differences between the two would indicate a differential impact on variance between treatment and control groups and this could provide additional information about the intervention. If this occurs, we will report the delta statistic.
Question 2. What is the effect of Odyssey® Math on the math performance of males and female students?
Odyssey® Math may have a differential impact on male and female students, which can be tested through a slopes-as-outcomes HLM model. The level 1 model is now specified as a function of gender:
Level 1 (student level)
Yijk = π0jk + π 1jk*(Gender)ijk + eijk
Where,
1jk is the gender gap on student outcome in class j in school k (i.e., mean difference in outcome between male and female students);
Gender is dummy-coded (1=male student, 0=female student);
All the other terms remain the same as those presented previously.
In the level 2, classroom-level model, the level 1 intercept is modeled the same way as that presented in the previous section. Level 1 slope for gender is modeled as a function of Odyssey to examine the cross-level interaction between Odyssey and gender. The level 2 equations are specified as follows:
Level 2 (classroom level)
π0jk
= 00k
+ 01k*(Odyssey)jk
+ 02k*(Pretest)jk
+
![]() +
r0jk
+
r0jk
π1jk = 10k + 11k*(Odyssey)jk + r1jk
where,
10k is the average gender achievement gap across classrooms in school k;
11k is the difference in the gender achievement gap between the Odyssey® Math classrooms and the comparison classrooms in school k;
r1jk is a random error associated with classroom j in school k on the achievement gap between gender; r1jk ~ N (0, τπ11); and
all the other terms remain the same as those presented previously.
The two level 2 parameters associated with gender gap within schools (10k and 11k), together with the school average outcome and the Odyssey® Math impact within each school (00k and 01k), will be modeled as random effects at the school level. The Odyssey effect on gender achievement gap or average class outcome will be re-estimated as a fixed effect if the variance of the coefficients is not significantly different from zero. As previously stated, the coefficients for covariates are assumed to be homogenous across schools (again, this assumption can be assessed by specifying the covariates as random effects and testing whether the variances of the coefficients across schools are zero; if a variance component is significantly different from zero, then the covariate will be treated as a random effect; otherwise, it will remain a fixed effect). Under the homogeneity of coefficients assumption, level 3 equations are specified as follows:
Level 3 (school level)
00k = 000 + u00k
01k = 010 + u01k
02k = 020
0pk = 0p0
10k = 100 + u10k
11k = 110 + u11k
where,
100 is the average gender achievement gap across schools;
110 is the average difference between Odyssey® Math and comparison classrooms in the
gender achievement gap across all schools;
u10k is a random error associated with school k on average gender achievement gap;
u11k is a random error associated with school k on the difference between Odyssey® Math and comparison classrooms in the gender achievement gap; u10k and u11k ~ N (0, Tβ); all the other terms remain the same as those presented previously.
In the above achievement gap analysis, the intervention’s main effect on student achievement is still represented by coefficient 010, as in the previous HLM model. The coefficient of particular interest in the gap analysis is 110, which represents the intervention’s main effect on the gender achievement gap across schools. A statistically significant value of 110 indicates that Odyssey® Math has a significant impact on the gender achievement gap, suggesting that boys and girls benefit differently from the intervention. Again, Odyssey® Math’s main effect on the gender achievement gap needs to be interpreted with caution—if the program’s effect on the gender achievement gap varies significantly across schools, as indicated by a significant value of the variance component.
Question 3. What is the effect of Odyssey Math on the math performance of low and medium/high achieving students (as measured by the pretest)?
Differential effects of Odyssey® Math for low achieving students and for medium/high achieving students will be examined. Students who scored at or below the third grade level on the Terra Nova pre-test will be designated on the subgroup variable as “low” achieving and those who scored above the third grade level will be designated as “medium/high” achieving. A dummy variable of achievement status will be created (1=low, 0=medium/high). The analytic model is the same as that for the gender analysis with the achievement status variable replacing the gender variable.
The interpretations of the coefficients in the model are similar to those in the previously described HLM analyses. The coefficient of primary interest is still 010, which represents Odyssey® Math’s main effect on the outcome across all schools. The coefficient of particular interest in the achievement gap analysis is 110, which represents the intervention’s main effect on the low-medium/high achievement gap across schools. A statistically significant value of 110 indicates that Odyssey® Math has a significant impact on the low-medium/high achievement gap, suggesting that low achieving students and medium/high achieving students benefit differently from the intervention. In addition, it is important to examine the value and statistical significance of the school-level residual variance of u11k to understand the extent to which the intervention effect on low-medium/high achievement gap varies across schools.
Plan for Managing Attrition (Teacher and Student) and Missing Data
General Approach. Attrition of teachers is problematic because it reduces power and can bias results. Randomization equalizes treatment and control groups at baseline (on expectations and in the long run), and this equivalence is expected to hold true for post-tests as well. Post-assignment attrition, however, may distort the pre-test equivalence, because attrition rarely is totally random. Attrition will be a serious problem in the study if teachers’ likelihood of dropping out of the study can be linked either to the treatment or observed outcome variables. Our plan to manage attrition includes four stages: prevention, reporting attrition, classifying attrition, and bias reduction with intent-to-treat analyses.
Prevention. The best solution to attrition is prevention. We are taking the following steps to prevent attrition in our study:
Clear explanation of study requirements to ensure that participating principals and teachers (schools) fully understand the burden created by study participation;
Use of monetary incentives to compensate teachers for the time used to complete surveys
We will also emphasize the importance of participating in this study, where results will not only be relevant for the participating teachers, but potentially for all educators teaching fourth grade mathematics.
Reporting. We will take the following steps to record attrition in the study:
Monthly phone calls to schools and the Odyssey® Math vendor inquiring whether any fourth grade teachers have applied for transfer/will be transferred, leave, or quit, and reasons for these actions, if available.
Record the number of teachers leaving/entering across comparison and treatment groups to detect differential attrition.
Classifying. Once attrition is properly recorded, we will conduct descriptive analyses to determine whether attrition in general, or certain patterns of attrition over time, can be linked to any teacher background characteristics. For instance, we will test whether inexperienced teachers leave from the study more often than more experienced teachers. These descriptive analyses will be conducted for the whole sample and by intervention and control group to detect differential attrition.
Intent To Treat. Teachers (and their classroom sections) who drop out of the study will be asked to complete the post-tests. If teachers (and their classroom sections) refuse to participate in the post-tests, three analytical options are available and each will be used:
Posttest scores at the teacher and student level will be imputed using multiple imputation (Rubin, 1981). Allison (2001) has shown that multiple imputation is a superior method to mean imputation, and is now a computationally accessible technique.
As an alternative we could set the missing values to the pretest value, rather than impute them (this approach conservatively assumes no change in student achievement from pre to posttest). The downside to this approach is that, depending on the number of missing values, the variance of the impact estimates could be restricted or downwardly biased.
Use listwise deletion and therefore omit the teacher and student observations with the missing values from the impact analysis using the HLM models.
A sensitivity analysis will be conducted by estimating impacts using the three above approaches and examine how sensitive these estimates are to each. The recommended course of action will be based on these results.
Managing Student-level attrition
The unit of random assignment is the classroom. The intervention takes place during a single academic year and power analyses allows for 20 percent student-level attrition. Therefore, student-level attrition is of limited concern unless an improbable and unexpected event occurs during study implementation that causes attrition to be severe (i.e., greater than 20%). We plan to interview teachers within the allotted time for the final classroom observation thereby reducing the burden on the teacher. Therefore this burden is included in the estimates presented earlier. Results from the interview will be used to document reasons for student attrition and code for whether teachers believed it was related to the study conditions or more common student mobility. Students who enter the treatment classrooms late during the school year will be included in our intent-to-treat sample. We will also consider analysis based on the dosage or length of the time students have stayed in the classrooms, excluding students who enter late during the school year from the analysis sample.
Tabulation of Study Results
We plan to present gamma coefficients, their standard errors, t-values, and p-values for the fixed effects for each model as shown in Table 5. We will also report estimates of variance components and their related test statistics (i.e., chi-square values, their degrees of freedom, and p-values; in the event SAS proc mixed is used, testing variance components will be based on large sample Z-tests). Intraclass correlations (ICC) will be reported for the unconditional model as well as for the conditional models.
Table 5
Random-Coefficient Model of Odyssey Math® Impacts on Math Achievement for Three HLM Models16
Fixed Effect |
Coefficient |
se |
t Ratio |
p Value |
Effect Size |
1. Average Odyssey effect across all schools17: 010 |
|
|
|
|
|
2. Average difference between Odyssey® Math and comparison classrooms in the gender achievement gap, across all schools: 110 |
|
|
|
|
|
3. Intervention’s main effect on the low-medium/high achievement gap across schools: 110 |
|
|
|
|
|
Random Effect |
Variance Component |
df |
X2 |
p Value |
|
1. Level-3 residuals for the intervention effect: u01k |
|
|
|
|
|
2. random error associated with school k on average gender achievement gap: u10k |
|
|
|
|
|
2. random error associated with school k on the difference between Odyssey® Math and comparison classrooms in the gender achievement gap: u11k |
|
|
|
|
|
3. random error associated with school k on average low-medium/high achievement gap: u10k |
|
|
|
|
|
3. random error associated with school k on the difference between Odyssey® Math and comparison classrooms in low-medium/high achievement gap: u11k |
|
|
|
|
|
As noted above, we will estimate treatment impacts using either pooled or control group standard deviations, or both. Pooled standard deviation can be obtained by taking the square root of the unadjusted student level variance pooled across treatment and control groups. Control group standard deviation is simply the standard deviation of the criterion measure for students assigned to the control condition. Student level standard deviations will be used because impact estimate at the student level is the most common interpretation audiences might have (i.e., the impact of the treatment at the student level).
Furthermore, the use of level-1 student variance should yield more conservative estimates given student-level variance will be larger. When there are more than one significant random variance components, correlations among the random effects will also be reported. The following table represents how we plan to present the data from the three models, based on the research questions (modified from Raudenbush & Bryk, 2002, p. 122). Statistics associated with Odyssey Math effect will be reported for all three models (1 through 3).
Publication Plans and Time Schedule
The REL will report findings to IES in the annual report with interim findings reports after school recruitment, beginning implementation, in December 2007(in the middle of the implementation year), at the end of the year and after the data analysis is completed. If there are delays in the school recruitment and the team is allowed a phased implementation, we will provide reports during the two year implementation timeframe.
IES report. A final technical report for the study will be submitted to IES for review. The final report will be reviewed by the REL TWG prior to submission to IES. As noted in section 12.3, we will coordinate with IES and the National Lab Network to determine how to disseminate the report. Multiple products will be created and various dissemination channels will be utilized dependent on the relevant target audience identified for each product. A product announcement will be developed prior to the start of the study and periodic interim research bulletins will be created and distributed throughout the life of the study.
Peer-reviewed journals. Members of the study team may, per any relevant IES guidelines, submit articles to peer-reviewed journals, though specific results of the current study will first have to be disseminated to IES.
Conference Presentations. Members of the study team may submit proposals for conference presentations subject to appropriate IES guidelines and contract restrictions. Presentations of preliminary data may be made at national scholarly conferences pending approval by the lab.
TABLE 6
SCHEDULE OF ACTIVITIES
Activity |
Schedule |
Interim Report to IES – Recruitment & Beginning Implementation |
12/2007 |
Interim Report to IES – Phase 1* |
9/2008 |
IES Draft of Final Report |
1/2009 |
Conference Presentations |
After approval of IES report |
Peer reviewed journals |
After approval of IES report |
* Assumes only one randomization phase is utilized. If two are needed, a phase 2 interim report will be provided in 9/09 and add one year to each date above.
Approval Not to Display the Expiration Date for OMB Approval
All data collection instruments will include the OMB expiration date.
Exception to the Certification Statement
No exceptions are requested.
References
Agodino, R., Dynarski, M., Honey, M., & Levin, D. (2003, May). The effectiveness of educational technology: Issues and recommendations for the national study. (Available from Mathematica Policy Research, Inc., P.O. Box 2393, Princeton, NJ, 08543-2393)
Allison, P. D. (2001). Missing data. Sage University Papers Series on Quantitative Applications in the Social Sciences, 07-136. Thousand Oaks, CA: Sage.
Bloom, H.S. (Ed.) (2005). Learning more from social experiments: Evolving analytic approaches. New York: Russell Sage.
Bloom, H.S., Richburg-Hayes, L., & Black, A.R. (2005). Using covariates to improve precision: Empirical guidance for studies that randomize schools to measure the impacts of educational interventions . New York: MDRC.
Boruch, R.F. (1997). Randomized experiments for planning and evaluation: A practical guide. Thousand Oaks, CA: Sage.
CompassLearning, Inc. (2003). CompassLearning® report: What Works Clearinghouse. San Diego, CA: CompassLearning.
CTB/McGraw-Hill (2000). TerraNova: Frequently Asked Questions, Monterey, CA: Author.
Flay, et al. (2005). Standards of evidence: Criteria for efficacy, effectiveness, and dissemination. Prevention Science, 1-23.
Lipsey, M.W. & Wilson, D.B. (2001). Practical meta-analysis. Thousand Oaks, CA: Sage.
Mosteller, R., & Boruch, R. (Eds). (2002). Evidence matters: Randomized trials in education research. Washington, DC: Brookings Institution Press.
National Council of Teachers of Mathematics (1998). Principles and standards for school mathematics: Discussion Draft. Reston, VA, author.
National Council of Teachers of Mathematics (1989). Curriculum and evaluation standards for school mathematics. Reston, VA, author.
Orr, L. (1998). Social experiments: Evaluating public programs with experimental methods. Thousand Oaks, CA: Sage.
Raudenbush, S.W., & Bryk, A.S. (2002). Hierarchical linear models: Applications and data analysis methods (2nd ed.). Thousand Oaks, CA: Sage Publications, Inc.
Raudenbush, S.W., Martinez, A., & Spybrook, J. (2005). Strategies for improving precision in group-randomized experiments. New York: William T. Grant Foundation
Rubin, D. B. (1981). The Bayesian bootstrap. Annals of Statistics, 9(1), 13-134.
Schochet, P.Z. (2005). Statistical power for random assignment evaluations of education programs. Princeton, NJ: Mathematica Policy Research.
Shadish, W.R., Cook, T.D., & Campbell, D.T. (2002). Experimental and quasi-experimental designs for generalized causal inference. Boston: Houghton Mifflin.
Sniders, T., & Bosker, R. (1999). Multilevel analysis: An introduction to basic and advanced multilevel modeling. London: Sage Publications.
Stonewater, J.K. (1996). The Standards Observation Form: Feedback to
teachers on classroom implementation of the Standards. School Science
and Mathematics, 96(6), 290-297.
Appendices
Appendix A
Computer Requirements for Use of Odyssey Math
Odyssey Math Computer Requirements:
Information in this document is currently, however CompassLearning cautions that on-going industry innovation may yield changes.
Odyssey PreK- 8 Browser Based Workstation Requirements July 2006
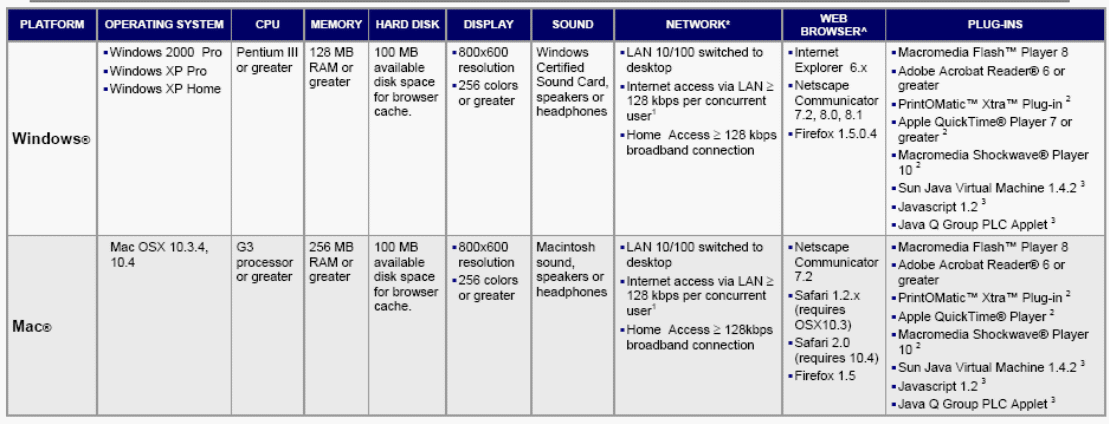
Odyssey PreK-8 Print and Scan Option: Scantron scanner available through CompassLearning.
Notes
1 T-1 = 8 - 16 concurrent users, dependent upon available bandwidth and curriculum chosen. Call for consultation or request a site assessment.
2 Required to run Pre-K learning activities.
3 Required for ELL content
• Odyssey requires Pop-up blockers be turned off for the Odyssey site.
• Ports 80 and 443 (SSL Encryption) must be open at the firewall.
• Specific browser settings and additional configuration combinations can be found on the Systems Requirements page at http://www.compasslearningodyssey.com/systemrequirements.html
• Odyssey PreK-8 may require web caching to enhance performance and increase the number of concurrent users. See a CompassLearning representative.
• Odyssey PreK-8 Enterprise: The Odyssey Writer curriculum stores student work portfolios, allow a minimum of 25 MB per school. Additional space may be required dependent on use model.
• Odyssey PreK-8 Hosted: For Odyssey Writer, 25 MB of online disk storage is available per school. Additional storage is available at additional cost. Contact a CompassLearning sales representative.
CompassLearning Odyssey PreK-8 Bandwidth Requirements and Considerations July 2006
BANDWIDTH |
|
NETWORK |
Bandwidth Considerations
Slow or congested network connections using Odyssey PreK-8 will require web caching and will support a limited number of concurrent users.
|
ODYSSEY AND WEB CACHING SERVERS |
Web Caching Recommended To enhance web performance and preserve bandwidth, deployment of a Web caching for Odyssey PreK-8 is appropriate for some infrastructures that do not have adequate bandwidth. Advantages of Web Caching :
Reduced server load (fewer requests for the Odyssey server to handle)
|
WEB CACHE SERVER/APPLIANCE SPECIFICATIONS |
Odyssey K-8 is designed from the ground as a browser based application. By design 80% of Odyssey’s content is cacheable. Implementing a web caching strategy in your network infrastructure will speed the delivery of the content to your students, while effectively utilizing the available bandwidth.
|
WIRELESS 802.11a/g NETWORK |
The number of concurrent users is dependent upon the network speed, environment and number of users per access point. |
Appendix B
CompassLearning Web-Based Resources and Peer Support
Appendix C
Intermediate Units in Pennsylvania
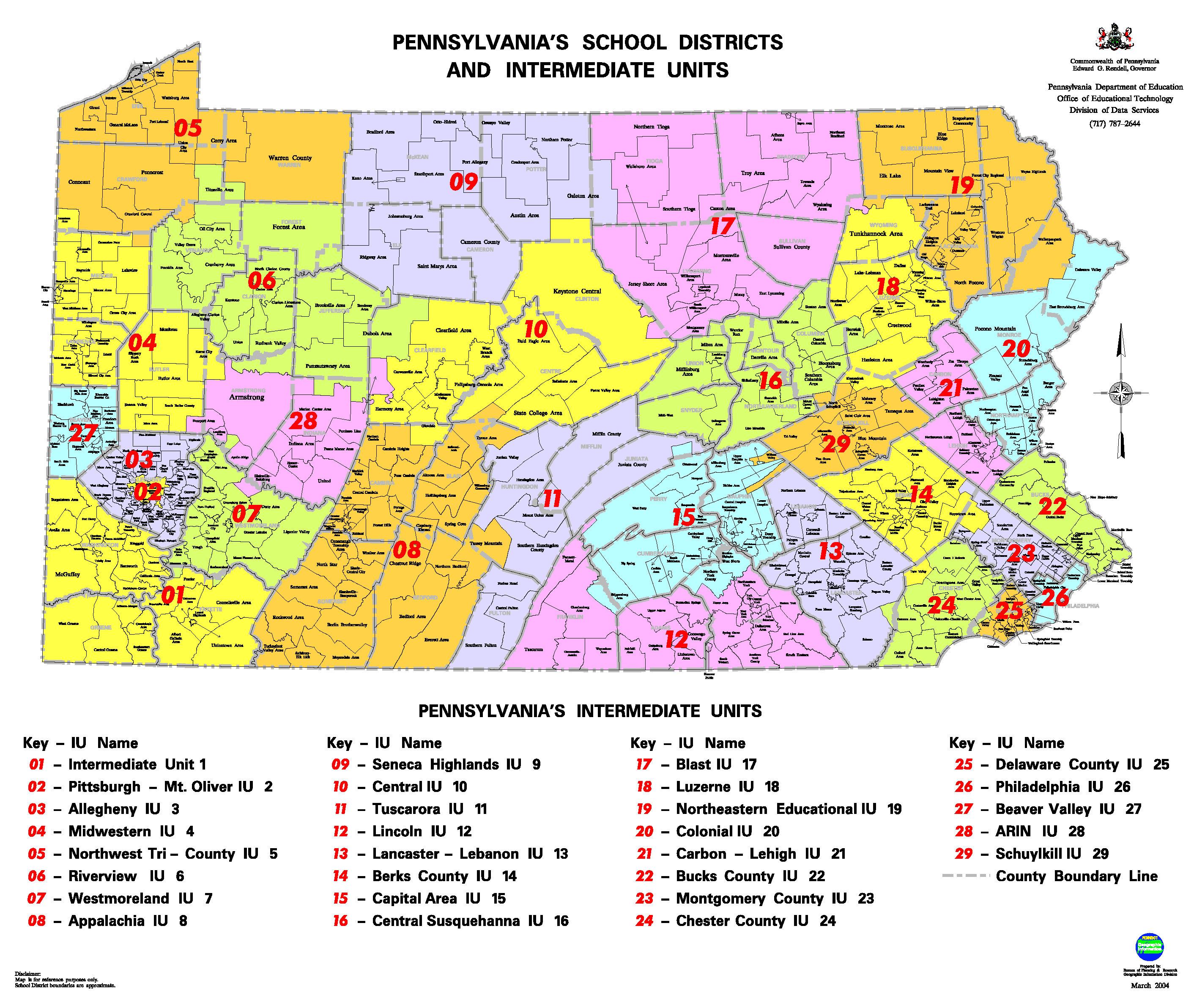
Appendix D: Flow of Classrooms and Student from Baseline through Reporting
Odyssey
Math Implementation
Instruction
as Usual Implementation
Odyssey
Math Implementation
Instruction
as Usual Implementation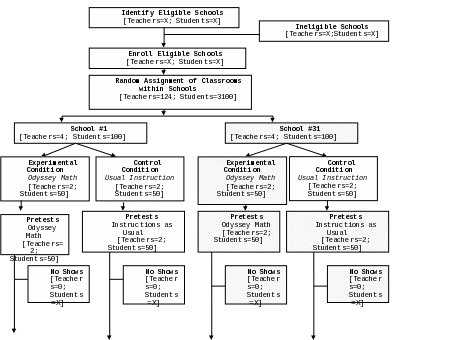

[Teachers=2;
Students=X]
[Teachers=2;
Students=X]




[Teachers=2;
Students=X]
[Teachers=2;
Students=X]
Posttests
Posttests
Drop-outs
Drop-outs
Drop-outs




[Teachers=2;
Students=20]
[Teachers=2;
Students=20]

[Teachers=0;
Students=X]


[Teachers=0
; Students=X]

[Teachers=0;
Students=X]








Analysis
Report
Drop-outs
Posttests
Posttests
* Please note that numbers
of schools, teachers, and students used here are based on the
assumption shown in Table 1b.
[Teachers=124;
Students=2480]
[Teachers=124;
Students=2480]
[Teachers=0;
Students=X]
[Teachers=2;
Students=20]
[Teachers=2;
Students=20]
1 For reasons noted below, the study may extend to 2008-2009.
2 Effect sizes were calculated by taking the difference between the percentages of students rated at or above proficient in the two years, and dividing that by the standard deviation on the students' test scores, which resulted in reported effect sizes as high as 5.0 in math and 5.4 in language arts.
3Low achieving students are defined as ones who score at the third grade level or below on the Terra Nova at pretest. Students who score above this point are in the medium/high achieving category.
4 Given the timing of this submission it may not be feasible to recruit the full sample by next academic year. We therefore have a contingency plan; if necessary we will begin the study with a partial sample starting next academic year, and complete the work in the 2008-2009 year. More details are below.
5 Allow for possible use of a phased recruitment and a randomization plan spanning two years.
6 We will include a hardcopy backup for teachers in the control group who will not have access to the web-survey conducted during the summer training for the intervention teachers.
7 CTB/McGraw-Hill (2000). TerraNova: Frequently Asked Questions, Monterey, CA: Author.
8 The test developer recommends that there be at least six months between a pre-test and a post-test administration. Additional documentation (e.g., a memo from Dr. George Burket, dated February 16, 1999, concerning recommended minimum intervals between pre-test and post-test) is available from the developer upon request.
9 The 2005 norms are an update of the published 2000 norms using a combination of the 2000 standardization data and customer data from 2001 and 2005 to adjust for the two factors: (1) the changing demographic composition of the national school population, and (2) the instructional intervention programs that have altered student performance since observed in 2000.
10 TerraNova Basic Battery Form A is a copyrighted document and is considered proprietary, and thus, is not included in this document. Note that we have permission to use the test.
11 For this reason, the below section describing the HLM models in detail are somewhat repetitive; a truncated version of the third model is offered.
12 School archival data will be used to obtain classroom characteristics. Teachers will be asked to fill out a brief survey (See Exhibit F) at the start of the school year (or during Odyssey Math summer training if the teacher is in the intervention condition).
13 As noted below, Lab Extension Specialists (LESs) typically have extensive K-12 experience.
14 This is an assessment technique used within the intervention to monitor student progress. It is not an outcome measure.
15 This assumption can be assessed by specifying the covariates as random effects and testing whether the variances of the coefficients across schools are zero; if a variance component is significantly different from zero, then the covariate will be treated as a random effect; otherwise, it will remain a fixed effect.
16 Specified as HLM Models 1, 2, 3 for the Three Research Questions
17 The numerical indictor corresponds with the HLM model and research question. Here, the number 1 refers to the gamma associated with the question 1. The next row is associated with question 2 (gender).
| File Type | application/msword |
| File Title | MEMORANDUM |
| Author | Temporary Secretary 1 |
| Last Modified By | DoED |
| File Modified | 2007-03-28 |
| File Created | 2007-03-28 |
© 2025 OMB.report | Privacy Policy

