Supporting Statement_PartB_Ohio Shipper Survey 5-22-19
Supporting Statement_PartB_Ohio Shipper Survey 5-22-19.doc
2019 Agricultural Shipper Transportation Needs Survey: Ohio River System
OMB: 0710-0022
SUPPORTING STATEMENT – PART B
U.S. Army Corps of Engineers
Ohio River Shipper Response Survey - OMB 0720-XXXX
If the collection of information employs statistical methods, it should be indicated in Item 17 of OMB Form 83-I, and the following information should be provided in this Supporting Statement:
Description of the Activity
The target population for this collection are agricultural grain shippers located in the Ohio River Valley and within 200 miles of the Ohio River. Based on previous research and supplemental material this region should capture most, if not all, agricultural shippers that use or potentially use the Ohio River for waterway shipments.
USDA estimates a population of 1958 locations in PA, OH, IN, IL, KY, TN, and WV. A list of facilities, with a focus on grain elevators and warehouses, has been developed from USDA, Waterborne Commerce Port Series, on-line search, State Departments of Agriculture, Grain Association Directories, lists compiled by other organizations (Upper Great Plains Transportation Institute), and other sources from previous studies and includes contact information. This list has 1487 locations, and after omitting shippers located more than 200 miles from the Ohio River reduces the number to 1,174 shippers in the study region. All 1,174 shippers will be contacted.
The survey will proceed with direct mail providing a web-link. Non-respondents will be contacted by email (if an address is available) three days later, and postal letter with a weblink and a questionnaire on day 7. This will be followed a week later (day 14) with a post card reminder. One to two weeks later (days 21-35), non-respondents will be contacted by telephone, and finally on day 42, non-respondents will be sent a letter and questionnaire. Exhibit 1 provides a summary of expected response rate by administration stage. The expected response rate is based on previous surveys that are similar. Hence, we expect a total of 352 responses upon completion of several iterations.
Administration Stage |
Sample |
Anticipated response |
1. Initial contact, web survey invitation |
1,174 |
81 |
2. First mail questionnaire with cover letter packet, |
993 |
15 |
3. Reminder postcard |
978 |
6 |
4. Telephone contact with follow-up e-mail/letter |
932 |
230 |
5. Final Reminder |
702 |
20 |
TOTAL |
352 |
|
Exhibit 1: Response by Administration Stage
Procedures for the Collection of Information and estimation procedures.
The population and sampling methodology are described in item 1 above.
Estimation procedures
There are two primary models that are to be estimated with the data. These are: a choice model which is based on a Random Utility Model and Tobit model of annual volumes. Each is discussed in turn.
Random Utility Mode – Mode/Destination Choice
The survey solicits information on the last shipment made. The information include the mode/destination choice of the shipper and alternative mode/destination choices that could have been made. These “revealed” data are supplemented by “stated preference” data wherein shippers are prompted with changes in rate, transit times and reliability and asked if they would switch to the alternative or not. Estimation is somewhat complicated by the fact that the stated preference data are based on the revealed choice. Train and Wilson (2008) developed and published a procedure (which has been used in multiple studies) to handle the estimation and that procedure is planned for this study under different assumptions relating to the treatment of heterogeneous responses of shippers with regard to changes in the variable (rate, time and reliability). In particular, the model will be estimated given symmetric responses (a fixed coefficient model) and for asymmetric responses (a mixed logit model). The result is used to calculate shipper responses to changes in rates, transit time, and reliability.
The
basic model is a random utility model where in shippers choose the
mode and the destination of a shipment based on utility. With fixed
coefficients, the shipper’s choice in the revealed preference
setting is a standard logit model. The
shipper faces J
alternatives for its last shipment. The utility of each alternative
depends on observed variables, namely, rate, transit time, and
reliability, as well as unobserved factors.1
The observed variables are denoted xj
for alternative j
(with the subscript for the shipper omitted for simplicity), and the
unobserved random factors are denoted collectively εj
as for alternative j.
Utility of alternative j
is denoted Uj=βxj+εj.
Under the assumption that each εj
is distributed iid extreme value, the probability that the shipper
chooses alternative i
is the logit formula
 and the parameters are estimated
with maximum likelihood.
and the parameters are estimated
with maximum likelihood.
The revealed preference data can and will be appended to include stated preference responses. Specifically, in the survey, shippers are presented with a series of stated preference questions that are constructed on the basis of the shipper's rp choice.
Generally,
there are T
sp-off-rp questions, with attributes
![]() for alternative j
in question t based
on alternative i
having been chosen in the rp setting. For the questions soliciting
sp responses, the attributes of the rp setting are perturbed to
confront the shipper a change in the utility of the rp choice. The
attributes of the sp are given by
for alternative j
in question t based
on alternative i
having been chosen in the rp setting. For the questions soliciting
sp responses, the attributes of the rp setting are perturbed to
confront the shipper a change in the utility of the rp choice. The
attributes of the sp are given by
![]() and
and
![]() for the alternative that was chosen in the rp setting. The shipper
is asked to choose among the alternatives in response to each
sp-off-rp question. The shipper's choice can be affected by
unobserved factors that did not arise in the rp setting, reflecting,
e.g., inattention by the agent to the task, pure randomness in the
agent's responses, or other quixotic aspects of the sp choices.
These factors are labeled as
for the alternative that was chosen in the rp setting. The shipper
is asked to choose among the alternatives in response to each
sp-off-rp question. The shipper's choice can be affected by
unobserved factors that did not arise in the rp setting, reflecting,
e.g., inattention by the agent to the task, pure randomness in the
agent's responses, or other quixotic aspects of the sp choices.
These factors are labeled as
![]() for alternative j.
The relative importance of these factors will be estimated, as
described below. The shipper obtains utility
for alternative j.
The relative importance of these factors will be estimated, as
described below. The shipper obtains utility
![]() from alternative j
in sp-off-rp question t.
That is, the shipper evaluates each alternative using the same
utility coefficients and with the the same unobserved attributes as
in the rp setting, with the addition of new errors that reflect
quixotic aspects of the shippers’ responses to the sp-off-rp
questions. In response to each sp-off-rp question, the shipper
chooses the alternative with the greatest utility. To complete the
model, we assume that each
from alternative j
in sp-off-rp question t.
That is, the shipper evaluates each alternative using the same
utility coefficients and with the the same unobserved attributes as
in the rp setting, with the addition of new errors that reflect
quixotic aspects of the shippers’ responses to the sp-off-rp
questions. In response to each sp-off-rp question, the shipper
chooses the alternative with the greatest utility. To complete the
model, we assume that each
![]() is iid extreme value with scale 1/α,
which is proportional to the standard deviation of these errors. A
large value of parameter α
indicates that there are few quixotic aspects to the sp-off-rp
responses and that the shippers choose essentially the same as they
would in a rp situation under the new attributes. Utility can be
equivalently expressed as
is iid extreme value with scale 1/α,
which is proportional to the standard deviation of these errors. A
large value of parameter α
indicates that there are few quixotic aspects to the sp-off-rp
responses and that the shippers choose essentially the same as they
would in a rp situation under the new attributes. Utility can be
equivalently expressed as
![]() where
now
where
now
![]() is iid extreme value with unit scale. The sp-off-rp responses are,
therefore, standard logits with εj
as an extra explanatory variable. Since the εj
's are not observed, these logits must be integrated over their
conditional distribution, as follows. The chosen alternative in
response to question t
is denoted kt
and vector
is iid extreme value with unit scale. The sp-off-rp responses are,
therefore, standard logits with εj
as an extra explanatory variable. Since the εj
's are not observed, these logits must be integrated over their
conditional distribution, as follows. The chosen alternative in
response to question t
is denoted kt
and vector
![]() collects the sequence of responses to the sp-off-rp questions.
collects the sequence of responses to the sp-off-rp questions.
The probability of alternative kt in response to sp-off-rp question t, conditional on i being chosen in the rp choice is:
 This
probability is a mixed logit (Train, 2003), mixed over the
conditional distribution of
This
probability is a mixed logit (Train, 2003), mixed over the
conditional distribution of
![]() .
It can be simulated by taking draws from the distribution of ε,
calculating the logit formula for each draw, and averaging the
results.
.
It can be simulated by taking draws from the distribution of ε,
calculating the logit formula for each draw, and averaging the
results.
Draws
of ε
from its conditional density are easy to obtain, given the convenient
form of the conditional density of extreme value deviates (Train and
Wilson, 2008.) In particular, the density of εi
conditional
on alternative i
being chosen in the rp setting is extreme value with mean shifted up
by -ln(Pi).
A draw is obtained as -ln(Pi)-ln(-ln(μ))
where μ
is a draw from a uniform between zero and one. Conditional on εi
and on i
being
chosen, the density of each
![]() ,
is extreme value truncated above at
,
is extreme value truncated above at
![]() .
A draw is obtained as -ln(-ln(m(εi)μ)),
where μ
is a draw from a uniform between zero and one, and
.
A draw is obtained as -ln(-ln(m(εi)μ)),
where μ
is a draw from a uniform between zero and one, and
![]() Since
draws of ε
are constructed analytically from draws from a uniform (as opposed to
by accept-reject methods), variance reduction procedures can readily
be applied, such as Halton draws (Bhat, 2001, Train, 2003),
(t,m,s)-nets (Sandor and Train, 2003), and modified Latin hypercube
sampling (Hess et al, 2004.)
Since
draws of ε
are constructed analytically from draws from a uniform (as opposed to
by accept-reject methods), variance reduction procedures can readily
be applied, such as Halton draws (Bhat, 2001, Train, 2003),
(t,m,s)-nets (Sandor and Train, 2003), and modified Latin hypercube
sampling (Hess et al, 2004.)
Combining these results, and using the independence of ηjt over t, the probability of the agent's rp choice and the sequence of responses to the sp-off-rp questions is:

where
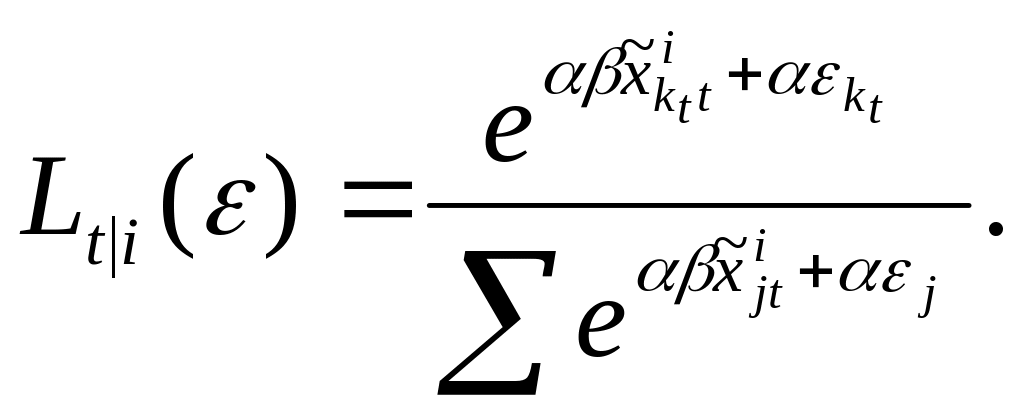
This probability is simulated by taking draws of ε from its conditional distribution as described above, calculating the product of logits within brackets for each draw, averaging the results, and then multiplying by the logit probability of the rp choice.
As a final investigation, shippers may differ in their responses. As is now becoming standard, heterogeneous responses can be accommodate with a mixed logit wherein the parameters of the utility function, β, is random with density h(β) that depends on parameters (not given in the notation) that represent, e.g., the mean and variance of β over shippers. The probability for the rp choice is the logit formula integrated over the density of β:
![]()
where

This
is a standard mixed logit. By Bayes’ rule, the density of β
conditional on i
being
chosen is
![]()
For
the responses to the sp-off-rp questions, let
![]() be
the same as
be
the same as
![]() defined
above but with β
treated as an argument. The probability of the sequence of responses
to the sp-off-rp questions is
defined
above but with β
treated as an argument. The probability of the sequence of responses
to the sp-off-rp questions is
![]()
![]() .
.
The probability of the rp choice and the sequence of responses to the sp-off-rp questions is Pi times the above formula, which is:
![]() .
.
This probability is simulated by:
Draw a value of β from its unconditional density.
Calculate the logit probabiliuty for the rp choice using this β.
Draw numerous values of ε from its conditional density given β using the method described above. Caluclate the product of logit formulas for the responses to the sp-off-rp questions for each draw of and average the results.
Multiply the result from step 3 by the result from step 2.
Repeat steps 1-4 numerous times and average the results.
In theory, only one draw in step 3 is required for each draw in step 1; however, taking more than one draw in step 3 improves accuracy for each draw of β and is relatively inexpensive from a computational perspective.
Tobit Model – Volume Responses
In
addition to the mode/destination choices described above. The
survey also provides information relating to the annual volumes
shipped. In this second empirical exercise shippers are asked to
provide annual volumes (Q0)
and then attributes i.e., price, rate, time and reliability are
perturbed to give a new setting. The initial annual volume is taken
as a function of price, rates, time and reliability. Each of these
four are randomly changed and shippers are asked to provide whether
they respond or not, and if they respond, how much they respond. The
empirical model estimated that has been used in previous studies
e.g., Train and Wilson (2008b) is based upon a Cobb-Douglas
specification of outputs given by:
![]() where
x
represents the attribute that is changed e.g., price, rate, time and
reliability, and r
represents
the other attributes. The idea is that as an attribute changes, the
annual volumes may change. Let
where
x
represents the attribute that is changed e.g., price, rate, time and
reliability, and r
represents
the other attributes. The idea is that as an attribute changes, the
annual volumes may change. Let
![]() represent
the percentage change in an attribute (say, x), the response then can
be written as:
represent
the percentage change in an attribute (say, x), the response then can
be written as:
![]() .
The empirical model obtained is:
.
The empirical model obtained is:
![]()
Where Q1 and Q0 are the annual volumes after a change in attributes, and before a change in attributes.
The
responses that have historically been obtained range from no change
i.e.,
![]() 0
to a 100 percent change e.g., if rates are increased enough, the
shipper may not longer ship. Such changes restrict the domain of the
dependent variable, but can be accommodated with a two-limit tobit
model, which is commonly used in such cases.
0
to a 100 percent change e.g., if rates are increased enough, the
shipper may not longer ship. Such changes restrict the domain of the
dependent variable, but can be accommodated with a two-limit tobit
model, which is commonly used in such cases.
Degree of accuracy needed for the Purpose discussed in the justification;
The survey responses will provide mode and destination as well as annual volumes data that will be used to estimate the choice model and the annual volumes model. An array of estimates e.g., shipper choice responses annual volume responses to changes in rates, transit time, and reliability can be formulated from the estimation results. The confidence levels for these estimates will likely vary with the type of estimate and with the precision of the associated model parameters. While the precision of these parameters is difficult to predict in advance, based on past experience with similar models, the study team believes that reasonably precise estimates can be obtained with 200 or more responses.
Unusual problems requiring specialized sampling procedures; and
There are no specialized sampling procedures used.
Use of periodic or cyclical data collections to reduce respondent burden.
This is a one-time survey and is therefore the most infrequent collection interval possible.
Maximization of Response Rates, Non-response, and Reliability
The population in this survey has only 1174 shippers. Several measures will be taken to encourage as high an initial response as possible, including:
Postal notification letter w/ weblink and access code including form for updating contact name and information for correct respondent for establishment; includes posted business reply (day 1)
Email reminder (if have email, day 3)
Postal letter w/ weblink and questionnaire (day 7)
Postcard reminder (day 14)
Telephone reminder with interviewers sending email w/ weblink & access code (day 21 to 35) or if requested mail questionnaire + letter
SESRC calling to remind nonrespondent to return questionnaire. Increase this sample size to all remaining nonrespondents
Increase number of call attempts to 8 for reminding nonrespondents. Collect eligibility information and recall any new identified respondents and sending emails with survey web link for the establishment.
Letter and mail questionnaire to non-respondents (day 42)
Despite these measures, response rates for the mail screener and telephone follow-up survey are unlikely to exceed 50%. This raises a concern of non-response bias as well as a lack of precision owing to small numbers of responses. In any survey, there are potential issues. These include an adequate number of responses, non-response bias, differences with respect to survey protocol. As noted above, the previous surveys with similar sample sizes as those expected have yielded statistically significant results on the key parameters estimated. Non-response bias is always a concern, but the contact list employed has some information which can be used to compare the attributes e.g., capacity, distance to the waterway between respondents and non-respondents. The survey uses a mixed mode approach as has been done in past surveys. The primary intent is to increase the number of responses. However, there can be differences among the respondents due to the mode used. Again, a comparison of attributes across survey mode will identify whether there are statistical differences in observed attributes. Finally, the questions asked in the survey have been used effectively in previous surveys. They have been pre-tested and refined many times in past surveys and in initial survey design efforts.
Tests of Procedures
The survey instrument used follows that used in numerous previous studies with only minor refinements to fit the target population. These have been pre-tested with interviews of shippers, industry specialist, and the survey team. Feedback from each were incorporated into the survey instrument for language, organization and clarity.
Statistical Consultation and Information Analysis
Provide names and telephone number of individual(s) consulted on statistical aspects of the design.
Wesley W. Wilson
University of Oregon
(541) 346 4690
Kenneth Train
Adjunct Professor, University of California-Berkeley.
(415) 291-1023
Eric Jessup
Associate Professor, School of Social Science, Washington State University
(509) 335-4987
Provide name and organization of person(s) who will actually collect and analyze the collected information.
Danna Moore (Social and Economic Sciences Research Center, Washington State University)
References
Bhat, C., 2001. Quasi-random maximum simulated likelihood estimation of the mixed multinomial logit model. Transportation Research
Part B 35, 677–693.
Sandor, Z., Train, K., 2004. Quasi-random simulation of discrete choice models. Transportation Research, Part B 38, 313–327.
Train, K. 2003. Discrete Choice Methods with Simulation, Cambridge University Press, New York.
Train, Kenneth, and Wesley W. Wilson (2008) “Estimation on Stated-Preference Experiments Constructed from Revealed-Preference Choices." Transportation Research – B, Vol. 42 (2008), 191-2003.
Train, Kenneth, and Wesley W. Wilson (2008b). "Transportation Demand and Volume Sensitivity: A Study of Grain Shippers in the Upper Mississippi River Valley." Transportation Research Record No. 2062. pp. 66-73.
1 The model is framed in a utility context although the term profit maximization can be employed so long as there are no agency issues i.e., the shipper makes decisions consistent with the firm’s objective of maximizing profit.
| File Type | application/msword |
| Author | Patricia Toppings |
| Last Modified By | SYSTEM |
| File Modified | 2019-09-30 |
| File Created | 2019-09-30 |
© 2026 OMB.report | Privacy Policy