ANI Content Assesment A

ANI Content Assessment

Form A

1. Nathaniel suggested the following idea for doing the problem:

0.23

x 95

First I ignore the decimal point and do the multiplication, which gives me 2185. Then I use estimation to place the decimal point. I know that 0.23 is about 1/4 and 95 is about 100 and 1/4 of 100 is 25, so my answer would be 21.85.

Which of the following is most appropriate to say about Nathaniel’s approach? (Circle ONE answer.)

1. It happens to work in this case, but will not always work.

2. It only works if one of the numbers is a whole number.

3. It works for any numbers, but some examples are harder to estimate.

4. It works equally well for all problems.

2. Mrs. Wise wants to include some word problems on her fractions quiz. Which of the following problems could she use as a word problem for – ? (For each item below, circle YES, NO, or I’M NOT SURE.)

		Yes	No	I’m not sure
I have of a pizza left. My brother comes in and eats of my leftover pizza. How much pizza is left?
Farmer Brown has plowed up of a field. He wants to plant of that half in corn. What fraction of the entire field will be planted in corn?
Mom has of a cup of sugar. She needs to use of a cup of sugar to make some brownies. How much sugar will Mom have left?

3. A group of Ms. Lee’s students was following a set of directions to move a paper frog along a number line.

Their last direction took them to . The next direction says:

Go of the way to . What number will the frog land on?

The students disagreed about where the frog would land. Which answer should Ms. Lee accept as correct? (Mark ONE answer.)

1. 

2. 

3. 

4. 

e)

f) I'm not sure.

4. Teachers often offer students “rules of thumb” to help them remember particular mathematical ideas or procedures. Sometimes, however, these handy memory devices are not actually true, or they are not true for all numbers. For each of the following, decide whether it is true all of the time or not. (Mark TRUE FOR ALL NUMBERS, NOT ALWAYS TRUE, or I’M NOT SURE.)

	True for all numbers	Not always true	I’m not sure
If the first of two numbers is smaller than a second, and you add the same number to both, then the first sum is smaller than the second.
Multiplying a number makes it larger.
A negative number plus another negative number equals a negative number.
To multiply any number by 10, add a zero to the right of the number.

5. Mrs. Jenson’s students are just beginning a unit on proportions. The students are using intuitive strategies, but have not yet learned the cross multiplication procedure. Which of the following problems is likely to be the most difficult at this point? (Circle ONE answer.)

a)

b)

c)

d) All problems provide the same level of difficulty.

6. Students in Mr. Castle’s classroom are trying to figure out the amount of profit they will make on the sale of 90 raffle tickets if they make $7 profit for every 15 tickets sold.

As Mr. Castle monitors the work of students in his class, he notices one of the groups had drawn the following table:

Amount of Profit	7	14	28
Number of Tickets	15	30	60

One of the students argued that since 30 + 60 = 90 (the number of raffle tickets sold) that the amount of profit would be 14 + 28 = 42.

What is true about the student’s approach to the problem? (Circle ONE answer.)

1. The method is incorrect, even though it happens to give the right answer for this problem. You cannot add when working with proportions.

2. The answer is actually wrong.

3. The method is correct, but might not generalize easily to other numbers of tickets sold.

4. This method only works when you add quantities next to one another in the table.

7. Ms. Green was writing a worksheet for her students. She wanted to demonstrate that some situations are modeled by proportional relationships and others are not. Which of the following problems models a proportional relation? (Circle PROPORTIONAL, NOT PROPORTIONAL, or I’M NOT SURE for each.)

	Proportional	Not proportional	I’m not sure
a) The population of a certain type of bacteria doubles every 6 hours. If there are initially two bacteria in the culture, what will the population be after 30 hours?	1	2	3
b) Sal bought three raffle tickets for $5. How many tickets can he buy at the same price for $55?	1	2	3
c) Theda has 5 pictures for her portfolio. If she draws three pictures each week, how many pictures will she have after 4 weeks?	1	2	3
d) Ben is building steps with blocks. The steps look like the following. How many blocks will it take to build the nth set of steps?	1	2	3
e) Amir walks 3 miles each day as part of an exercise program. At this rate, how many miles will she walk in 10 days?	1	2	3

8. Ms. Kelly was going to draw a picture of on the blackboard. She asked how many circles she should draw to start, and to her surprise her students made different proposals.

Asa: I would draw four circles because the denominator tells you what the whole is.

José: I was thinking that fractions mean divide, and three circles is the whole thing. I would start with three circles, then divide them up.

Mina: I would draw one circle. One is the whole, and you break the whole up into four parts.

Ms. Kelly had planned to draw one circle, but now she was unsure. Which of these students is using a correct interpretation of fractions? (Circle ONE answer.)

a) Only Asa.

b) Only José.

c) Only Mina.

d) Both Asa and Mina, but not José.

e) Asa, José, and Mina.

9. Ms. Marcos’ class was learning that in geometry there are often special cases, so that things may be true sometimes, but false other times. For each of the following statements, indicate whether it is always true, sometimes true, or never true. (Mark ALWAYS TRUE, SOMETIMES TRUE, NEVER TRUE, or I’M NOT SURE for each statement.)

	Always true	Sometimes true	Never true	I’m not sure
Triangles have three acute angles (acute angles are less than 90 degrees).	1	2	3	4
A rectangle is a square.	1	2	3	4
The area of a circle divided by the square of its radius is a little more than 3.	1	2	3	4
If a polygon has all its vertices on a circle, the area of the polygon is less than the area of the circle.	1	2	3	4

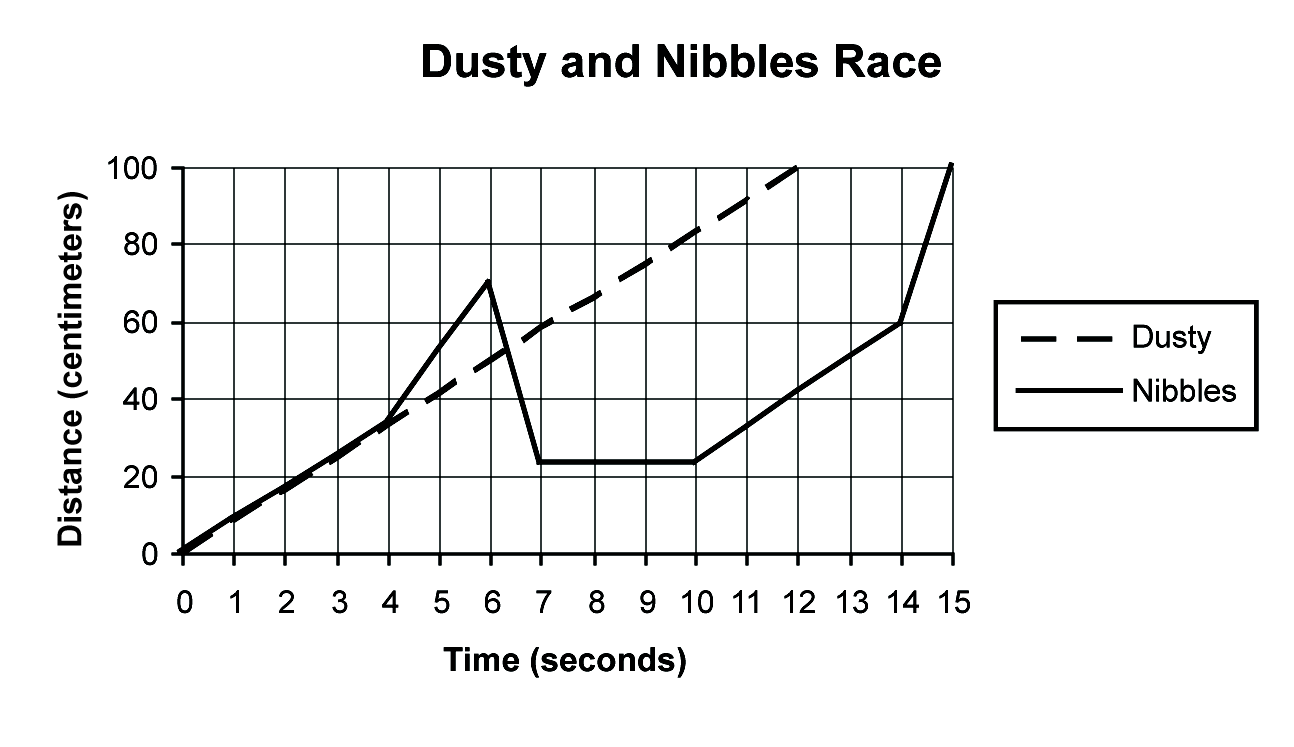
10. Ms. Zeller gave her students the following problem.

The two class hamsters, Dusty and Nibbles, are racing. Describe what happens over the course of the race.

Which of the students’ statements are consistent with the data as shown? (Circle CONSISTENT, INCONSISTENT, or I’M NOT SURE for each.)

	Consistent	Inconsis-tent	I’m not sure
Nibbles runs the same speed as Dusty for a while, and then Nibbles goes faster. She then starts going very slowly until finally she stops for 3 seconds. Then she goes fast again. Finally, she goes even faster at the end, but Dusty has already won.	1	2	3
Dusty is running at a constant speed. Nibbles runs at the same speed for awhile. Then she runs slowly up a slight incline. She realizes that this is not the right place to run, and she turns around and runs back to the correct path. She stops for a moment to brush her whiskers, and then runs toward the finish line. Dusty wins by about 3 seconds.	1	2	3
Nibbles and Dusty start out running the same speed. At about 4 seconds, Nibbles takes off going much faster. Suddenly, she dashes back about 40 cm, stops for 3 seconds, and then takes off again for the finish line. Soon after Dusty has finished the race, she picks up speed again and comes in 3 seconds after Dusty.	1	2	3

11. Mr. Jones decided to use a series of toothpick problems to work on patterns with his students. He started with this one:

A row of squares can be made from toothpicks as follows:

How many toothpicks would be needed to create a similar row of 37 squares?

To check himself, he tried it out. Which answer should he have gotten?

(Circle ONE answer.)

1. 112

2. 113

3. 148

4. None of the above

12. Imagine that you are working with your class on subtracting large numbers. Among your students’ papers, you notice that some have displayed their work in the following ways:

Which of these students is using a method that could be used to subtract any two whole numbers? (Mark ONE answer.)

1. A only

2. B only

3. A and B

4. B and C

5. A, B, and C

6. I’m not sure.

13. Ms. Lewis’ class has been working with geoboards (a square grid of pegs at one unit intervals) to find areas and perimeters of polygons. One of the students, Emilio, creates the following example of a square:

Ms. Lewis asks her class to generate strategies for calculating the area of Emilio’s example. Which of the following are mathematically acceptable? (For each strategy mark YES, NO or I’M NOT SURE.)

	Yes	No	I’m not sure
Use the Pythagorean theorem to find the length of one edge, and then square this number.	1	2	3
Count the number of points inside the square.	1	2	3
Draw a larger square of side length 4 around the square and subtract the areas of the four right triangles with legs of lengths 1 and 3 from the area of the larger square.	1	2	3
This square is a 3.5 by 3.5 that has been rotated, so the area is 3.5 squared.	1	2	3

14. Mr. Nager writes the following statement on the board:

The length and width of a rectangular swimming pool are each doubled, while the depth remains the same.

He asks his students to make mathematical statements about this pool. Which of the following student claims is true? (Mark ONE answer.)

1. It takes twice as much paint to paint the bottom.

2. It takes twice as much paint to paint the four walls.

3. It takes twice as much water to fill the pool.

4. All of the above.

5. None of the above.

6. I’m not sure.

15. Ms. Ashton was teaching her students to represent situations with algebra. She wanted to create a story or context that would be appropriately modeled by the equation y = 2x + 3.

Of the following stories, which would be appropriately modeled by the equation

y = 2x + 3, where x = 1, 2, 3, …? (For each item below, circle YES, NO or I’M NOT SURE.)

	Yes	No	I’m not sure
Lu and her friends want to make birthday cards. They make 3 cards in September. Each month after that they make twice as many cards as the month before. How many cards have they made at the end of x months?
Joaquin earns $2.00 for each magazine he sells. Each time he sells a magazine he also gets a three-dollar tip. How much money will he earn after selling x magazines?
Earl starts with 3 baseball cards. Each week he gets 2 more baseball cards. How many cards does he have at the end of x weeks?

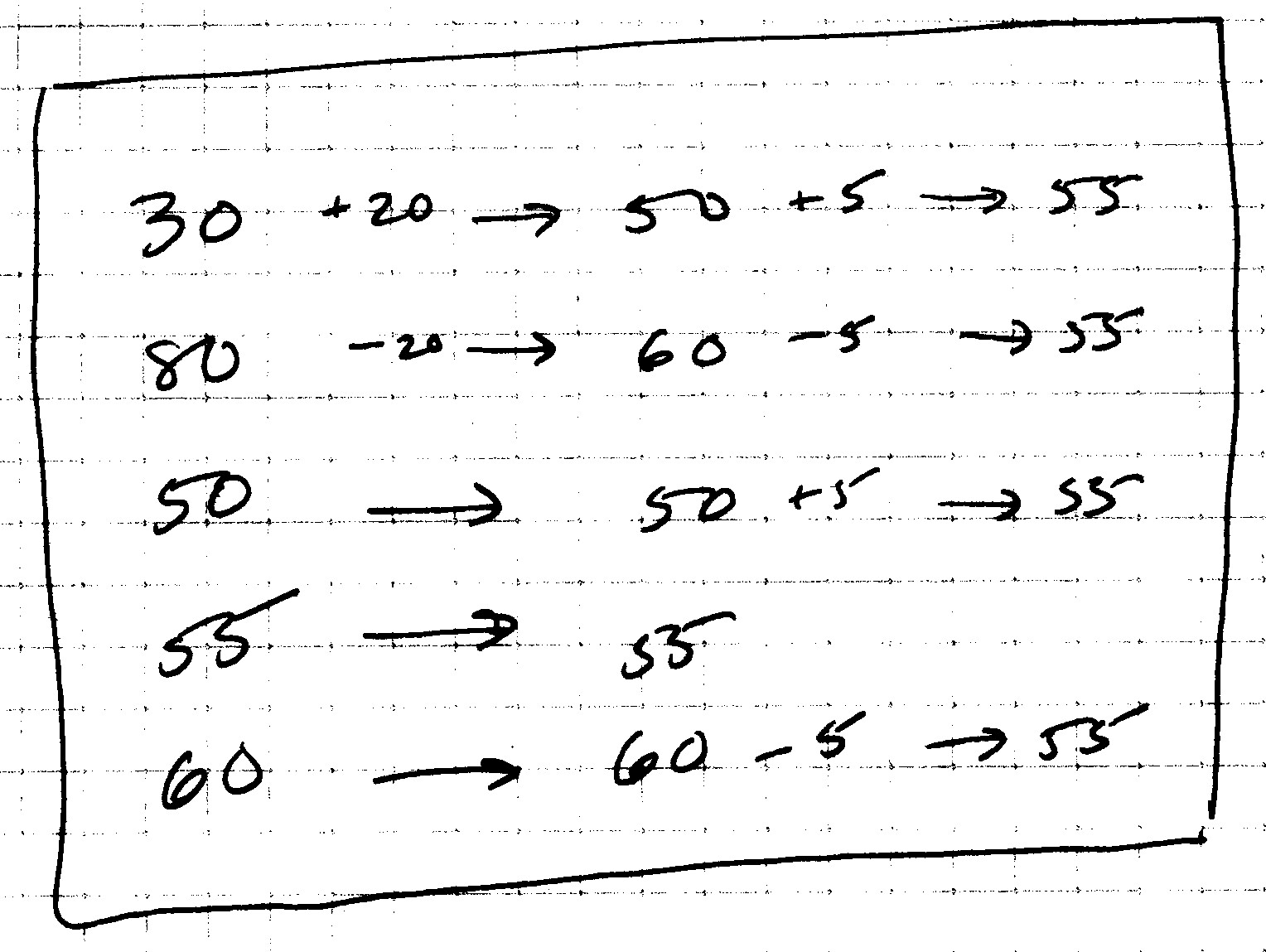
16. Carmen, a health-care worker, works different amounts of hours at different facilities. At last count, she had worked 30, 80, 50, 55, and 60 hours at the various locations and wanted to find the mean (average) hours she had worked at a facility. She used six different ways to figure it out and each time she came up with 55 for an answer. For each of her methods described below, decide whether it will work to find the mean for any group of amounts.

	Yes	No	Not sure
a) Take the smallest and the largest amounts, add them together and divide that in half to get the mean.
b) Even out the amounts with addition and subtraction. That will get you to the mean
c) Arrange the amounts in order from smallest to largest; the amount in the middle will be the mean.
d) Separate the original set of amounts into smaller groups and find the means of the small groups. Add the means that you found and divide by the number of groups you had. This will be the mean of the set of the original amounts.
e) Add all the amounts together and then divide by the number of amounts you added. That is the mean.
f) Draw a bar graph with each of the amounts as a bar. Take some amount from the higher bars and redistribute this amount to the lower bars until all the bars are the same height. This is the mean.

©Learning Mathematics for Teaching 2009. Mathematical knowledge for teaching measures: Patterns, Functions, and Algebra; Geometry; Numbers and Operations; Data, Probability and Statistics. Ann Arbor, MI: Authors.

Paperwork Burden Statement

According to the Paperwork reduction Act of 1995, no persons are required to respond to a collection of information unless such collection displays a valid OMB control number. The valid OMB control number for this information collection is 1830-XXXX. The time required to complete this information collection is estimated to average 20 minutes per response, including the time to review instructions, and complete the items. If you have any comments concerning the accuracy of the time estimate(s) or suggestions for improving this form, please write to: U.S. Department of Education, Washington, D.C. 20202-4537. If you have comments or concerns regarding the status of your individual submission of this form, write directly to: U.S. Department of Education, _____________________Division, _________________ Unit, 400 Maryland Avenue, S.W., PCP Room _________, Washington D.C. 20202-2800.